Решение. 1. Расстояние  между точками
между точками 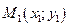 и
и  определяется по формуле:
определяется по формуле:
 . (1)
. (1)
Подставив в эту формулу координаты точек А и В, имеем:
 .
.
2. Уравнение прямой, проходящей через точки 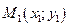 и
и  , имеет вид:
, имеет вид:
 . (2)
. (2)
Подставив в (2) координаты точек:

Для нахождение углового коэффициента  прямой АВ разрешим полученное уравнение относительно у:
прямой АВ разрешим полученное уравнение относительно у:  . Отсюда
. Отсюда  . Подставив в формулу (2) координаты точек А и С, получим уравнение прямой АС.
. Подставив в формулу (2) координаты точек А и С, получим уравнение прямой АС.

Отсюда 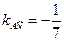 .
.
3. Угол  между двумя прямыми, угловые коэффициенты которых равны
между двумя прямыми, угловые коэффициенты которых равны  и
и  , определяется по формуле:
, определяется по формуле:
 . (3)
. (3)
Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее  ,
,  .
.
 ,
,

4. Так как высота  перпендикулярна стороне
перпендикулярна стороне  , то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.
, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.
 .
.
Уравнение прямой, проходящей через данную точку 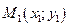 в заданном угловым коэффициентом
в заданном угловым коэффициентом  направлении, имеет вид:
направлении, имеет вид:
 . (4)
. (4)
Подставив в (4) координаты точки С и  , получим уравнение высоты
, получим уравнение высоты  :
:
 . (5)
. (5)
Для нахождения длины  определим координаты точки
определим координаты точки  , решив систему уравнений (АВ) и (
, решив систему уравнений (АВ) и ( ):
):

откуда  , то есть
, то есть 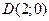 .
.
Подставив в формулу (1) координаты точек С и  , находим:
, находим:
 .
.
5. Уравнение окружности радиуса  с центром в точке
с центром в точке  имеет вид:
имеет вид:
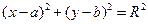 . (6)
. (6)
Так как  является диметром искомой окружности, то ее центр Е есть середина отрезка
является диметром искомой окружности, то ее центр Е есть середина отрезка  . Воспользовавшись формулами деления отрезка пополам, получим:
. Воспользовавшись формулами деления отрезка пополам, получим:

Следовательно,  и
и  . Используя формулу (6), получаем уравнение искомой окружности:
. Используя формулу (6), получаем уравнение искомой окружности: 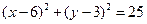 .
.
На рис. 1 в декартовой прямоугольной системе координат  изображен треугольник
изображен треугольник  , высота
, высота  , окружность с центром в точке Е.
, окружность с центром в точке Е.

Задача № 2. 1) Определить тип заданной кривой и построить её (для окружности указать центр, для эллипса и гиперболы – фокусы и эксцентриситет, для параболы – фокус и директрису):
x2+4y2=16.
Решение. Для того, чтобы определить тип кривой второго порядка (окружность, эллипс, гипербола или парабола), произведём преобразования заданного уравнения:

Получили каноническое уравнение эллипса:


– полуоси эллипса.

 Найдём координаты его фокусов: F1(-c;0) и F2(c;0), где – половина расстояния между фокусами.
Найдём координаты его фокусов: F1(-c;0) и F2(c;0), где – половина расстояния между фокусами.
Итак, Тогда F1(-3,5;0) и F2(3,5;0) – фокусы эллипса.
 – эксцентриситет эллипса:
– эксцентриситет эллипса:
Построим эллипс (рис. 2).
 y
y

 • •
• •
-4 F1 F2 4 х
-2
Рис. 2
2). Определить тип заданной кривой и построить её (для окружности указать центр, для эллипса и гиперболы – фокусы и эксцентриситет, для параболы – фокус и директрису):
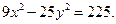
Решение. Преобразуем заданное уравнение:

Получили каноническое уравнение гиперболы:


– полуоси гиперболы.
Найдём координаты её фокусов: F1(-c;0) и F2(c;0), где  – половина расстояния между фокусами.
– половина расстояния между фокусами.
Итак, 
Тогда F1(-5,8;0) и F2(5,8;0) – фокусы гиперболы.
Эксцентриситет гиперболы: 
Построим гиперболу (рис. 3).
 y
y
• •
F1 -5 5 F2 x
-3
Рис. 3.
3). Определить тип заданной кривой и построить её (для окружности указать центр, для эллипса и гиперболы – фокусы и эксцентриситет, для параболы – фокус и директрису).
y2=6x+12
Решение. Преобразуем данное уравнение:

 Получили уравнение параболы:
Получили уравнение параболы: 
Ветви параболы направлены вправо, вершина расположена в точке (x0; y0), т.е. в точке (-2;0).
Для построения параболы её уравнение приведём к простейшему (каноническому) виду. Для этого произведём параллельный перенос системы координат:

Тогда в новой системе координат X′O′Y′, где О′(-2;0) – начало координат, уравнение параболы принимает канонический вид: 
Найдём координаты фокуса и уравнение директрисы:  – фокус,
– фокус,  – уравнение директрисы.
– уравнение директрисы.
Итак, 2p=6, значит, р=3. Тогда F(1,5; 0) и х= -1,5.
Строим параболу в системе координат X′O′Y′ (рис.4).

y
Y′
р
O′ F x(X′)
Рис.4
Задача № 3. Даны координаты трех точек: А(3; 0; –5), В(6; 2; 1), С(12; –12; 3).
Требуется:
1) записать векторы  и
и  в системе орт и найти их модули;
в системе орт и найти их модули;
2) найти угол между векторами  и
и  ;
;
3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору  .
.
Решение. 1) Если даны точки  и
и 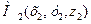 , то вектор
, то вектор  через орты
через орты  выражается следующим образом:
выражается следующим образом:
 .
.
Подставляя в эту формулу координаты точек А и В, имеем:
 .
.
Аналогично
 .
.
Модуль вектора  вычисляется по формуле
вычисляется по формуле
 .
.
Подставляя в формулу найденные ранее координаты векторов  и
и  , находим их модули:
, находим их модули:
 ,
,
 .
.
2) Косинус угла  , образованного векторами
, образованного векторами 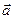 и
и  , равен их скалярному произведению, деленному на произведение их модулей
, равен их скалярному произведению, деленному на произведение их модулей
 .
.
Так как скалярное произведение двух векторов, заданных своими координатами, равно сумме попарных произведений одноименных координат, то
 .
.
Тогда
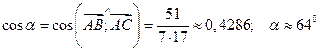 .
.
3) Уравнение плоскости, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  , имеет вид
, имеет вид
 .
.
По условию задачи искомая плоскость проходит через точку  перпендикулярно вектору
перпендикулярно вектору  . Подставляя
. Подставляя 


 , получим:
, получим:

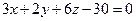 – искомое уравнение плоскости.
– искомое уравнение плоскости.
Задача № 4. Данную систему уравнений решить методом Крамера (с помощью определителей):

Решение. Вычислим определитель системы Δ по правилу «треугольников»:









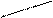




 (a11 a22 a33 + a21 a32 a13+ a12 a23 a31) – (a31 a22 a13+ a32 a23 a11+ a21 a12 a33).
(a11 a22 a33 + a21 a32 a13+ a12 a23 a31) – (a31 a22 a13+ a32 a23 a11+ a21 a12 a33).
Итак,

Δ≠0  система имеет единственное решение, которое находим по формулам Крамера:
система имеет единственное решение, которое находим по формулам Крамера:

Определители  получаем заменой соответствующего столбца определителя Δ столбцом свободных членов системы.
получаем заменой соответствующего столбца определителя Δ столбцом свободных членов системы.
Вычислим определители 


Таким образом, 
Сделаем проверку, подставив найденное решение в каждое уравнение данной системы:
 – верно.
– верно.
Ответ: (3;0;-2).
Задача № 5. Вычислить пределы:
а)  б)
б)  в)
в) 
Решение. а) Подстановка предельного значения аргумента х= -3 приводит к неопределенному выражению вида  .
.
Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель  . Такое сокращение возможно, так как множитель
. Такое сокращение возможно, так как множитель  отличен от нуля при
отличен от нуля при  :
:

б) При х→∞ числитель и знаменатель дроби  стремятся к ∞.
стремятся к ∞.
Тогда получаем неопределённость вида  которая раскрывается по следующему правилу: предел отношения двух бесконечно больших функций, являющихся многочленами, равен пределу отношения их слагаемых со старшей степенью переменной.
которая раскрывается по следующему правилу: предел отношения двух бесконечно больших функций, являющихся многочленами, равен пределу отношения их слагаемых со старшей степенью переменной.

Итак,
в) Для раскрытия неопределённости вида  , содержащей тригонометрические функции, воспользуемся эквивалентными функциями:
, содержащей тригонометрические функции, воспользуемся эквивалентными функциями:
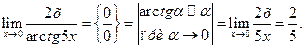
Контрольная работа № 2
Задача № 6. Провести полное исследование функции и построить её график:

Решение. Проведём исследование функции по следующей схеме:
1) Область определения функции: 
2) Возрастание/убывание, экстремумы функции:

Найдём критические точки функции – точки, в которых y'=0 или не существует:


Точек, в которых производная не определена, нет. Отметим полученные точки на числовой прямой:
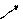


+ – +



-1 3 х
Определим знак производной на каждом интервале: подставим любую точку из интервала в производную y′=x2-2x-3, тогда знак полученного значения производная сохраняет на всём интервале. Например, y′(-2)=(-2)2-2(-2)-3=5>0,
y′(0)=02-2∙0-3=-3<0,
y′(4)=42-2∙4-3=5>0.
Теперь по полученным знакам производной делаем вывод о поведении функции: знак «+» соответствует возрастанию функции, «-» – убыванию. А точки, в которых происходит смена знака, являются точками экстремума функции: хmax= -1, xmin=3. Найдём экстремумы:

Итак, точка  – точка максимума,
– точка максимума,  – точка минимума.
– точка минимума.
3) Найдём интервалы выпуклости/вогнутости и точки перегиба графика функции.




Определим знак второй производной на интервалах (-∞;1) и (1;∞): y"(0)=2∙0-2=-2<0, y"(2)=2∙2-2=2>0. Следовательно, на первом интервале график является выпуклым, на втором – вогнутым, а при х=1 имеет перегиб.
Найдём соответствующее значение функции:
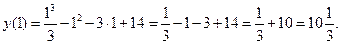
Таким образом, точка  – точка перегиба графика функции.
– точка перегиба графика функции.
Теперь, пользуясь результатами исследования функции, строим её график (рис. 5).
 Рис. 5
Рис. 5
Задача № 7. Найти дифференциал указанной функции.

Решение. Преобразуем функцию, применяя свойства степеней:


Затем, применяя правила дифференцирования и табличные формулы, получаем:

Дифференциал функции равен произведению её производной на дифференциал независимой переменной:  Тогда для данной функции:
Тогда для данной функции:
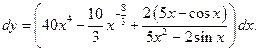
Задача № 8. Исследовать на экстремум функцию  .
.
Решение. Находим стационарные точки – точки, в которых частные производные функции равны нулю:

Решение последней системы дает четыре стационарные точки:
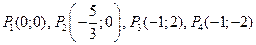 .
.
Находим частные производные второго порядка:
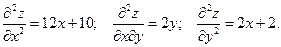
Исследуем каждую стационарную точку.
1) В точке  Так как
Так как 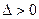 и
и  , то в этой точке функция имеет минимум.
, то в этой точке функция имеет минимум.

2) В точке  Так как
Так как 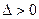 и
и  , то в этой точке функция имеет максимум.
, то в этой точке функция имеет максимум.

3) В точке  Так как
Так как 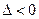 , то в этой точке нет экстремума.
, то в этой точке нет экстремума.
4) В точке  Так как
Так как 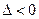 , то в этой точке нет экстремума.
, то в этой точке нет экстремума.
Задача № 9. Вычислить площадь фигуры, ограниченной линиями  ,
,  .
.
Решение. Графиком первой функции является парабола с ветвями вверх, второй функции – прямая.
Найдём координаты вершины параболы:
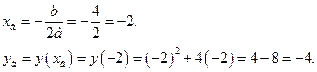
Итак, точка (-2;-4) является вершиной параболы.
Для нахождения точек пересечения данных линий решим систему уравнений:

Найдём вторые координаты (ординаты) точек пересечения графиков, подставив найденные значения х в любое из уравнений: y(-4)=-4+4=0, y(1)=1+4=5. Таким образом, парабола и прямая пересекаются в точках (-4;0) и (1;5).
Теперь вершину параболы и точки пересечения используем для построения графиков (рис. 6).

Рис. 6
Площадь фигуры, ограниченной сверху и снизу непрерывными линиями  и
и 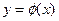 , пересекающимися в точках с абсциссами x=a и x=b, определяется по формуле:
, пересекающимися в точках с абсциссами x=a и x=b, определяется по формуле:
 .
.
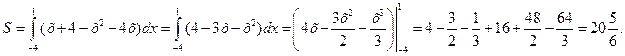
Задача № 10. Найти общее решение дифференциального уравнения 1-го порядка.

Решение. Это дифференциальное уравнение 1-го порядка с разделяющимися переменными. Находим его решение по стандартной схеме:

Разделим переменные:
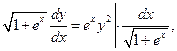

Проинтегрируем обе части уравнения:

Второй интеграл решим методом замены переменной:

Теперь приравняем результаты, причём произвольную постоянную С запишем только в правой части:

 – общее решение.
– общее решение.
Задача № 11. Найти частное решение дифференциального уравнения 2-го порядка, удовлетворяющее указанным начальным условиям.

Решение. Это линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Общее решение уравнения составляется в зависимости от корней характеристического уравнения:

Если корни характеристического уравнения действительны и различны, то общее решение имеет вид: 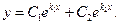 В нашем случае
В нашем случае  значит,
значит, 
Теперь из общего решения уравнения выделим частное решение, удовлетворяющее заданным начальным условиям.




Итак, 
Подставим найденные значения констант в общее решение. Тогда  – частное решение уравнения.
– частное решение уравнения.
Задача 12. Дан степенной ряд  . Написать первые три члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
. Написать первые три члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
Решение.  – общий член ряда. Подставив в эту формулу вместо n значения 1, 2, 3, …, можно найти любой член ряда:
– общий член ряда. Подставив в эту формулу вместо n значения 1, 2, 3, …, можно найти любой член ряда:

Степенной ряд в общем виде записывается следующим образом:  где an – формула числовых коэффициентов. Для данного ряда
где an – формула числовых коэффициентов. Для данного ряда 
Областью сходимости степенного ряда является интервал (-R;R), где  – радиус сходимости. Вычислим его:
– радиус сходимости. Вычислим его:


 Итак, ряд является сходящимся (абсолютно) при всех х, принадлежащих интервалу
Итак, ряд является сходящимся (абсолютно) при всех х, принадлежащих интервалу 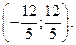
Теперь проверим сходимость ряда на концах этого интервала.
Пусть 
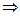 получаем ряд:
получаем ряд: 
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница:


 ряд сходится, значит,
ряд сходится, значит,  – точка сходимости.
– точка сходимости.
При  исходный ряд принимает вид:
исходный ряд принимает вид:  – числовой знакоположительный ряд. Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
– числовой знакоположительный ряд. Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:  Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит,
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит,  – точка расходимости.
– точка расходимости.
Таким образом, данный степенной ряд является сходящимся при 






