МАТЕМАТИКА
Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой его учебного шифра. При этом если предпоследняя цифра его учебного шифра есть число нечётное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1. Если предпоследняя цифра учебного шифра есть число (0, 2, 4, 6, 8), то номера задач даны в таблице 2.
Таблица № 1.
| Номер варианта | Номера задач для контрольных работ | ||
| КР № 1 | КР № 2 | КР № 3 | |
| 1.1, 2.1, 3.1, 4.1, 5.1 | 6.1, 7.1, 8.1, 9.1, 10.1, 11.1, 12.1 | 13.1, 14.1, 15.1, 16.1, 17.1, 18,1 | |
| 1.2, 2.2, 3.2, 4.2, 5.2 | 6.2, 7.2, 8.2, 9.2, 10.2, 11.2, 12.2 | 13.2, 14.2, 15.2, 16.2, 17.2, 18.2 | |
| 1.3, 2.3, 3.3, 4.3, 5.3 | 6.3, 7.3, 8.3, 9.3, 10.3, 11.3, 12.3 | 13.3, 14.3, 15.3, 16.3, 17.3, 18.3 | |
| 1.4, 2.4, 3.4, 4.4, 5.4 | 6.4, 7.4, 8.4, 9.4, 10.4, 11.4, 12.4 | 13.4, 14.4, 15.4, 16.4, 17.4, 18.4 | |
| 1.5, 2.5, 3.5, 4.5, 5.5 | 6.5, 7.5, 8.5, 9.5, 10.5, 11.5, 12.5 | 13.5, 14.5, 15.5, 16.5, 17.5, 18.5 | |
| 1.6, 2.6, 3.6, 4.6, 5.6 | 6.6, 7.6, 8.6, 9.6, 10.6, 11.6, 12.6 | 13.6, 14.6, 15.6, 16.6, 17.6, 18.6 | |
| 1.7, 2.7, 3.7, 4.7, 5.7 | 6.7, 7.7, 8.7, 9.7, 10.7, 11.7, 12.7 | 13.7, 14.7, 15.7, 16.7, 17.7, 18.7 | |
| 1.8, 2.8, 3.8, 4.8, 5.8 | 6.8, 7.8, 8.8, 9.8, 10.8, 11.8, 12.8 | 13.8, 14.8, 15.8, 16.8, 17.8, 18.8 | |
| 1.9, 2.9, 3.9, 4.9, 5.9 | 6.9, 7.9, 8.9, 9.9, 10.9, 11.9, 12.9 | 13.9, 14.9, 15.9, 16.9, 17.9, 18.9 | |
| 1.10, 2.10, 3.10, 4.10, 5.10 | 6.10, 7.10, 8.10, 9.10, 10.10, 11.10, 12.10 | 13.10, 14.10, 15.10, 16.10, 17.10, 18.10 |
Таблица № 2.
| Номер варианта | Номера задач для контрольных работ | ||
| КР № 1 | КР № 2 | КР № 3 | |
| 1.11, 2.11, 3.11, 4.11, 5.11 | 6.11, 7.11, 8.11, 9.11, 10.11, 11.11, 12.11 | 13.11, 14.11, 15.11, 16.11, 17.11, 18.1 | |
| 1.12, 2.12, 3.12, 4.12, 5.12 | 6.12, 7.12, 8.12, 9.12, 10.12, 11.12, 12.12 | 13.12, 14.12, 15.12, 16.12, 17.12, 18.2 | |
| 1.13, 2.13, 3.13, 4.13, 5.13 | 6.13, 7.13, 8.13, 9.13, 10.13, 11.13, 12.13 | 13.13, 14.13, 15.13, 16.13, 17.13, 18.3 | |
| 1.14, 2.14, 3.14, 4.14, 5.14 | 6.14, 7.14, 8.14, 9.14, 10.14, 11.14, 12.14 | 13.14, 14.14, 15.13, 16.13, 17.13, 18.4 | |
| 1.15, 2.15, 3.15, 4.15, 5.15 | 6.15, 7.15, 8.15, 9.15, 10.15, 11.15, 12.15 | 13.15, 14.15, 15.15, 16.15, 17.15, 18.5 | |
| 1.16, 2.16, 3.16, 4.16, 5.16 | 6.16, 7.16, 8.16, 9.16, 10.16, 11.16, 12.16 | 13.16, 14.16, 15.16, 16.16, 17.16, 18.6 | |
| 1.17, 2.17, 3.17, 4.17, 5.17 | 6.17, 7.17, 8.17, 9.17, 10.17, 11.17, 12.17 | 13.17, 14.17, 15.17, 16.17, 17.17, 18.7 | |
| 1.18, 2.18, 3.18, 4.18, 5.18 | 6.18, 7.18, 8.18, 9.18, 10.18, 11.18, 12.18 | 13.18, 14.18, 15.18, 16.18, 17.18, 18.8 | |
| 1.19, 2.19, 3.19, 4.19, 5.19 | 6.19, 7.19, 8.19, 9.19, 10.19, 11.19, 12.19 | 13.19, 14.19, 15.19, 16.19, 17.19, 18.9 | |
| 1.20, 2.20, 3.20, 4.20, 5.20 | 6.20, 7.20, 8.20, 9.20, 10.20, 11.20, 12.20 | 13.20, 14.20, 15.20, 16.20, 17.20, 18.10 |
Контрольная работа №1
1. Даны вершины треугольника ABC. Найти:
Длину стороны AB;
2) уравнения сторон АВ и АС и их угловые коэффициенты;
3) угол А;
4) уравнение высоты СD и её длину;
5) уравнение окружности, для которой высота СD является диаметром.
А(–5; 0), В(7; 9), С(5; –5).
А(–7; 2), В(5; 11), С(3; –3).
А(–5; –3), В(7; 6), С(5; –8).
1.4. А(–6; –2), В(6; 7), С(4; –7).
1.5. А(–8; –4), В(4; 5), С(2; –9).
1.6. А(0; –1), В(12; 8), С(10; –6).
1.7. А(–6; 1), В(6; 10), С(4; –4).
1.8. А(–2; –4), В(10; 5), С(8; –9).
1.9. А(–3; 0), В(9; 9), С(7; –5).
1.10. А(–9; –2), В(3; 7), С(1; –7).
1.11. А(–5; 2), В(7; –7), С(5; 7).
1.12. А(–7; 5), В(5; –4), С(3; 10).
1.13. А(–7; 1), (5; –8), С(3; 6).
1.14. А(0; 3), В (12; –6), С(10; 8).
1.15. А (–8; 4), В (4; –5), С (2; 9).
1.16. А (–2; 2), В (10; –7), С (8; 7).
1.17. А (1; 2), В (13; –7), С (11; 7).
1.18. А (–4; 1), В (8; –8), С (6; 6).
1.19. А (–7; –1), В (5; –10), С (3; 4).
1.20. А (–3; 3), В (9; –6), С (7; 8).
2. Oпределить тип заданной кривой и построить её (для окружности указать центр, для эллипса и гиперболы – фокусы и эксцентриситет, для параболы – фокус и директрису).
2.1. 4x2+25y2=100. 2.2. x2+y2–4x+2y–4 = 0.
2.3. y2=2x+2. 2.4. 9x2–16y2=144.
2.5. x2=–2y+2. 2.6. 16x2+25y2=400.
2.7. x2+y2+2x–4y–4=0. 2.8. y2=–4x+4.
2.9. 16x2–9y2=144. 2.10. x2=4y+4.
2.11. x2+4y2=64. 2.12. x2+y2+4x–6y+9 = 0.
2.13. y2=2x+6. 2.14. 4x2–y2=64.
2.15. x2=–4y+12. 2.16. x2+9y2=36.
2.17. x2+y2–6x+4y+4=0. 2.18. y2=6x–12.
2.19. 16x2–25y2=400. 2.20. x2=–2y+6.
3. Даны координаты точек А, В, С. Требуется:
1) записать векторы  и
и  в системе орт и найти их модули;
в системе орт и найти их модули;
2) найти угол между векторами  и
и 
3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору  .
.
3.1. А(7; –4; 1), В(12; –3; 1), С(10; 1; 5).
3.2. А(0; –3; 3), В(5; –2; 3), С(3; 2; 7).
3.3. А(–2; –1; –2), В(3; 0; –2), С(1; 4; 2).
3.4. А(–6; 0; 0), В(–1; 1; 0), С(–3; 5; 4).
3.5. А(–2; –3; –8), В(3; –2; –8), С(1; 2; –4).
3.6. А(1; 0; –1), В(6; 1; –1), С(4; 5; 3).
3.7. А(–1; 4; 1), В(4; 5; 1), С(2; 9; 5).
3.8. А(3; –6; –3), В(8; –5; –3), С(6; –1; 1).
3.9. А(1; 0; 0), В(6; 1; 0), С(4; 5; 4).
3.10. А(2; –8; –2), В(7; –7; –2), С(5; –3; 2).
3.11. А(2; –3; 1), В(10; –5; 3), С(11; -1; 4).
3.12. А(–6; 1; 5), В(2; 3; –5), С(1; 0; 4).
3.13. А(1; –2; –3), В(6; 8; –1), С(5; 2; 1).
3.14. А(–5; 1; 3), В(–2; 0; 5), С(–4; 1; 3).
3.15. А(–3; –1; –6), В(5; –4; –2), С(0; 1; –3).
3.16. А(7; 6; –2), В(4; 3; –2), С(2; 9; 1).
3.17. А(–3; 5; 2), В(9; 2; 3), С(1; 0; 4).
3.18. А(2; –2; –1), В(7; –6; –1), С(5; –2; 6).
3.19. А(5; 2; 0), В(3; 0; 1), С(7; 2; 3).
3.20. А(5; –2; –6), В(4; –6; –1), С(5; –2; 6).
4. Решить систему уравнений методом Крамера (с помощью определителей).
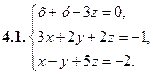




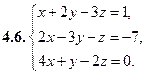













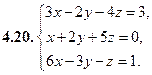
5. Найти указанные пределы.
5.1. а)  ; б)
; б)  ; в)
; в)  .
.
5.2. а)  ; б)
; б)  ; в)
; в) 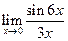 .
.
5.3. а)  ; б)
; б) 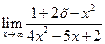 ; в)
; в)  .
.
5.4. а)  ; б)
; б)  ; в)
; в)  .
.
5.5. а)  ; б)
; б)  ; в)
; в)  .
.
5.6. а) 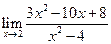 ; б)
; б) 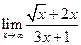 ; в)
; в)  .
.
5.7. а)  ; б)
; б) 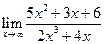 ; в)
; в) 
5.8. а) 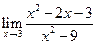 ; б)
; б)  ; в)
; в)  .
.
5.9. а)  ; б)
; б)  ; в)
; в)  .
.
5.10. а)  ; б)
; б)  ; в)
; в)  .
.
5.11. а)  ; б)
; б)  ; в)
; в)  .
.
5.12. а)  ; б)
; б)  ; в)
; в)  .
.
5.13. а)  ; б)
; б)  ; в)
; в)  .
.
5.14. а)  ; б)
; б) 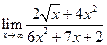 ; в)
; в) 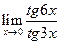 .
.
5.15. а) 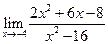 ; б)
; б)  ; в)
; в)  .
.
5.16. а) 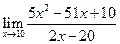 ; б)
; б)  ; в)
; в) 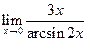 .
.
5.17. а)  ; б)
; б) 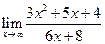 ; в)
; в)  .
.
5.18. а)  ; б)
; б)  ; в)
; в) 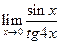 .
.
5.19. а)  ; б)
; б)  ; в)
; в)  .
.
5.20. а)  ; б)
; б) 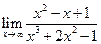 ; в)
; в) 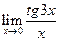 .
.
Контрольная работа № 2
6. Провести полное исследование заданной функции и построить её график.
6.1.  6.2.
6.2. 
6.3.  6.4.
6.4. 
6.5.  6.6.
6.6. 
6.7. 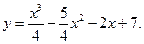 6.8.
6.8. 
6.9. 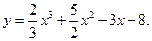 6.10.
6.10. 
6.11.  6.12.
6.12. 
6.13.  6.14.
6.14. 
6.15. 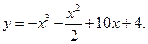 6.16.
6.16. 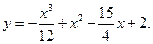
6.17.  6.18.
6.18. 
6.19. 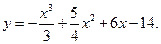 6.20.
6.20. 
7. Найти дифференциал указанной функции.
7.1.  7.2.
7.2. 
7.3.  7.4.
7.4. 
7.5.  7.6.
7.6. 
7.7.  7.8.
7.8. 
7.9.  7.10.
7.10. 
7.11.  7.12.
7.12. 
7.13.  7.14.
7.14. 
7.15.  7.16.
7.16. 
7.17.  7.18.
7.18. 
7.19.  7.20.
7.20. 
8. Исследовать на экстремум функцию  .
.
8.1.  . 8.2.
. 8.2.  .
.
8.3.  . 8.4.
. 8.4.  .
.
8.5.  . 8.6.
. 8.6. 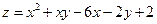 .
.
8.7.  . 8.8.
. 8.8.  .
.
8.9.  . 8.10.
. 8.10.  .
.
8.11. 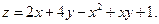 8.12.
8.12. 
8.13.  8.14.
8.14. 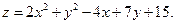
8.15.  8.16.
8.16. 
8.17.  8.18.
8.18. 
8.19.  8.20.
8.20. 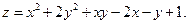
9. Вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
9.1.. 9.2..
9.3.. 9.4..
9.5.. 9.6..
9.7.. 9.8..
9.9.. 9.10..
9.11.  9.12.
9.12. 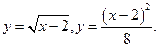
9.13.  9.14.
9.14. 
9.15.  9.16.
9.16. 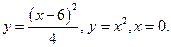
9.17.  9.18.
9.18. 
9.19.  9.20.
9.20. 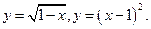
10. Найти общее решение дифференциального уравнения первого порядка.
10.1.. 10.2..
10.3.. 10.4..
10.5.. 10.6..
10.7.. 10.8..
10.9.. 190..
10.11.  10.12.
10.12. 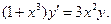
10.13.  10.14.
10.14. 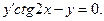
10.15.  10.16.
10.16. 
10.17.  10.18.
10.18. 
10.19.  10.20.
10.20. 
11. Найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям.
11.1. 
11.2. 
11.3. 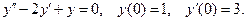
11.4. 
11.5. 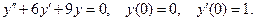
11.6. 
11.7. 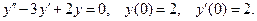
11.8. 
11.9. 
11.10. 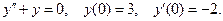
11.11. 
11.12. 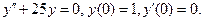
11.13. 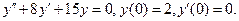
11.14. 
11.15. 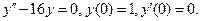
11.16. 
11.17. 
11.18. 
11.19. 
11.20. 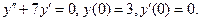
12. Дан степенной ряд 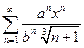 . При заданных значениях a и b написать первые три члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
. При заданных значениях a и b написать первые три члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
12.1. 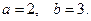 12.2.
12.2. 
12.3.  12.4.
12.4. 
12.5.  12.6.
12.6. 
12.7. 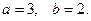 12.8.
12.8. 
12.9.  12.10.
12.10. 
12.11. 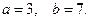 12.12.
12.12. 
12.13.  12.14.
12.14. 
12.15.  12.16.
12.16. 
12.17. 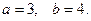 12.18.
12.18. 
12.19.  12.20.
12.20. 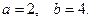
Контрольная работа № 3
13.1. В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в мягком переплете. Библиотекарь взял два учебника. Найти вероятность того, что оба учебника окажутся в мягком переплете.
13.2. Студент знает ответы на 20 из 25 вопросов программы. Найти вероятность того, что он знает ответы на предложенные ему экзаменатором три вопроса.
13.3. Для некоторой местности в июле шесть пасмурных дней. Найти вероятность того, что первого и второго июля будет ясная погода.
13.4. Из 200 рабочих норму выработки не выполняют 15 человек. Найти вероятность того, что два случайно выбранных рабочих не выполняют норму.
13.5. В ящике лежат 20 электрических лампочек, из которых 2 нестандартные. Найти вероятность того, что взятые одна за другой две лампочки окажутся стандартными.
13.6. В урне 8 белых и 7 чёрных шаров. Наудачу взяли два шара. Какова вероятность, что они оба чёрные?
13.7. Из колоды в 36 карт извлекаются наудачу 4 карты. Какова вероятность того, что все карты бубновой масти?
13.8. Одновременно подбрасываются две игральные кости. Какова вероятность того, что сумма выпавших очков равна 10?
13.9. Студент знает первый вопрос на 95 %, второй – на 50 %, третий – лишь на 20 %. Какова вероятность получения зачёта студентом, если для этого достаточно ответить хотя бы на один вопрос?
13.10. Три стрелка стреляют по мишени. Вероятность попадания в цель первым стрелком равна 0,6, вторым – 0,7, третьим – 0,8. Найти вероятность того, что при одном выстреле попадут в цель: а) все три стрелка; б) хотя бы один из них.
13.11. Одновременно бросаются две игральные кости. Найти вероятность того, что на каждой кости появится нечетное количество очков.
13.12. Из заготовленной для посева пшеницы зерно первого сорта составляет 40%, второго сорта – 50%, третьего сорта – 10%. Вероятность того, что взойдет зерно первого сорта равна 0,8, второго – 0,5, третьего – 0,3. Найти вероятность того, что взойдет наугад взятое зерно.
13.13. В магазин поступили телевизоры из трех заводов. Вероятность того, что телевизор изготовлен на первом заводе, равна 0,3, на втором – 0,2, на третьем – 0,5. Вероятность того, что телевизор окажется бракованным, для первого завода равна 0,01, для второго – 0,02, для третьего – 0,03. Найти вероятность того, что наугад взятый телевизор окажется небракованным.
13.14. В мастерской на трех станках изготавливаются однотипные детали. При этом первый станок изготавливает половину всех деталей, второй – 40 %, и третий – 10 %. Вероятность изготовления бракованной детали на первом станке равна 0,01, на втором – 0,03, на третьем – 0,05. Найти вероятность того, что наугад выбранная деталь окажется стандартной.
13.15. Вероятность попадания в цель при одном выстреле равна 0,7. Производится 4 выстрела. Найти вероятность того, что цель будет поражена: а) три раза; б) не более двух раз.
13.16. Вероятность всхожести пшеницы равна 0,8. Какова вероятность того, что из 5 семян взойдет не менее 3-х?
13.17. Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность того, что при 5 выстрелах будет не менее 3-х попаданий.
13.18. Всхожесть семян пшеницы составляет 90 %. Определить наиболее вероятное число всходов из 200 посеянных семян.
13.19. Семена пшеницы содержат 0,2 % сорняков. Найти вероятность того, что в 1000 семян будет 6 семян сорняков.
13.20. Вероятность ошибки при наборе текста равна 0,004. Найти вероятность того, что при наборе 500 знаков будет сделано 3 ошибки.
14. Дана вероятность р того, что семя злака прорастёт. Найти вероятность того, что из п посеянных семян прорастёт ровно  семян.
семян.
14.1. n=900, p=0,1, k=95. 14.6. n=400, p=0,6, k=250.
14.2. n=800, p=0,2, k=150. 14.7. n=300, p=0,7, k=200.
14.3. n=700, p=0,3, k=220. 14.8. n=200, p=0,8, k=150.
14.4. n=600, p=0,4, k=250. 14.9. n=100, p=0,9, k=85.
14.5. n=500, p=0,5, k=240. 14.10. n=50, p=0,1, k=7.
Дана вероятность р появления события А в каждом из п независимых испытаний. Найти вероятность того, что в этих испытаниях событие А появится не менее  раз и не более
раз и не более  раз.
раз.
14.11. n=50, p=0,9, k1=35, k2=46. 14.16. n=550, p=0,4, k1=210, k2=250.
14.12. n=150, p=0,8, k1=100, k2=130. 14.17. n=650, p=0,3, k1=180, k2=200.
14.13. n=250, p=0,7, k1=150, k2=180. 14.18. n=750, p=0,4, k1=290, k2=340.
14.14. n=350, p=0,6, k1=200, k2=240. 14.19. n=850, p=0,5, k1=400, k2=480.
14.15. n=450, p=0,5, k1=200, k2=230. 14.20. n=950, p=0,6, k1=550, k2=630.
15. Задан закон распределения дискретной случайной величины Х (в первой строке указаны возможные значения величины Х, во второй строке даны вероятности р этих значений). Найти: 1) математическое ожидание M(X); 2) дисперсию D(X); 3) среднее квадратическое отклонение σ(X).
| 15.1. | Х | ||||
| Р | 0,1 | 0,3 | 0,2 | 0,4 |
| 15.11. | Х | ||||
| Р | 0,1 | 0,3 | 0,2 | 0,4 |
| 15.2. | Х | ||||
| Р | 0,1 | 0,3 | 0,4 | 0,2 |
| 15.12. | Х | ||||
| Р | 0,2 | 0,1 | 0,3 | 0,4 |
| 15.3. | Х | ||||
| Р | 0,1 | 0,3 | 0,2 | 0,4 |
| 15.13. | Х | ||||
| Р | 0,1 | 0,3 | 0,2 | 0,4 |
| 15.4. | Х | ||||
| Р | 0,3 | 0,3 | 0,2 | 0,2 |
| 15.14. | Х | ||||
| Р | 0,1 | 0,3 | 0,4 | 0,2 |
| 15.5. | Х | ||||
| Р | 0,1 | 0,3 | 0,2 | 0,4 |
| 15.15. | Х | ||||
| Р | 0,3 | 0,3 | 0,2 | 0,2 |
| 15.6. | Х | ||||
| Р | 0,2 | 0,5 | 0,2 | 0,1 |
| 15.16. | Х | ||||
| Р | 0,2 | 0,5 | 0,2 | 0,1 |
| 15.7. | Х | ||||
| Р | 0,1 | 0,4 | 0,3 | 0,2 |
| 15.17. | Х | ||||
| Р | 0,1 | 0,4 | 0,3 | 0,2 |
| 15.8. | Х | ||||
| Р | 0,5 | 0,2 | 0,2 | 0,1 |
| 15.18. | Х | ||||
| Р | 0,5 | 0,2 | 0,2 | 0,1 |
| 15.9. | Х | ||||
| Р | 0,2 | 0,4 | 0,3 | 0,1 |
| 15.19. | Х | ||||
| Р | 0,2 | 0,4 | 0,3 | 0,1 |
| 15.10. | Х | ||||
| Р | 0,3 | 0,2 | 0,2 | 0,3 |
| 15.20. | Х | ||||
| Р | 0,3 | 0,2 | 0,2 | 0,3 |
16. Случайная величина Х задана функцией распределения F(x). Найти:
1) функцию плотности распределения f(x);
2) математическое ожидание M(X);
3) дисперсию D(X).
16.1.  16.9.
16.9. 
16.2.  16.10.
16.10. 
16.3.  16.11.
16.11. 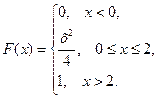
16.4.  16.12.
16.12. 
16.5. 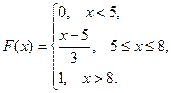 16.13.
16.13. 
16.6. 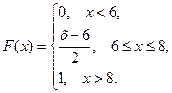 16.14.
16.14. 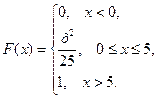
16.7.  16.15.
16.15. 
16.8.  16.16.
16.16. 
16.17.  16.19.
16.19. 
16.18. 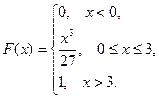 16.20.
16.20. 
17.1. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно 0,25 мм. Стандартными считаются детали, размер которых заключен между 199,5 мм и 200,5 мм. Найти процент стандартных деталей.
17.2. Средний диаметр стволов деревьев на некотором участке равен 25 см, среднее квадратическое отклонение равно 5 см. Считая диаметр ствола случайной величиной, распределенной нормально, найти процент деревьев, имеющих диаметр свыше 20 см.
17.3. Размер плода имеет нормальное распределение со средним значением 16 см и средним квадратическим отклонением 2 см. Найти процент плодов, размер которых находится в пределах от 12 см до 19 см.
17.4. Среднее квадратическое отклонение нормально распределенной случайной величины равно 0,5. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине не превосходит 1.
17.5. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 150 мм и средним квадратическим отклонением 0,5 мм. Найти процент деталей, размер которых отклоняется от среднего менее чем на 0,2 мм.
17.6. Средний вес зерна равен 0,2 г, среднее квадратическое отклонение равно 0,05 г. Определить вероятность того, что вес наудачу взятого зерна окажется в пределах от 0,16 г до 0,22 г.
17.7. Норма высева семян на 1 га равна 200 кг. Фактический расход семян на 1 га имеет нормальное распределение и колеблется около этого значения со средним квадратическим отклонением 10 кг. Найти вероятность того, что расход семян на 1 га будет не более 220 кг.
17.8. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 195 мм, среднее квадратическое отклонение равно 0,35 мм. Найти процент деталей, размер которых менее 195,5 мм.
17.9. Масса яблока, средняя величина которой равна 150 г, является нормально распределенной случайной величиной со средним квадратическим отклонением 20 г. Найти вероятность того, что масса наугад взятого яблока будет заключена в пределах от 130 г до 180 г.
17.10. Масса животного распределена по нормальному закону со средним значением 125 кг и средним квадратическим отклонением 7 кг. Найти процент животных, масса которых отклоняется от средней менее чем на 10 кг.
17.11. Диаметр яблока имеет нормальное распределение со средним значением 7 см и средним квадратическим отклонением 1,5 см. Найти вероятность того, что диаметр наудачу взятого яблока будет заключён в пределах от 6 см до 9 см.
17.12. Рост человека имеет нормальное распределение со средним значением 172 см и средним квадратическим отклонением 9 см. Найти процент людей, рост которых более 180 см.
17.13. Случайная величина имеет нормальное распределение со средним значением 28 и средним квадратическим отклонением 13. Найти процент положительных значений величины.
17.14. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 220 мм и средним квадратическим отклонением 0,4 мм. Найти процент деталей, размер которых отклоняется от среднего менее чем на 0,5 мм.
17.15. Среднее квадратическое отклонение нормально распределенной случайной величины равно 5. Найти вероятность того, что отклонение случайной величины от её математического ожидания по абсолютной величине не превзойдёт 7.
17.16. Масса животного распределена по нормальному закону со средним значением 95 кг и средним квадратическим отклонением 4 кг. Найти процент животных, масса которых заключена в пределах от 80 кг до 100 кг.
17.17. Случайная величина имеет нормальное распределение со средним значением 18 и средним квадратическим отклонением 3. Найти процент значений величины, принадлежащих интервалу (15;20).
17.18. Средняя дневная температура воздуха в июле равна 29º. Найти вероятность того, что в случайно взятый июльский день будет не менее 25º, если температура воздуха имеет нормальное распределение со средним квадратическим отклонением 3º.
17.19. Случайная величина имеет нормальное распределение со средним значением 12 и средним квадратическим отклонением 9. Найти процент положительных значений величины.
17.20. Вес зерна имеет нормальное распределение со средним значением 0,2 г и средним квадратическим отклонением 0,04 г. Найти процент зёрен, вес которых не менее 0,3 г.
18. В ряде задач нужно использовать данные таблицы 1, в которой приведены результаты выборочного социологического обследования 100 городских семей на предмет изучения уровня жизни населения.
Таблица 1. – Данные обследования 100 городских семей
| № | Количество членов в семье | Жилищные условия | Доход семьи в месяц, руб. | Загородный земельный участок | Автомобиль | Гараж | ||||||||||
| всего | в т. ч. | квартира | общая площадь, кв. м. | жилая площадь, кв. м. | число комнат | |||||||||||
| муж. пола | жен. пола | |||||||||||||||
| – – – – – – – – – – – – – – – – – – – – | – – – – – | да да да нет да нет да нет да да да нет да да да нет да да нет да да нет да да нет да да да да да нет да да да да да да да да да нет нет да да нет да да да да да нет да да да да да да нет да да да да да да да да нет да нет да да да да нет да да да да да да да да нет да да нет да да да да нет да да да да да да да да нет | да нет нет нет да нет да да нет нет нет нет да да да да нет нет нет нет нет нет да нет нет нет нет нет да нет нет да нет нет да нет нет нет нет нет да нет нет да нет нет нет нет да да нет да нет нет нет да да да нет нет да да нет нет да нет нет да нет нет да нет да нет нет нет да нет нет нет да да нет нет да да нет да нет да нет нет да да нет нет да нет нет да | да нет да нет нет нет нет да нет нет нет нет нет да нет да нет да нет да нет нет нет да нет нет да нет нет нет нет да нет нет нет нет да нет нет нет нет нет нет нет нет да нет нет нет нет нет нет да да нет нет нет нет нет нет нет да нет нет нет нет нет нет да нет да нет нет нет нет нет да нет нет нет нет да нет нет нет нет нет да нет да нет да нет да нет нет да нет да нет | да нет нет нет нет нет нет нет нет нет нет нет нет нет нет да нет нет нет нет нет нет нет да нет нет да нет нет нет нет да нет нет нет нет да нет нет нет нет нет нет нет нет да нет нет нет нет нет нет да да нет нет нет нет нет нет нет да нет нет нет нет нет нет да нет нет нет нет нет нет нет да нет нет нет нет да нет нет нет нет нет нет нет нет нет нет нет да нет нет да нет да нет | |||||||||||
18.1. По данным таблицы 1 постройте ряд распределения семей по числу членов. Постройте полигон распределения. Вычислите среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
18.2. По данным таблицы 1 постройте интервальный ряд распределения семей по обеспеченности общей площадью в расчёте на одного члена семьи. Постройте гистограмму распределения. Вычислите среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
18.3. По данным таблицы 1 постройте интервальный ряд распределения семей по обеспеченности жилой площадью в расчёте на одного члена семьи. Постройте гистограмму распределения. Вычислите среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
18.4. По данным таблицы 1 постройте ряд распределения квартир по числу комнат. Постройте полигон распределения. Вычислите среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
18.5. По данным таблицы 1 постройте интервальный ряд распределения семей по месячному доходу в расчёте на одного члена семьи. Постройте гистограмму распределения. Вычислите среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
18.6. На 80 сортоиспытательных участках определена урожайность пшеницы (ц/га):
| 23,9 | 22,4 | 23,1 | 16,3 | 21,8 | 21,6 | 20,5 | 20,4 | 20,6 | 21,3 | 25,1 | 21,7 | 21,3 | 20,2 | 21,0 | 20,7 |
| 18,2 | 20,2 | 25,1 | 19,6 | 24,0 | 22,5 | 23,2 | 16,4 | 21,9 | 21,7 | 20,6 | 20,5 | 20,7 | 21,2 | 25,0 | 24,3 |
| 21,6 | 21,2 | 20,9 | 20,6 | 18,1 | 19,5 | 20,1 | 25,0 | 21,6 | 20,5 | 20,4 | 20,6 | 21,3 | 25,1 | 21,7 | 22,8 |
| 21,3 | 20,2 | 22,9 | 23,4 | 22,1 | 17,3 | 20,8 | 22,6 | 19,5 | 21,4 | 19,6 | 22,3 | 24,1 | 22,7 | 20,3 | 21,2 |
| 20,0 | 21,7 | 17,2 | 21,2 | 24,1 | 20,6 | 23,0 | 23,5 | 22,2 | 17,4 | 20,9 | 22,7 | 19,6 | 21,5 | 19,5 | 21,7 |
Постройте интервальный ряд распределения участков по урожайности. Постройте гистограмму распределения. Вычислите среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
18.7. В результате взвешивания 90 коров получены следующие данные (ц):
| 4,5 | 4,7 | 3,4 | 5,4 | 4,6 | 5,0 | 3,8 | 4,7 | 5,6 | 4,0 | 5,1 | 4,9 | 3,3 | 3,5 | 4,3 |
| 5,5 | 4,5 | 4,2 | 5,1 | 4,9 | 4,5 | 3,2 | 4,0 | 5,9 | 4,7 | 5,8 | 4,4 | 4,6 | 4,8 | 5,7 |
| 3,3 | 5,5 | 4,5 | 5,1 | 3,7 | 4,8 | 5,3 | 4,1 | 4,2 | 5,2 | 4,8 | 3,4 | 3,4 | 4,5 | 4,7 |
| 4,6 | 5,7 | 4,5 | 4,5 | 4,7 | 4,5 | 4,6 | 3,7 | 5,1 | 4,6 | 4,9 | 4,1 | 4,7 | 5,2 | 4,2 |
| 5,0 | 4,8 | 3,6 | 3,8 | 4,3 | 5,2 | 4,6 | 4,4 | 5,1 | 5,0 | 4,4 | 3,6 | 4,0 | 5,3 | 4,7 |
| 5,5 | 4,4 | 4,6 | 4,8 | 5,4 | 3,9 | 4,4 | 4,9 | 3,7 | 5,2 | 4,5 | 5,1 | 4,0 | 4,8 | 5,3 |
Постройте интервальный ряд распределения коров по массе. Постройте гистограмму распределения. Вычислите среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
18.8. В случайном порядке отобрано 100 клубней картофеля и определен вес каждого клубня (г):
Постройте интервальный ряд распределения клубней по весу. Постройте гистограмму. Вычислите среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
18.9. В случайном порядке было отобрано 60 личных карточек студентов и выписаны их экзаменационные оценки по высшей математике:
<
Дата добавления: 2016-09-03; Мы поможем в написании ваших работ!; просмотров: 1523 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: |
Ген: 0.01 с.






