Контрольная работа по математике

1. Линейная алгебра

1.1. Действия с матрицами

1.1.1. Выполнить действия

 

2 * - 3 * ; *

 

 

1.2. Вычисление определителей

Найти значение, разложив по строке и методом Саррюса.

 

=

 

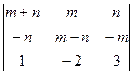
1.3. Обратная матрица

Найти обратную матрицу и проверить, что

 

А * А = Е

 

1.3.1. А = ; 1.3.2. А =

 

 

1.4. Системы линейных уравнений

Решить систему методом обратной матрицы, по формулам Крамера и методом Гаусса

 

 

 

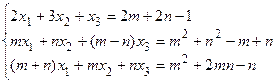
1. Аналитическая геометрия на плоскости

 

Дан с вершинами А (m + 1; n + 1), В (m; -n), С (-m; n). Найти

а) величину угла А; б) координаты точки пересечения медиан; в) координаты точки пересечения высот; г) длину высоты АН; д) площадь треугольника АВС; е) систему неравенств, задающих внутренность и сделать чертеж.

 

1. Дифференциальные исчисления

3.1. С помощью преобразований графиков построить графики функций:

3.1.1. y = 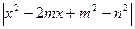(преобразовать график y = x )

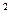3.1.2. y = (преобразовать график y = )

 

3.2. Найти пределы:

 

а) ()

б)

 

в)

 

г)

 

3.3. В точках x = 0 и x = n определить характер точек разрыва или установить непрерывность. Начертить график функции f(х).

 

f(x) =

 

3.4.Найти производные (x):

 

3.4.1. ; 3.4.2. y = ln ; 3.4.3. y = (nx) ; 3.4.4. - = mn.

 

3.5.Приложения производной

3.5.1. Составить уравнения касательных к графику функции y = , которые параллельны прямой 2mx + ny + mn = 0.

3.5.2. Построить график, проведя полное исследование функции f(x)

 

 

4. Интегральное исчисление

4.1.Найти неопределенные интегралы

 

а) ;

 

б) ;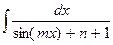

 

в) ;

 

 

г) ;

 

д)

 

4.2.Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:

и

 

5. Функции нескольких переменных

5.1.Найти , , , ,

А) ;

В)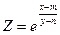

 

 

5.2.Показать, что функция удовлетворяет уравнению

.

 

 

6. Дифференциальные уравнения

6.1.Уравнения первого порядка

6.1.1. Найти общее решение уравнений

а) ;

б) ;

в) ;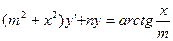

г)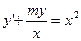

 

 

6.2.Уравнения высших порядков

6.2.1. Решить задачу Коши

а) ; ; ;

 

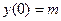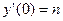б) ; ; ;

 

7. Теория вероятностей

7.1.Случайные события

7.1.1. В ящике (m+3) одинаковых пар перчаток черного цвета и (n+2) – белого цвета.

Найти вероятность того, что две наудачу извлеченные перчатки образуют пару.

7.1.2. В фирме работают 2(m+n) сотрудников, из них (m-1) женщин.

Найти вероятность того, что из 7 наугад отобранных сотрудников в эту группу попадут 5 мужчин.

 

7.2.Случайные величины

7.2.1. Закон распределения дискретной случайной величины имеет вид:

 

	-2	-1		m	m+n
	0.2	0.1	0.2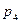

 

Найт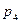и и , а так же дисперсию D(х), если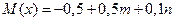

 

7.2.2. Плотность распределения непрерывной случайной величины имеет вид:

 

 

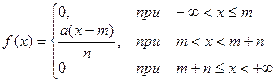
Найти:

а) параметра а;

б) функцию F(х);

в) ;

г) М(х) и D(x);

д) Построить графики F(х) и f(x).

 

8. Линейное программирование

8.1.Задача оптимального производства.

Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья: А, В, С. Потребность на каждую единицу j-го вида продукции i-го вида сырья, запас соответствующего вида сырья и прибыль от реализации единицы j-го вида продукции заданы в таблице:

 

Виды сырья	Виды продукции	Запасы сырья
I	II
А
В
С
Прибыль
План (ед)

 

Составить оптимальный план (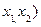, который обеспечивает максимальную прибыль . Решить задачу симплекс-методом и графически.

 

8.2.Транспортная задача

 

На трех складах , , хранится и единиц однородного груза. Этот груз доставляют потребителям , , , заказы которых составляют и 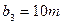соответственно.

 

 

потребности запасы
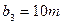
							m
			n
					m+1

 

 

Составить оптимальный план перевозок, учитывая, что задача является закрытой. Найти стоимость перевозок.