КОНТРОЛЬНАЯ РАБОТА №1
Общие требования к выполнению контрольной работы №1
Приступая к выполнению контрольной работы по математике необходимо изучить теоретический материал и выполнить соответствующие упражнения. Только после этого рекомендуется приступать к решению контрольной работы. Существенную помощь в решении контрольной работы может оказать пособие: Аглямова, З.Ш., Галимова, З.Х., Кожеманова, Т.Н. Математика: Методические указания к выполнению контрольной работы №1 – Казань: Изд-во «Познание» Института экономики, управления и права (г. Казань), 2009. – 67 с.
Студент выполняет вариант контрольной работы, соответствующий последней цифре номера его зачетной книжки (цифре 0 соответствует номер 10). Контрольная работа выполняется вручную в тетради, страницы которой имеют поля для замечаний преподавателя. Последовательность решения задач должна соответствовать последовательности заданий контрольной работы. Перед решением задачи необходимо переписать ее условие. Титульный лист выполняется на компьютере на листе формата А4 по размеру тетради и оформляется по примеру, приведенному в приложении (см.: Аглямова, З.Ш., Галимова, З.Х., Кожеманова, Т.Н. Математика: Методические указания к выполнению контрольной работы №1 – Казань: Изд-во «Познание» Института экономики, управления и права (г. Казань), 2009. – 67 с.)
Выполненная и оформленная контрольная работа должна быть представлена на кафедру высшей математики Набережночелнинского филиала Института экономики, управления и права (г. Казань) не позднее, чем за 30 дней до начала сессии.
ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ №1
1. Даны матрицы A, B, C. Вычислить матрицу D = AB + C.
| Номер варианта | А | В | С |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 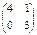
| |
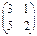
| 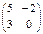
| 
| |
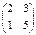
| 
| 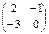
| |

| 
| 
| |

| 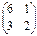
| 
|
2. Вычислить определители третьего порядка:
1)  , 2)
, 2) 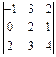 , 3)
, 3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  , 7)
, 7)  , 8)
, 8)  ,
,
9) 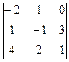 , 10)
, 10)  .
.
Решить систему линейных уравнений.
1)  , 2)
, 2)  ,
,
3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  ,
,
7)  , 8)
, 8)  ,
,
9)  ,10)
,10)  .
.
Задача межотраслевого баланса. Модель Леонтьева.
В таблице приведены данные об исполнении баланса за отчетный период в условных единицах. Вычислить матрицу прямых А затрат и проверить ее на по критерию продуктивности: матрица А продуктивна если a ij ≥ 0,  и существует номер j такой, что
и существует номер j такой, что  . Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление первой отрасли увеличивается вдвое, а второй на 20%.
. Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление первой отрасли увеличивается вдвое, а второй на 20%.
| Отрасль | Потребление | Конечный продукт | Валовый выпуск | ||
| Производство | 
| 
| 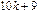
| 
| |

| 
| 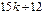
| 
|
 – номер варианта контрольной работы
– номер варианта контрольной работы
Составить общее уравнение прямой,
1) проходящей через точку  параллельно вектору
параллельно вектору 
2) проходящей через точку 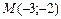 параллельно вектору
параллельно вектору 
3) проходящей через точки 
 и
и 
4) проходящей через точку  и составляющей с осью
и составляющей с осью  угол
угол  ;
;
5) проходящей через точку 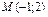 параллельно оси
параллельно оси  ;
;
6) проходящей через точку  параллельно оси
параллельно оси  ;
;
7) проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  ;
;
8) проходящей через точки 
 и
и 
9) проходящей через точку  и составляющей с осью
и составляющей с осью  угол
угол  ;
;
10) проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  .
.
6. Найти расстояние от прямой до точки  :
:
Координаты точки  вычисляются по формуле:
вычисляются по формуле:
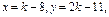
где 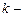 номер варианта контрольной работы.
номер варианта контрольной работы.
7. Построить график функции (при помощи преобразования графиков основных элементарных функций):
1) 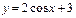 ; 6)
; 6)  ;
;
2) 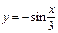 ; 7)
; 7) 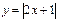 ;
;
3) 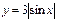 ; 8)
; 8)  ;
;
4)  ; 9)
; 9) 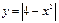 ;
;
5) 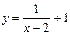 ; 10)
; 10) 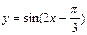 .
.
8. Значение функции 
 известно в точках
известно в точках 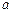 и
и  . С помощью линейной интерполяции найти значение в точке
. С помощью линейной интерполяции найти значение в точке  .
.
| Номер варианта | 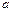
| 
| 
| 
| 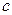
|
| -5 | -3 | -2 | |||
| -6 | -2 | -5 | |||
| -4 | |||||
| -4 | -1 | -2 | |||
| -2 | |||||
| -1 | |||||
| -5 | -2 |
9. Найти предел функции:
1)  ; 6)
; 6)  ;
;
2)  ; 7)
; 7)  ;
;
3)  ; 8)
; 8)  ;
;
4) 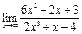 ; 9)
; 9)  ;
;
5) 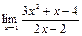 ; 10)
; 10) 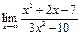 .
.
10. Найти предел функции:
1) 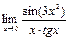 ; 2)
; 2) 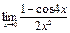 ;
;
3) 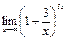 ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7) 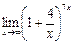 ; 8)
; 8)  ;
;
9)  ;
;  10)
10)  .
.
11. Вычислить производную функции:
1)  2)
2) 
3) 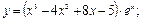 4)
4) 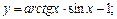
5)  , 6)
, 6)  ,
,
7)  8)
8) 
9)  10)
10)  .
.
12. Вычислить производную сложной функции:
1)  2)
2)  ;
;
3) 
 4)
4) 
5) 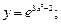 6)
6) 
7) 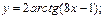 8)
8) 
9)  10)
10) 
13. Найти пределы, используя правило Лопиталя:
1) 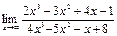 ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 
5)  6)
6)  ;
;
7) 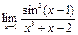 ; 8)
; 8) 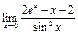 ;
;
9)  ; 10)
; 10) 






