Каждая контрольная работа содержит определенное количество примеров и задач. При выполнении их необходимо придерживаться следующих правил.
1. решение задач должно быть аккуратно выполнены в школьной тетради с оставленными полями для замечаний рецензента;
2. перед решением каждой задачи необходимо записать полный текст её условия;
3. чертежи к задачам выполняются в полном соответствии с исходными данными условий задачи и полученными при решении задач.
Работа защипывается, если она при проверке преподавателем получает положительную оценку (зачтено). Часто работа зачитывается но в ней имеются некоторые недочеты, указанные в рецензии. В этом случае необходимо исправления в конце той же тетради (после записи «Работа над ошибками»). Исправленная работа предъявляется на экзамене.
Если работа не зачтена, необходимо полностью или частично переделать её в той же тетради и с надписью «повторная» положить для проверки на кафедру.
Студенты, не получившие зачета по контрольной работе, к экзамену не допускаются. Зачтенные контрольные работы обязательно предъявляются на экзамене. Экзамен начинается с проверки студентов на умение решать задачи из контрольной работы. Если при этом обнаруживается несамостоятельность выполнения задач или непонимание смысла приведенных операций, то за экзамен студент получает оценку «неудовлетворительно» без последующего опроса.
ВЫБОР ВАРИАНТА осуществляется по последней цифре шифра в зачетной книжке студента: шифру 6589 соответствует вариант №9 (если оканчивается на «0», то вариант №10).
Список основной учебной литературы
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2.– М.: Высш. шк., 1997.
2. Письменный Д.Т. Конспект лекций по высшей математике: в 2 ч. Ч. 1 / Письменный Д.Т. – М.: Рольф, 2002. – 288 с.
Список дополнительной учебной литературы
3. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – Ростов н/Д: Феникс, 1997.
4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Ростов н/Д: Феникс, 1997.
5. Шипачев В.С. Высшая математика. – М.: Высш. шк., 1985.
6. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник – М.: ДИС, 1998.
7. Красс М.С. Математика для экономических специальностей: Учебник. – М.: ИНФРА, 1999.
8. Численное решение уравнений и обусловленность систем: Методич. указ. / Сост. Г.Л.Линдин; СМИ. Новокузнецк, 1986.
9. Бугров Я.С., Никольский С.М. Сборник задач по высшей математике. – Ростов н/Д: Феникс,1997.
10. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М. Наука, 1986.
Варианты контрольных работ
1-10. Найти наибольшее и наименьшее значения функции z = f(x, y) в замкнутой области D, заданной системой неравенств.
1. z = x2 + y2 – 9xy + 27; 3 ³ x ³ 0, 3 ³ y ³ 0.
2. z = x2 + 2y2 + 1; x ³ 0, 3 ³ x + y, y ³ 0.
3. z = 3 - 2x2 - y2 – xy; 1 ³ x, x ³ y, y ³ 0.
4. z = x2 + 3y2 + x - y; x ³ 1, y ³ -1, 1 ³ x + y.
5. z = x2 + 2y2 + 2xy; 1 ³ x ³ -1, 2 ³ y ³ 0.
6. z = 5x2 + y2 - 3xy + 4; x ³ -1, y ³ -1, 1 ³ x + y.
7. z = 10 + 2xy - x2; 4 - x2 ³ y ³ 0.
8. z = x2 - y2 + 2xy + 4x; 0 ³ x, 0 ³ y, x + y + 2 ³ 0.
9. z = x2 - 2 + xy; 0 ³ y ³ 4x2 – 4.
10. z = x2 + xy; 1 ³ x ³ -1, 3 ³ y ³ 0.
11-20. Найти интегралы
11.а). 
б). 
с). 
d). 
12. а). 
б).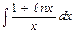 
с). 
d). 
13. а). 
б). 
с). 
d) 
14. а). 
б). 
с). 
d) 
105. а). 
б). 
с). 
d) 
16. а). 
б). 
с). 
d) 
17. а). 
б). 
с). 
d) 
18. а). (2x+3)e3xdx
б). 
с). 
d) 
19. а). e-3x(2-9x)dx
б). 
с). 
d) 
20. а). e-2x(4x-3)dx
б). 
с). 
d) 
Найти общее решение.
21. y’ +y cosx=e-sinx
22. x2 +x y’=y
23. y’+y ctgx=3 sinx cosx
24. x y’ +2y=x4
25. y’-y sinx=sinx cosx
26. y’ cosx +y =tgx
27. cosx dy + y sinx dx=dx
28. y’ +2xy=xe-x2
29. y’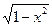 
+y=arcsinx
30. y’ 
= x lnx
31-32. Найти полный дифференциал функции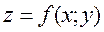 
31)  ;
32)  ;
33)  ;
34)  ;
35)  ;
| 36)  ;
37)  ;
38)  ;
39)  ;
40)  ;
|
41-50.
