Цель: научиться выбирать наилучшую регрессионную модель.
Основные формулы и понятия:
Модели нелинейной регрессии
Полиноминальная (степени p) 
Логарифмическая 
Гиперболическая 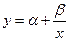
Дробно-линейная 
Показательная 
Степенная 
Логистическая 
Средняя ошибка аппроксимации 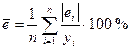 .
.
Электронная таблица Excel
В электронной таблице имеются возможности получения коэффициентов и значение детерминации для логарифмической, степенной, экспоненциальной функций и полинома произвольной степени. Для этого также, как и ранее, необходимо построить точечную диаграмму, а затем вызвать контекстное меню произвольной точки. В полученном меню необходимо выбрать пункт Добавить линию тренда, после него появится диалоговое окно (рис. 5), у которого на закладке Тип имеется возможность выбрать соответствующую нелинейную модель. Если кроме этого отметить опции Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации (R^2, то на графике кроме самой линии тренда появятся уравнение модели и значение коэффициента детерминации.
Например, для данных таблицы 5, построив линейную, экспоненциальную и логарифмическую модели, можно получить диаграмму, изображенную на рисунке 8:

Рисунок 8 Линия тренда
То есть имеем
линейную модель: y = –7,7145x + 240,14 R2 = 0,786,
экспоненциальную модель: y = 334,76e–0,0659x R2 = 0,789,
логарифмическую модель: y = –122,94Ln(x) + 457,51 R2 = 0,787.
Если имеется выбор между несколькими моделями, то самый простой способ — это задавать различные уровни тренда и выбрать ту модель, у которой значение коэффициента детерминации будет максимальным.
В данном случае значения коэффициентов детерминации несильно отличаются в различных моделях, поэтому нет объективных причин выбрать наилучшую, а следовательно, необходимо проводить дополнительные исследования либо используя среднюю ошибку аппроксимации, либо множественную регрессионную модель (которую мы будем рассматривать далее).
Хотя нами и получены модели, среди которых нельзя сразу выбрать лучшую, необходимо помнить о том, что прогноз, полученный на основании каждой модели, будет различным. Как было показано ранее (лабораторная работа № 2), прогноз, в случае использования линейной модели, при x = 17 будет равен 109,014. Прогноз, полученный на основании логарифмической модели, равен 109,1948, а на основании экспоненциальной модели — 109,1927. Эти значения получены подстановкой в уравнения моделей значения x = 17.
Использование результатов, полученных с помощью точечной диаграммы, имеет много недостатков. Во-первых, сам набор функций достаточно ограниченный, а одна из актуальных задач современной эконометрики заключается в подборе новых, более адекватных моделей, а во-вторых, проверять гипотезы о значимости коэффициентов, да и самой регрессии в целом придется вручную. К тому же посредством точечной диаграммы можно получить модель только для парного случая.
Поэтому иногда более удобно использовать преобразования, а уже затем надстройку Регрессия. Как мы уже знаем из теории, любая из предложенных нелинейных моделей может быть сведена к линейной либо заменой переменных, либо логарифмированием. Поэтому в таблицу исходных данных добавляют дополнительные столбцы, в которых находятся значения логарифмов, а затем строят регрессионную модель между необходимыми столбцами. Однако в этом случае нужно помнить о том, что, переходя к линейной модели, посредством логарифмирования получают изменённые значения параметров, которые затем необходимо восстанавливать.
Из экономической теории известно, что спрос является убывающей функцией цены, то есть при увеличении цены спрос убывает. Следовательно, разумной будет попытка найти лучшую модель среди убывающих функций. Имеется огромное количество функций, которые при некоторых значениях параметров являются убывающими, например, линейная, гиперболическая, показательная, с основанием меньше 1, и т. д. Рассмотрим способ построения показательной модели  . После логарифмирования данная модель примет вид
. После логарифмирования данная модель примет вид  . Следовательно, для получения параметров модели необходимо значения x задавать как и прежде, а значения y заменить на значения логарифмов, то есть задать Входной интервал Y в виде D1:D16. В этом случае исходная таблица данных, в которой имеется дополнительный столбец, будет иметь вид (табл. 10):
. Следовательно, для получения параметров модели необходимо значения x задавать как и прежде, а значения y заменить на значения логарифмов, то есть задать Входной интервал Y в виде D1:D16. В этом случае исходная таблица данных, в которой имеется дополнительный столбец, будет иметь вид (табл. 10):
Таблица 10 Таблица исходных данных
| Номер наблюдения | Цена x (т.) | Спрос y (тыс. шт.) | ln(y) |
| 15,09т. | 125,1779 | 4,829736 | |
| 15,21т. | 123,8094 | 4,818744 | |
| 15,28т. | 121,175 | 4,797236 | |
| 15,49т. | 116,9143 | 4,761441 | |
| 15,54т. | 119,8643 | 4,78636 | |
| 15,62т. | 118,0681 | 4,771261 | |
| 15,70т. | 123,5887 | 4,816959 | |
| 15,91т. | 117,0877 | 4,762923 | |
| 15,92т. | 116,1699 | 4,755054 | |
| 15,95т. | 118,3436 | 4,773592 | |
| 16,31т. | 116,2008 | 4,75532 | |
| 16,33т. | 111,4565 | 4,713635 | |
| 16,60т. | 115,1026 | 4,745824 | |
| 16,69т. | 110,1056 | 4,70144 | |
| 16,76т. | 110,0231 | 4,700691 |
После вызова надстройки Регрессия будет получена итоговая таблица (табл. 11).
Таблица 11 Итоговая таблица
| ВЫВОД ИТОГОВ | |||||||||
| Регрессионная статистика | |||||||||
| Множественный R | 0,888266 | ||||||||
| R-квадрат | 0,789016 | ||||||||
| Нормированный R-квадрат | 0,772787 | ||||||||
| Стандартная ошибка | 0,019221 | ||||||||
| Наблюдения | |||||||||
| Дисперсионный анализ | |||||||||
| Df | SS | MS | F | Значимость F | |||||
| Регрессия | 0,01796 | 0,01796 | 48,61611 | 9,73E–06 | |||||
| Остаток | 0,004803 | 0,000369 | |||||||
| Итого | 0,022763 | ||||||||
| Коэффи- циенты | Стандартная ошибка | t- статистика | P- значение | Нижние 95 % | Верхние 95 % | ||||
| Y-пересечение | 5,813415 | 0,1503 | 38,67869 | 8,27E–15 | 5,488711 | 6,138119 | |||
| Цена x (т.) | –0,06591 | 0,009452 | –6,97253 | 9,73E–06 | –0,08633 | –0,04549 | |||
Используя раздел Коэффициенты можно записать итоговую модель вид  .
.
После потенцирования будет  . Аналогичным образом можно построить произвольную регрессионную модель.
. Аналогичным образом можно построить произвольную регрессионную модель.
При подборе оптимальной модели кроме коэффициента детерминации можно использовать и среднюю ошибку аппроксимации. Данные вычисления достаточно очевидны, и их рекомендуется выполнить самостоятельно на основании полученных после вызова надстройки данных.






