Изучение дифракции Фраунгофера от одной щели

ЦЕЛЬ РАБОТЫ:

* Знакомство со схемой дифракции Фраунгофера от одной щели в когерентном свете.

* Определение углов дифракции в параллельных лучах.

 

 

Углы дифракции, соответствующие дифракционным максимумам:

 

sin j ₁» ; sin » ; sinj₃ или:

первого порядка d sin j₁ = ± 1,43l;

второго порядка d sin j₂ = ± 2,46l;

третьего порядка d sin j₃ = ± 3,47l;

четвёртого порядка d sin j₄ = ± 4,5l.

 

 

ТАБЛИЦА 1 Результаты измерений при l = 400нм

d, мм	2,0	2,5	3,0	3,5	4,0
а 1, мм	2,65	2,12	1,59	1,32	1,06
а 2, мм	4,77	3,18	3,18	2,65	2,12
а 3, мм	6,89	5,3	4,24	3,71	3,18
а 4, мм	8,48	6,89	5,83	4,77	4,24
sin j 1´10ˉ3	0,265	0,212	0,159	0,132	0,106
sin j 2´10ˉ3	0,477	0,318	0,318	0,265	0,212
sin j 3´10ˉ3	0,689	0,53	0,424	0,371	0,318
sin j 4´10ˉ3	0,848	0,689	0,583	0,477	0,424

 

sin j₁ = 1,43l/d= 1.43х4х10ˉ⁷/2х10ˉ³=2,86х10ˉ⁴

sin j₂ = 2,46l/d=2,46 х4х10ˉ⁷/2х10ˉ³=4,92х10ˉ⁴

sin j₃ = 3,47l/d= 3,47х4х10ˉ⁷/2х10ˉ³=6,94х10ˉ⁴

sin j₄ = 4,5l/d= 4,5х4х10ˉ⁷/2х10ˉ³=9х10ˉ⁴

ТАБЛИЦА 2 Результаты измерений при l = 500нм

d, мм	2,0	2,5	3,0	3,5	4,0
а 1, мм	3,44	2,65	2,12		1,59
а 2, мм	6,09	4,77	3,71	3,44	2,91
а 3, мм	8,21	7,68	5,83	4,77	4,24
а 4, мм	-	9,01	7,42	6,09	5,3
sin j 1´10ˉ3	0,344	0,265	0,212	0,2	0,159
sin j 2´10ˉ3	0,609	0,477	0,371	0,344	0,291
sin j 3´10ˉ3	0,821	0,768	0,583	0,477	0,424
sin j 4´10ˉ3	-	0,901	0,742	0,609	0,53

sin j₁ = 1,43l/d= 1.43х5х10ˉ⁷/2х10ˉ³=3,57х10ˉ⁴

sin j₂ = 2,46l/d=2,46 х5х10ˉ⁷/2х10ˉ³=6,15х10ˉ⁴

sin j₃ = 3,47l/d= 3,47х5х10ˉ⁷/2х10ˉ³=8,67х10ˉ⁴

sin j₄ = 4,5l/d= 4,5х5х10ˉ⁷/2х10ˉ³=11,25х10ˉ⁴

ТАБЛИЦА 3 Результаты измерений при l = 580нм

d, мм	2,0	2,5	3,0	3,5	4,0
а 1, мм		3,18	2,65		1,85
а 2, мм	6,89	5,83	4,77	4,24	3,41
а 3, мм	-	7,95	6,89	5,83	4,77
а 4, мм	-	-	8,48	7,42	6,36
sin j 1´10ˉ3	0,4	0,318	0,265	0,2	0,185
sin j 2´10ˉ3	0,689	0,583	0,477	0,424	0,341
sin j 3´10ˉ3	-	0,793	0,689	0,583	0,477
sin j 4´10ˉ3	-	-	0,848	0,742	0,636

sin j₁ = 1,43l/d= 1.43х5,8х10ˉ⁷/3х10ˉ³=2,76х10ˉ⁴

sin j₂ = 2,46l/d=2,46 х5,8х10ˉ⁷/3х10ˉ³=4,76х10ˉ⁴

sin j₃ = 3,47l/d= 3,47х5,8х10ˉ⁷/3х10ˉ³=6,71х10ˉ⁴

sin j₄ = 4,5l/d= 4,5х5,8х10ˉ⁷/3х10ˉ³=8,7х10ˉ⁴

ТАБЛИЦА 4 Результаты измерений при l = 630нм

d, мм	2,0	2,5	3,0	3,5	4,0
а 1, мм	4,24	3,18	2,65	2,38
а 2, мм	7,95	6,36	5,3	4,24
а 3, мм	-	9,01	7,42	6,36	5,03
а 4, мм	-	-	9,01	7,95	6,89
sin j 1´10ˉ3	0,424	0,318	0,265	0,238	0,2
sin j 2´10ˉ3	0,795	0,636	0,53	0,424	0,4
sin j 3´10ˉ3	-	0,901	0,742	0,636	0,503
sin j 4´10ˉ3	-	-	0,901	0,795	0,689

sin j₁ = 1,43l/d= 1.43х6,3х10ˉ⁷/3х10ˉ³=3х10ˉ⁴

sin j₂ = 2,46l/d=2,46 х6,3х10ˉ⁷/3х10ˉ³=5,17х10ˉ⁴

sin j₃ = 3,47l/d= 3,47х6,3х10ˉ⁷/3х10ˉ³=7,29х10ˉ⁴

sin j₄ = 4,5l/d= 4,5х6,3х10ˉ⁷/3х10ˉ³=9,45х10ˉ⁴

Вывод: При неизменной длине волны с увеличением ширины щели уменьшается ширина полос максимумов, следовательно, уменьшается величина sin j. Погрешности в определении sin j объясняются неточностью снятия размеров с экрана монитора.

 

ЛАБОРАТОРНАЯ РАБОТА № 4.3

 

ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ

С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА

ЦЕЛЬ РАБОТЫ:

* Знакомство с моделированием явления интерференции света в тонких плёнках.

* Изучение интерференции полос равной толщины в схеме колец Ньютона.

* Определение радиуса кривизны линзы.

 

 

Значения радиусов тёмных колец Ньютона:

 

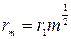
Формула для определения радиуса кривизны линзы:

 

 

Таблица: Результаты измерений и расчетов.

l1= 4x10ˉ7(m) R 1 = 0.5(m)	l2 = 6,4x10ˉ7(m) R 2 = 1.80(m)
r3 x10ˉ3	r5 x10ˉ3	r4 x10ˉ3	r6 x10ˉ3	r3 x10ˉ3	r5 x10ˉ3	r4 x10ˉ3	r6 x10ˉ3
0,783	1,0125	0,9	1,1025	1.86	2.41	2.14	2.62
=0,51(m)	=0,51(m)	=2,0 (m)	=2,856 (m)

r₃ = 0,45х3^1/2 x10ˉ³»0,45х1,74 x10ˉ³= 0,783x10ˉ³ (m)

r₅ = 0,45х5^1/2 x10ˉ³»0,45x2,25 x10ˉ³= 1,0125x10ˉ³ (m)

r₄ = 0,45х4^1/2 x10ˉ³»0,45x2 x10ˉ³= 0,9x10ˉ³ (m)

r₆ = 0,45х6^1/2 x10ˉ³»0,45x2,45 x10ˉ³= 1,1025x10ˉ³ (m)

R 1=(1,0215-0,6130)x10ˉ⁶/(5-3)x4x10ˉ⁷= 0,4085x10ˉ⁶/8x10ˉ⁷=0,51(m)

R 2=(1,2155-0,81)x10ˉ⁶/(6-4)x4x10ˉ⁷= 0,4055x10ˉ⁶/8x10ˉ⁷=0,51(m)

 

r₃ = 1.07х3^1/2 x10ˉ³»1.07х1,74 x10ˉ³= 1,86x10ˉ³(m)

r₅ = 1.07х5^1/2 x10ˉ³»1.07x2,25 x10ˉ³=2,41x10ˉ³(m)

r₄ = 1.07х4^1/2 x10ˉ³»1.07x2 x10ˉ³= 2,14x10ˉ³(m)

r₆ = 1.07х6^1/2 x10ˉ³»1.07x2,45 x10ˉ³=2,62x10ˉ³(m)

R 1=(5,8081-3,4596)x10ˉ⁶/(5-3)x4x10ˉ⁷=1,62121x10ˉ⁶/8x10ˉ⁷=2,0 (m)

R 2=(6,8644-4,5796)x10ˉ⁶/(6-4)x4x10ˉ⁷= 2,2848x10ˉ⁶/8x10ˉ⁷=2,856 (m)

 

Вывод: Установленный радиус кривизны и полученный при расчетах примерно одинаковы. Погрешности в определении радиуса кривизны объясняются неточностью вычисления квадратных корней порядка колец и растут с увеличением длины волны света.

 

 

ЛАБОРАТОРНАЯ РАБОТА № 4.4

ДИФРАКЦИЯ И ИНТЕРФЕРЕНЦИЯ

 

ЦЕЛЬ РАБОТЫ:

* Знакомство с моделированием процесса сложения когерентных электромагнитных волн.

* Экспериментальное исследование закономерностей взаимодействия световых волн от двух источников (щелей).

 

 

 

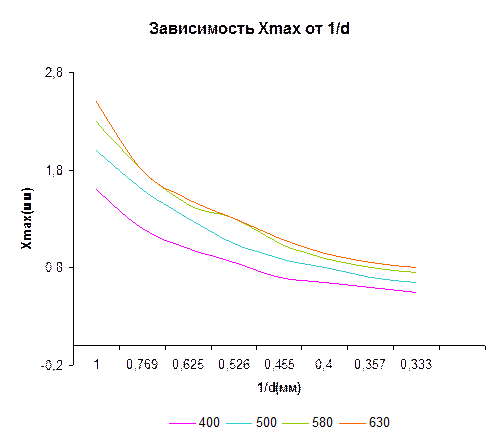
ТАБЛИЦА 1. Результаты измерений при l = 400 нм

d[мм]	1,0	1,3	1,6	1,9	2,2	2,5	2,8	3,0
XMAX[мм]	1,6	1,2	1,0	0,85	0,7	0,65	0,6	0,55
1/XMAX [мм-1]	0,625	0,833		1,176	1,429	1,538	1,667	1,818

ТАБЛИЦА 2. Результаты измерений при l = 500нм

d[мм]	1,0	1,3	1,6	1,9	2,2	2,5	2,8	3,0
XMAX[мм]	2,0	1,6	1,3	1,05	0,9	0,8	0,7	0,65
1/XMAX [мм-1]	0,5	0,625	0,769	0,952	1,111	1,25	1,429	1,538

ТАБЛИЦА 3. Результаты измерений при l = 580нм

d[мм]	1,0	1,3	1,6	1,9	2,2	2,5	2,8	3,0
XMAX[мм]	2,3	1,8	1,45	1,3	1,05	0,9	0,8	0,75
1/XMAX [мм-1]	0,435	0,555	0,69	0,769	0,952	1,111	1,25	1,333

ТАБЛИЦА 4. Результаты измерений при l = 630нм

d[мм]	1,0	1,3	1,6	1,9	2,2	2,5	2,8	3,0
XMAX[мм]	2,5	1,8	1,5	1,3	1,1	0,95	0,85	0,8
1/XMAX [мм-1]	0,435	0,555	0,69	0,769	0,952	1,111	1,25	1,333

 

 

λ1L=(1.6-0.55)/(1-0.333)=1.574

λ2L=(2.0-0.65)/(1-0.333)=2.024

λ3L=(2.3-0.75)/(1-0.333)=2.324

λ1L=(1.6-0.55)/(1-0.333)=2.549

Вывод: При увеличении расстояния между щелями (при постоянной длине волны) расстояние между максимумами уменьшается, а при увеличении длины волны увеличивается.