Лабораторная работа №36,4. Эвольвентные зубчатые зацепления
Основные положения
ЗУБЧАТЫЕ МЕХАНИЗМЫ находят самое широкое применение в машинах. Они используются для изменения угловой скорости ведомого звена. При этом совершенно необходимым является требование постоянства передаточного отношения не только за целые обороты зубчатых колес, но и в течение зацепления каждой пары зубьев. Условие, которому должны удовлетворять профили зубьев для сохранения постоянного передаточного отношения, определяется теоремой зацепления, гласящей о том, что общая нормаль АВ к профилям зубчатых колес П1 и П2 в точке касания К делит МЕЖЦЕНТРОВОЕ РАССТОЯНИЕ О1 О2 НА ЧАСТИ, ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ УГЛОВЫМ СКОРОСТЯМ. Точка пересечения нормали и межцентрового расстояния называется ПОЛЮСОМ ЗАЦЕПЛЕНИЯ (Р) (Рис.I). Итак, передаточное отношение
,
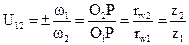где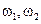 
- угловые скорости колес
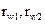- начальные окружности колес
z1,z2 - число зубьев колес.
Для того чтобы передаточное отношение было постоянным, необходимо выбрать такой профиль зубьев, для которого при зацеплении пары зубьев в любом положении полюс зацепления Р сохранял свое положение на линии центров. Этому условию удовлетворяют профили зубьев, очерченные эвольвентами окружностей.
ЭВОЛЬВЕНТНОЙ называется кривая МОМ1, описываемая точкой М прямой NN, которая катится без скольжения по окружности радиуса rB=OA (Рис.2). Из построения видно, что эвольвента будет располагаться вне окружности радиуса rB и начинается на этой окружности. Окружность, по которой катится прямая, называется ОСНОВНОЙ ОКРУЖНОСТЬЮ.
Уравнение эвольвенты в параметрической форме (параметр угол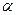 
, рис.2) имеет вид 
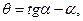
радиус вектор эвольвенты находится из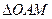 
,
где 
- эвольвентная функция
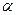- угол давления на уровне радиуса
Тригонометрическую функцию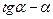 
называют инволютой угла 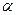т.е.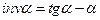 
На рис.8 показано зацепление двух зубьев. Нормаль к профилям зубьев в общей точке М их контакта проходит через полюс Р и по свойству эвольвенты касается основных окружностей колес. При вращении колес точка контакта М перемещается по этой внутренней касательной, которая является линией зацепления. Давление от колеса к колесу передается по линии зацепления под углом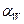 
к линии 
являющейся общей касательной к начальным окружностям колес. Угол 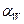называется УГЛОМ ЗАЦЕПЛЕНИЯ.
На рис. 4 изображена часть зубчатого колеса. Боковые поверхности зубьев очерчены по эвольвенте. Расстояние между односторонними профилями двух смежных зубьев колеса, взятое по дуге, называется ШАГОМ ЗАЦЕПЛЕНИЯ.
ДЕЛИТЕЛЬНОЙ ОКРУЖНОСТЬЮ называется такая окружность, по которой шаг равен стандартному шагу. Число зубьев колеса – z должно быть целым, поэтому шаг зацепления должен быть кратен длине окружности, по которой он откладывается. Следовательно, если обозначить через радиус r - радиус делительной окружности колеса, Р – окружной шаг по этой окружности и z – число зубьев колеса, то должны иметь место равенства.
,
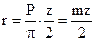
Величина m – отношение окружного шага к числу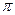 
называемое модулем зубьев. Модуль измеряется в миллиметрах и служит основным параметром, определяющим размеры зубчатого колеса и его элементов. Значение модуля определяется стандартом.
Зубчатое колесо называется НУЛЕВЫМ, если по делительной окружности толщина зуба S равна ширине впадины SВ. размеры ЭЛЕМЕНТОВ НУЛЕВЫХ КОЛЕС, выраженных через модуль, приведены в таблице.
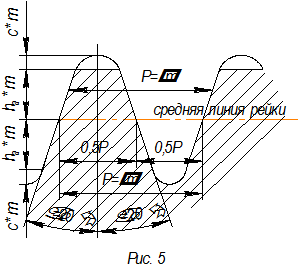
| Элементы колеса и зацепления | Обозначение | Нулевое колесо |
| Шаг зацепления | P |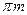 
|
| Радиус делительной окружности | r | 0,5mz |
| Высота головки зуба | ha | m |
| Высота ножки зуба | h1 | 1,25m |
| Радиус окружности выступов | ra | r + m |
| Радиус окружности впадин | r1 | r – 1,25m |
| Толщина зуба по делительной окружности | S |
|
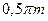
| Угол зацепления |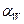
| 200 |
| Радиус основной окружности | rB |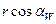 
|
| Межцентровое расстояние | aw | 0,5m(z1+z2) |
При нарезании зубчатых колес методом обкатки инструмент изготовляется либо в виде колеса с эвольвентными профилями зубьев (так называемый долбяк), либо – зубчатой рейки с прямолинейными профилями зубьев (так называемая гребенка). В процессе нарезания зубчатого колеса заготовке и инструменту сообщается такое относительное движение, какое они имели бы, находясь в зацеплении.
Инструмент имеет дополнительное возвратно-поступательное движение вдоль оси колеса, во время осуществления которого режущая кромка инструмента вырезает на заготовке профиль зуба.
Из рис.5 видно, что шаг рейки имеет одинаковую величину по любой прямой (0-0 или I-I), параллельной основанию рейки. Можно провести такую линию 0-0, по которой толщина зуба равна ширине впадины. Эта линия называется модульной прямой рейки.
Для того, чтобы нарезать нулевое колесо, необходимо установить гребенку так, чтобы модульная прямая ее была удалена от центра заготовки на расстояние радиуса делительной окружности r, т.е. чтобы делительная окружность заготовки обкатывалась без скольжения по модульной прямой. Тогда на нарезаемом колесе получатся зубья, толщина которых по делительной окружности будет равна ширине впадины.
Пусть мы отодвинули рейку от центра заготовки колеса на величину xm. Тогда при нарезании зубьев делительная окружность будет катится без скольжения по линии I-I, которую назовем начальной прямой. Из рисунка видно, что в этом случае толщина зуба гребенки на начальной прямой будет меньше впадины, значит, на нарезаемом колесе по делительной окружности толщина зуба будет больше, чем ширина впадины (так как при обкатке зуб рейки образует на заготовке впадину). Зубчатые колеса, нарезанные методом обкатки с удалением гребенки от центра заготовки, по сравнению с нулевой установкой, при которой делительная окружность касается модульной прямой, называются ПОЛОЖИТЕЛЬНЫМИ КОЛЕСАМИ, а дополнительное удаление гребенки – ПОЛОЖИТЕЛЬНЫМ СМЕЩЕНИЕМ (СДВИГОМ).(Рис.6).
Можно дать гребенке отрицательное смещение (сдвиг), т.е. приблизить ее к центру заготовки по сравнению с нулевой установкой. Тогда на заготовке будет нарезано целое число зубьев с очертанием бокового профиля их по эвольвенте. Однако в этом случае по делительной окружности толщина зуба будет меньше ширины впадины. Такое колесо называется ОТРИЦАТЕЛЬНЫМ. Отношение смещения к модулю называется КОЭФФИЦИЕНТОМ СМЕЩЕНИЕМ (ОТНОСИТЕЛЬНЫМ СДВИГОМ) и обозначается через x.
Изготовление положительных, так называемых корригированных, колес производится с целью увеличения прочности зубьев (устранения подреза профиля малого колеса), уменьшения наибольших значений удельного скольжения.
Корригированные колеса могут быть введены в сцепления между собой и с нулевыми колесами. Формулы для расчета элементов корригированных колес и их зацепления приведены в таб.1.
Вычерчивание зубьев эвольвентного профиля нулевого (нормального) и коррегированных колес методом обкатки
Цель работы
Ознакомление с нарезанием нулевых и корригированных зубчатых колес с эвольвентным профилем.
Объем работы.
Нарезать на заготовке по 3 зуба нулевого и положительного колес, 1 зуб с отрицательной коррекцией.
