Проиллюстрируем теперь применение операций над множествами для решения задач о нахождении числа элементов, заданных несколькими условиями. Ниже будем рассматривать только конечные множества А и через 
обозначать число их элементов.
При решении задач будем пользоваться формулой включений и исключений для двух конечных множеств А и В:
,
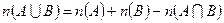и формулой включений и исключений для трех конечных множеств А, В и С:
.
Задача.
На вступительном экзамене по математике были предложены три задачи: по алгебре, планиметрии и стереометрии. Из 1000 абитуриентов задачу по алгебре решили 800, по планиметрии – 700, по стереометрии – 600 абитуриентов. При этом задачи по алгебре и планиметрии решили 600 абитуриентов, по алгебре и стереометрии – 500, по планиметрии и стереометрии – 400. Все три задачи решили 300 абитуриентов. Существуют ли абитуриенты, не решившие ни одной задачи, и если да, то сколько их?
Решение. Пусть
1) U – множество всех абитуриентов,
2) А – множество абитуриентов, решивших задачу по алгебре,
3) В – множество абитуриентов, решивших задачу по планиметрии,
4) С – множество абитуриентов, решивших задачу по стереометрии.
По условию задачи составим таблицу числа элементов множеств (таблица 1).
Таблица 1.
| Множества | Обозначение числа элементов множества | Число элементов множества |
| Множество всех абитуриентов. | 
| |
| Множество абитуриентов, решивших задачу по алгебре. |
| |
| Множество абитуриентов, решивших задачу по планиметрии. | 
| |
| Множество абитуриентов, решивших задачу по стереометрии. | 
| |
| Множество абитуриентов, решивших задачу по алгебре и планиметрии. |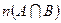 
| |
| Множество абитуриентов, решивших задачу по алгебре и стереометрии. | 
| |
| Множество абитуриентов, решивших задачу по планиметрии и стереометрии. | 
| |
| Множество абитуриентов, решивших задачу по алгебре, планиметрии и стереометрии. | 
|
В множество 
включены все абитуриенты, решившие хотя бы одну задачу. По формуле включений и исключений для трех конечных множеств имеем 
. Отсюда следует, что не все поступившие решили хотя бы одну задачу. Ни одной задачи не решили 
(абитуриентов).
Рис.5.
На рисунке 5 это решение проиллюстрировано с помощью диаграмм Эйлера – Венна.
Вернуться к конспектам уроков
Оглавление
1. Множества и их элементы.. 1
2. Характеристическое свойство множества. 2
3. Подмножества. 3
4. Операции над множествами. 4
4.1. Пересечение множеств. 4
4.2. Объединение множеств. 4
4.3. Разность множеств. 5
5. Формулы включений и исключений. 6
