Характеристическое свойство множества

Элементы теории множеств

(Методическое пособие для учащихся

Х классов физико-математического профиля)

Автор: Хомутова Л.Ю.

Москва

Год

«Множество есть многое,
мыслимое нами как единое».

Г. Кантор

Множества и их элементы

В повседневной жизни постоянно различные совокупности предметов называют одним словом. Совокупность документов называют архивом, собрание музыкантов – оркестром, группу лошадей – табуном, собрание книг – библиотекой и т. д.

Математическим понятием, отражающим объединение некоторых объектов, предметов или понятий в единую совокупность, является понятие множества. Это понятие в математике является первичным, не определяемым, таким же, как понятие точки и прямой в геометрии, – к более простым понятиям оно не сводится.

Приведем примеры множеств:

· Множество всех людей, живущих в настоящее время на Земле.

· Множество всех рыб в Тихом океане.

· Множество звезд в Галактике.

· Множество всех натуральных чисел.

· Множество всех действительных чисел , удовлетворяющих условию .

· Множество учащихся данной школы.

Предметы, объекты, образующие данное множество, называются его элементами. Например, Александр I является элементом множества российских императоров, а число 9 – элементом множества натуральных чисел, а число не является элементом множества целых чисел.

Обычно множества обозначаются латинскими прописными буквами A, B, C, D,X,Y,W и т. д., а их элементы – строчными буквами a, b, c, d, x, y, w и т. д. То обстоятельство, что объект a является элементом множества А, записывают так: . Если объект а не является элементом множества А, то пишут: .

Множества А и В называются равными, если они содержат одни и те же элементы. Например, равны множества и 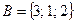. Равенство множеств А и В записывают в виде А=В.

Характеристическое свойство множества

Различают множества конечные и бесконечные. Конечным называется множество, состоящее из конечного числа элементов. Среди конечных множеств выделяют пустое множество, не имеющего ни одного элемента. Его называют пустым множеством и обозначают символом . Примерами пустых множеств являются множество людей выше трех метров роста, множество нечетных чисел, делящихся на два, и т. д. Множество, не являющееся конечным, называется бесконечным множеством.

Имеется два существенно различных способа задания множества. Первый способ состоит в том, что множество задается указанием всех его элементов. В этом случае говорят, что множество задано перечислением всех своих элементов, или списком элементов.

Перечислением элементов можно задать лишь конечные множества. И даже для них это не всегда легко сделать: трудно перечислить все элементы конечного множества, состоящего из всех людей, живущих на Земле.

Второй способ задания множества применим как к конечным, так и к бесконечным множествам. Он состоит в том, указывается свойство, которым обладают все элементы рассматриваемого множества и не обладают никакие другие объекты. Такое свойство называется характеристическим свойством множества. Если множество А задано характеристическим свойством Р, то пишут:

Эту запись читают так: множество А состоит из тех и только тех элементов, которые обладают свойством Р.

означает, что множество В состоит из всех нечетных натуральных чисел.

Подмножества

Множество В является подмножеством множества А, если каждый элемент х из множества В является вместе с тем и элементом множества А. В этом случае пишут: . Здесь знак является знаком включения одного множества в другое.

Рассмотрим множества:

1) В – множество всех четырехугольников,

2) С – множество всех параллелограммов,

3) D – множество всех прямоугольников,

4) Е – множество всех квадратов.

В смысле множества фигура каждого следующего типа является частным случаем фигуры предыдущего типа (параллелограмм – частный случай четырехугольника, прямоугольник – параллелограмма, квадрат – прямоугольника). Это означает, что каждое следующее множество является подмножеством предыдущего. Поэтому

Для иллюстрации соотношения между множествами пользуются схемами, называемыми диаграммами Эйлера – Венна, на которых множества изображаются овалами, в частности кругами.

Леонард Эйлер (1707 – 1783) – один из величайших математиков {VIII в., швейцарец; Дж. Венн (1834 – 1923) – английский математик.

На рисунке 1 с помощью кругов показано соотношение между множествами B, С, D, Е.

Рис. 1

Операции над множествами

Пересечение множеств

Если даны два множества, то можно образовать новое множество, составленное из общих элементов этих множеств. Например, общей частью множеств будет множество , которое называют пересечением множеств А и В.

Определение. Пересечением множеств А и В называется новое множество, содержащее те и только те элементы, которые входят одновременно и в множество А, и в множество В.

Пересечение множеств А и В обозначают :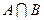

Например, если А – множество всех прямоугольников, В – множество всех ромбов, то 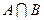– множество всех квадратов.

Геометрическую иллюстрацию операции пересечения множеств А и В дают диаграммы Эйлера – Венна (рис. 2).

а) б)

Рис. 2

На рисунке 2,а заштриховано множество 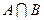, на рисунке 2,б множества А и В не пересекаются, т. е. .

Операция пересечения множеств применяется там, где требуется найти элементы, удовлетворяющие сразу двум условиям. Например, множество натуральных чисел, кратных 15, – это пересечение множества натуральных чисел, кратных 3, и множества натуральных чисел, кратных 5, т. е.

Объединение множеств

Из двух множеств А и В можно образовать новое множество, объединяя все элементы множества А и все элементы множества В. Например, объединяя элементы множества с элементами множества , получим новое множество 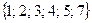, которое называют объединением множеств А и В. При этом общие элементы 3 и 5 входят в объединение один раз.

Определение. Объединением множеств А и В называется новое множество, состоящее из тех и только тех элементов, которые входят хотя бы в одно из множеств А или в множество В.

Объединение множеств А и В обозначают :

а) б)

Рис. 3.

Диаграммы Эйлера – Венна, соответствующие операции объединения множеств А и В, построены на рисунке 3. На них заштрихованы множества .

Разность множеств

Определение. Разностью двух множеств А и В называют такое множество, в которое входят элементы из множества А, не принадлежащие множеству В.

Разность множеств А и В обозначают А/В. Диаграммы Эйлера – Венна, соответствующие операции вычитания множеств А и В, построены на рисунке 4. На нем заштрихованы множества А/В. Если А=В, то А/В= .

а) б) в)

Рис. 4.

В случае, когда В есть подмножество множества А, разность А/В называют дополнением множества В в множестве А и обозначают . Например, дополнением множества четных чисел в множестве всех целых чисел является множество нечетных чисел.