Статистический критерий — строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза с известным уровнем значимости. Построение критерия представляет собой выбор подходящей функции от результатов наблюдений (ряда эмпирически полученных значений признака), которая служит для выявления меры расхождения между эмпирическими значениями и гипотетическими.
Для каждого вида проверяемых гипотез разработаны специальные критерии, среди которых чаще всего используют - критерий нормального распределения и распределения Стьюдента, -критерий Фишера, распределения Пирсона («хи-квадрат») и другие.
Для построения статистического критерия, позволяющего проверить некоторую гипотезу, необходимо следующее:
Сформулировать проверяемую гипотезу. Наряду с проверяемой гипотезой формулируется также конкурирующая гипотеза (альтернативная);
выбрать уровень значимости, контролирующий допустимую вероятность ошибки первого рода;
определить область допустимых значений и так называемую критическую область;
принять то или иное решение на основе сравнения фактического и критического значений критерия.
Критерий Фишера в парной регрессии
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам. Для применения критерия Фишера мы должны располагать исходными данными не менее 8 значений фактора (признака).
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
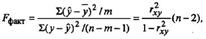
где n - число наблюдений;
m - число параметров при факторе х.
F табличный - это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а - вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Табличное значение критерия Фишера вычисляют следующим образом:
Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
Определяют k2, которое определяется по формуле n - m - 1, где n - число наблюдений, m - количество факторов. Например, в однофакторной модели k2 = n - 2.
На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n - m - 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критериий Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента. Для применения критерия Стьюдента мы должны располагать исходными данными не менее 2-3 значений фактора (признака).
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:

Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так

Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт.
Статистические критерии должны подтверждать друг друга, а не противоечить.
Теорема Гаусса-Маркова.
Доказано, что для получения по МНК наилучших результатов (при этом оценки bi обладают свойствами состоятельности, несмещенности и эффективности) необходимо выполнение ряда предпосылок относительно случайного отклонения






