Отрицательные числа в ЭВМ представляются в прямом, дополнительном и обратном кодах.
При представлении числа в прямом коде код числа в разрядной сетке из n разрядов совпадает с самим числом.
В двоичной системе счисления знаки кодируются следующим образом: «+» цифрой 0, «-«цифрой 1. Знаковый разряд располагается слева от значащих цифр числа, то есть это крайний левый разряд в представление числа. При таком подходе введение знакового разряда уменьшает диапазон представления положительных и отрицательных чисел. Вес знакового разряда соответствует весу старшего разряда разрядной сетки. Значащие разряды числа занимают n-1 разряд. Диапазон представления положительных чисел 0 
X 
2n-1 –1, а отрицательных 0 X -(2n-1 – 1).
X, при X ³ 0
[X] пр = (7)
q n-1 +lXl, при X £ 0
где q n-1 величина, равная весу старшего разряда (для дробных чисел q n-1 =1).
Обратите внимание на то, что запись числа в форме (7) приводит к двум равнозначным формам записи нуля – «положительной» и «отрицательной».
Примеры: представить в прямом коде следующие числа:
1. а) Х1 = +110112; б) Х3 = +0.110112
Х2 = -110112; Х4 = -0.110112
2. а) Х1 = +7318; б) Х3 = +0.7318
Х2 = -7318; Х4 = -0.7318
3. а) Х1 = +В13; б) Х3 = +0.В13
Х2 = -В13; Х4 = -0.В13
Ответы:
1. qn-1 = 25 = 100000
а) [X1] пр = 0 11011, [X2] пр = 1 11011
Здесь и далее знаковый разряд будет отмечаться подчёркиванием.
б) [X3] пр = 0. 11011
[X4] пр = 1. 11011
Точка в результате используется нами только для указания того, что число представлено правильной дробью и, следовательно, всегда меньше 1. Этот знак не является частью числа и в машинном представлении опускается.
2. qn-1 = 83 = 1000
а) [X1] пр = 0.731 б) [X3] пр = 0.731
[X2] пр = 1.731 [X4] пр = 1.731
3. q n-1 = 163 = 1000
а) [X1] пр = 0.B13 б) [X3] пр = 0.B13
[X2] пр = 1.B13 [X4] пр = 1.В13
Дополнительный код отрицательного числа представляет собой дополнение модуля исходного числа Х до q n, где n - количество разрядов целой части числа Х. Для правильной дроби q n= 10 в соответствующей системе счисления.
Поэтому для целого числа:
 |
Х, при Х>=0
[X] доп = (8)
q n -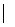 
X 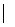, при X<0
Для правильной дроби:
 |
Х, при Х>=0
[X] доп = (9)
1- 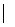X 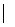, при X<0
Дополнительный код очень удобен при сложении чисел со знаком и вычитании. Действительно, если для трёхразрядного положительного числа B в любой системе счисления дополнение равно B доп= 1000 - 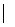B 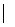, то разность
A – B = A + {1000 - 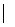B 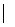} – 1000 = A + B доп –1000.
Таким образом, вычитание сводится к сложению с дополнением вычитаемого. Единица, возникающаая за пределами разрядной сетки за счёт вычитания 1000 должна быть отброшена.
Старший разряд двоичного числа в дополнительном коде имеет смысл знакового разряда. Его нулевое значение соответствует положительному числу, а единичное – отрицательному.
Перевод в дополнительный код для двоичной системы счисления может быть выполнен по следующему правилу: все разряды двоичного числа, включая знаковый, инвертируются и к результату прибавляется единица младшего разряда.
Пример ы: перевести в дополнительный код следующие числа:
1. а) Х1 = +11011; Х2 = -(X1); б) Х3 = +0.11011; Х4 = -(X3);
2. а) Х1 = +731; Х2 = -(X1); б) Х3 = +0.731; Х4 = -(X3);
3. а) Х1 = +В13; Х2 = -(X1); б) Х3 = +0.В13; Х4 = -(X3);
Ответы:
1. q n = 26 = 1000000
а) [X1]доп= 0 11011; [X2] доп =1000000 – 011011= 100101;
или [X2] доп = 100100 + 000001 = 1 00101;
б) [X3] доп = 0.11011 [X4] доп = 10.00000 – 0.11011 = 1. 00101;
или [X4] доп = 1.00100 + 0.000001 = 1. 00101
2. q n = 84 = 10000
а) [X1] доп = 0 731; [X2] доп =10000 – 0731= 7 047;
б) [X3] доп = 0.731 [X2] доп =1.0000 – 0.731= 7. 047;
3. q n+1 = 164 =1 0000
а) [X1] доп = 0.0В13
[X2] доп = 1.F4ЕС + 0.0001 = 1.F4ED
б) [X3] доп = 0.B13
[X4] доп = 1.4ЕС + 0.001 = 1.4ED
Обратный код отрицательных чисел представляется как дополнение модуля исходного целого числа Х до q n+1 и модуля исходной правильной дроби до 1 0 в соответствующей СС без единицы младшего разряда числа.
Если к представлению исходного числа в обратном коде прибавить единицу младшего разряда, то получим исходное число в дополнительном коде.
