РАБОЧАЯ ТЕТРАДЬ
По
Начертательной геометрии
(спецразделы)
Часть 1
ПЕРСПЕКТИВА И ТЕНИ
САРАНСК
ЛИНЕЙНАЯ ПЕРСПЕКТИВА.
1.1. Аппарат линейной перспективы. Перспектива точки
Перспектива прямой линии
Для построения 
перспективы отрезка достаточно найти перспективу двух любых его точек (рис.1.2).
|
При построении перспективы прямой часто используются характерные точки: начало прямой (точка пересечения прямой с картинной плоскостью) N и перспективу F бесконечно удаленной от картины точки прямой. Перспектива основания начала прямой лежит на основании картины, а перспектива основания бесконечно удаленной точки прямой на линии горизонта.
Плоское изображение перспективы прямой линии показано на рис. 1.3.
 |
Прямые общего положения делятся на две группы: 1) восходящие прямые – это прямые, которые по мере удаления от картинной плоскости поднимаются вверх; 2) нисходящие прямые при удалении от картинной плоскости уходят вниз. Расположение прямой в пространстве можно установить по положению перспективы бесконечно удаленной точки прямой (F). Если точка F находится выше линии горизонта, то прямая восходящая (рис. 1.3). У нисходящей прямой (рис. 1.4) точка F ниже линии горизонта (отрезок КМ). У прямой, параллельной предметной плоскости (отрезок СD), перспектива бесконечно удаленной точки находится на линии горизонта, а у прямой (EL), перпендикулярной картине – совпадает с главной точкой картины. На рис. 1.5 приведены перспективные изображения прямых частного положения: АВ || П¢; CD| | П', || П1; EL ^ П1.
Взаимное расположение прямых
На рис. 1.6 по характерным точкам построены перспективы двух восходящих параллельных прямых (а и b). Чтобы определить начала прямых, их продлили до пересечения с картинной плоскостью (точки N). Для нахождения перспективы бесконечно удаленных точек прямых (F) из точки зрения S проведен луч параллельно данным прямым. Соединив прямыми точки N с точкой F, получили перспективы прямых а и b. Как видно из рисунка точка F является общей для обеих прямых. Следовательно, если прямые в пространстве параллельны, то их перспективы сходятся в одной общей точке, называемойточкой схода параллельных прямых. Точка схода у горизонтальных прямых располагается на линии горизонта, а у прямых, перпендикулярных к картине, совпадает с главной точкой
 |
Р. Прямые, параллельные картине, в перспективе остаются параллельными.
Выбор положения картинной плоскости, точки и угла зрения
Обычно перспективу объекта строят по его заданным ортогональным проекциям. Для получения удачного перспективного изображения объекта следует учитывать ряд общих практических рекомендаций (рис. 1.7).
1. Картинная плоскость П¢ может проходить через одно ребро объекта или через несколько ребер, пересекать объект, быть расположенной перед или сзади объекта. Предпочтение следует отдать плоскости, пересекающей объект, т.к. в этом случае элементы, через которые проходит плоскость картины изображаются на ней без искажения.
2. Угол между картинной плоскостью и плоскостью главного фасада a должен выбираться в пределах 25° – 35°.
3. Точку зрения необходимо выбрать такую, которая наиболее полно выявляла форму объекта. При этом угол зрения j между крайними проецирующими лучами, направленными на объект должен быть в пределах 20° – 50°. Оптимальное значение 30°. Точка зрения выбирается также с учетом места, откуда данный объект будет обозреваться большим количеством наблюдателей.
4. Положение главного луча связывают с конкретной композицией объекта. Например, при симметричной композиции главный луч рекомендуется направлять на середину объекта. При этом главный луч должен располагаться в средней трети угла зрения.
5. Высота горизонта h выбирается на уровне глаз человека, расположенного на предметной плоскости. При изображении высотного здания, линия горизонта может располагаться на 1¤3 высоты здания.
 |
Как было отмечено выше, существует несколько способов построения перспективных изображений. В каждом конкретном случае следует выбирать наиболее рациональный. Рассмотрим способ, который широко распространен в практике архитектурно-строительного проектирования зданий и сооружений.
Способ архитекторов
Этот способ основан на свойстве горизонтально расположенных и параллельных между собой прямых сходиться в перспективе в одной общей точке, находящейся на линии горизонта.
1.5.1. Построение перспективы плоской фигуры.
Построение перспективы объекта обычно начинают с построения перспективы его основания. Поэтому сущность этого способа здесь рассматривается вначале на примере построения перспективы плоской фигуры. На рис. 1.8 изображены ортогональные проекции фигуры. Учитывая вышеприведенные рекомендации, на фронтальной проекции (фасаде) проводим линию горизонта, а на горизонтальной проекции (плане) определяем положения основания картинной плоскости, точки зрения S и главной точки картины P. Как видно из чертежа рассматриваемая фигура ограничена горизонтальными линиями двух направлений. Для определения их точек схода через точку S1 на плане проводятся прямые соответственно параллельные прямым каждого направления и отмечаются точки пересечения этих прямых со следом картинной плоскости (точки F11 и F12). После этого на чертеже проводятся две горизонтальные линии (основание картины О1 – О2 и линия горизонта h). На линии горизонта отмечается главная точка картины и в соответствии с ортогональным чертежом точки схода перспектив горизонтальных прямых.
 |
Дальнейшее решение задачи сводится к построению перспектив вершин рассматриваемой плоской фигуры. Зная, что перспектива точки находится пересечением перспектив двух прямых, на рисунке перспективы точек построены путем построения перспектив сторон заданного многоугольника. Где точки N01, N02, N03, N04 и N05 – начала прямых, которым принадлежат стороны фигуры.
 |
При построении перспективы больших сложных объектов чаще всего используют лишь одну точку схода (ближайшую к главной точке картины), так как обе точки схода на чертеже, как правило, не помещаются. На рис. 1.9 построена перспектива той же фигуры с использованием одной точки схода. В данном случае перспективы прямых, которым принадлежат стороны АВ, СD и EL, построены по характерным точкам, а вершины А, В, С, D и L – при помощи проецирующих лучей, направленных из точки зрения в данные точки. Отметив точки пересечения горизонтальных проекций лучей со следом картинной плоскости (А0, В0, С0, D0, L0), перенесем их с плана на основание картины и проведем через полученные точки вертикальные прямые до пересечения с ранее построенными перспективами прямых N01 – F,1 N02 - F1 и N03- F1.
В некоторых случаях для построения точек в перспективе выгодно использовать вспомогательные прямые, проходящие через точки в направлении, перпендикулярном к картинной плоскости. Точкой схода таких прямых является главная точка картины. Пример построения дан на рис. 1.10.
 |
Задачи
1.1. Найти начало и бесконечно удаленные точки прямых. Определить положение каждой прямой в пространстве.
 |
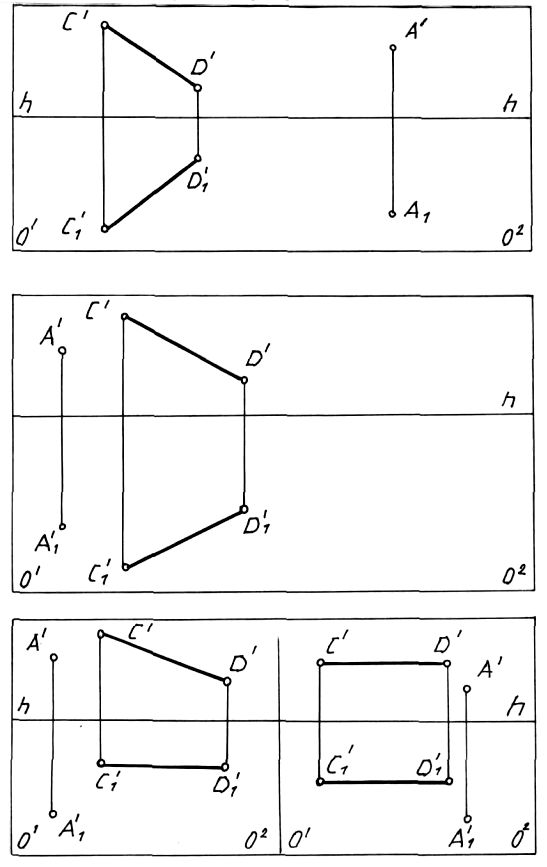1.2. Через точку А провести прямую, параллельную заданной прямой. Определить положение прямых в пространстве.
1.3. Разделить перспективы данных прямых на 4 равные части.
 |
 |
1.4. Произвести разбивку оконных и дверных проемов на перспективеплоскости стены в соответствии с фасадом.
    
|
 1.5. Построить перспективу конуса, пользуясь главной точкой картины
|
1.6. Построить перспективу части стены с козырьком и дверным проемом.
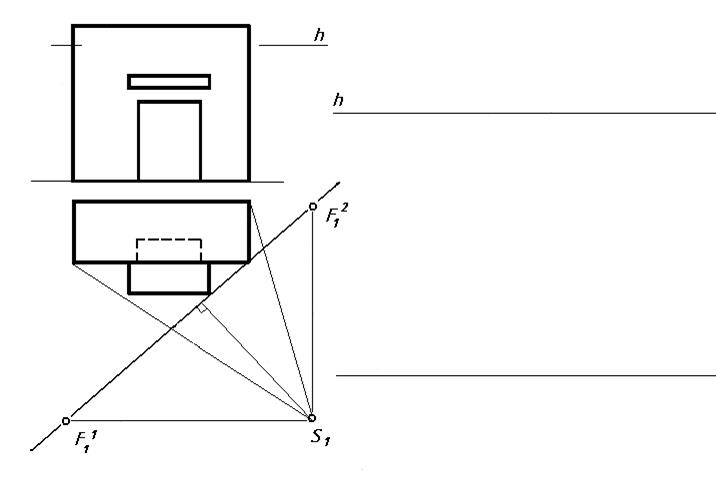
1.7.Построить перспективу лестницы, задавшись положением картины и точки зрения.
1.8. По ортогональным проекциям способом архитекторов построить перспективу здания.
