 |
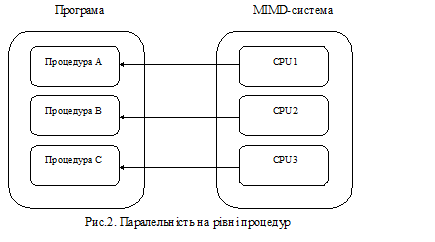
Арифметичні вирази виконуються паралельно покомпонентно, причому в суттєво простіших синхронних методах. Якщо, наприклад, йдеться про арифметичний вираз складання матриць (рис.3.), то він синхронно розпаралелюється дуже просто тому, що кожному процесорові підпорядковується один елемент матриці.
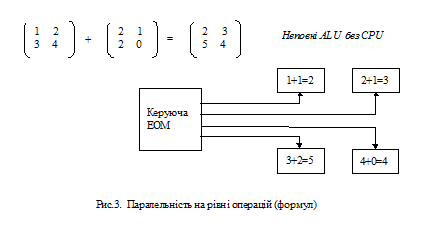 |
При застосуванні n*n процесорних елементів можна одержати суму двох матриць порядку n*n за час виконання однієї операції складання (за винятком часу, потрібного на зчитування та запис даних). Цьому рівню притаманні засоби векторизації та так званої паралельності даних. Останнє поняття пов'язане з детальністю розпаралелювання, а саме - з його поширенням на оброблювані дані. Майже кожному елементу даних тут підпорядковується свій процесор, завдяки чому ті дані, що в машині фон Ноймана були пасивними. перетворюються на “активні обчислювальні пристрої”.
Рівень двійкових розрядів
На цьому piвні відбувається паралельне виконання бітових операцій в межах одного слова. Паралельність на рівні бітів можна знайти в будь-якому працюючому мікропроцесорі. Наприклад, у 8-розрядному арифметико-логічному пристрої побітова обробка виконується паралельними апаратними засобами.
Паралельні операції
Зовсім інший образ паралельності виникає з аналізу математичних операцій над окремими елементами даних або над групами даних. Розрізняють скалярні дані, операції над якими виконуються послідовно, i векторні дані, над якими можна виконати потрібні математичні операції паралельно. Операції, які нижче розглядаються, є основними функціями, що реалізуються у векторних та матричних ЕОМ.
Прості операції над векторами, наприклад складання двох векторів, можуть бути виконані безпосередньо синхронно i паралельно. У цьому випадку можна кожному елементу вектора підпорядкувати один процесор. При складніших операціях, таких як формування Bcix часткових сум, побудова ефективного паралельного алгоритму є не зовсім очевидною справою. Далі розрізняються одномісцеві (монадні) та двомісцеві (діадні) операції i до кожного типу операції наведено характерні приклади.
Одномісцеві операції
а). Скаляр –> скаляр Послідовне виконання
Приклад 9‑>3 "Корінь"
б). Скаляр ‑> вектор Розмноження числової величини
Приклад 9‑>(9,9,9,9) "Broadcast"
в). Вектор ‑> скаляр Редукція вектора в скаляр
Приклад (1,2,3,4)‑>10 "Складання"
(із спрощувальним припущенням, що довжина вектора не змінюється)
г-1) Локальна векторна покомпонентна операція.
Приклад: (1,4,9,16) ‑>•(1,.2,3,4) "Корінь"
г-2) Глобальна векторна операція з перестановками.
Приклад: (1,2,3,4) ‑>• (2,4,3,і) "Заміна місць компонент вектора"
г-3) Глобальна векторна операція (часто складається з простих операцій)
Приклад: (і,2,3,4) ‑> (1,3,6,10) "Часткові суми"
Двомісцеві операції
д) (скаляр, скаляр)‑> вектор Послідовне виконання
Приклад: (1,2)‑>3 Скалярне складання"
е) (скаляр, вектор)‑>вектор Покомпонентне застосування операцій над скаляром i вектором
Приклад: (3,(1,2,3,4))‑>(4,5,6,7) "Складання скаляра з вектором";
операція виконується як послідовність операцій б) та є)
складання векторів:
(3,3,3,3)
+
(1,2,3,4)
3‑>(4,5,6,7)
є) (вектор, вектор) ‑> вектор Покомпонентне застосування операції над двома векторами
Приклад: ((1,2,3,4),(0,і,3,2)) ‑> (1,3,6,6) "Складання векторів"
Покажемо застосування цих операцій на простому прикладі: йдеться про обчислення скалярного добутку двох векторів. Цей результат можна одержати простим послідовним застосуванням базових операцій є) (тут - по-компонентне множення двох векторів) i в) - (редукція одного вектора в один скаляр (тут - за допомогою складання).
Приклад: Скалярний добуток
((1,2,3),(4,2,1))®(4,4,3)® 11






