
Обозначим в правой части этой формулы  через
через  а
а  через
через  .
.
Складывая и вычитая равенства  и
и  находим, что
находим, что 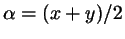 .
.

Подставляя эти выражения в левую часть формулы и читая формулу справа налево, получаем окончательно:

Подставляя в только что полученную формулу  вместо
вместо  , получаем:
, получаем:
Если обработать формулы для  и для
и для  так же, как мы это сделали с формулой для
так же, как мы это сделали с формулой для  , то получится вот что:
, то получится вот что:

| 
| |
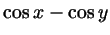
| 
|
Формулы приведения


Методы решения тригонометрических уравнений
Метод замены переменный и подстановки
Решить уравнение 6sin2 x −5sin x +1=0
Решение: Введем новую переменную sin x = t 
 t
t 
 1, получим квадратное уравнение 6 t 2−5 t +1=0. Его корнями являются числа t 1=21
1, получим квадратное уравнение 6 t 2−5 t +1=0. Его корнями являются числа t 1=21  t 2=31. Дданное уравнение сводится к простейшим тригонометрическим уравнениям sin x =217sin x =31. Решая их, находим, что x =(−1) k 6
t 2=31. Дданное уравнение сводится к простейшим тригонометрическим уравнениям sin x =217sin x =31. Решая их, находим, что x =(−1) k 6  +
+  k
k  k
k  Z и x =(−1) n arcsin31+
Z и x =(−1) n arcsin31+  n
n  n
n  Z корни уравнения.
Z корни уравнения.
Метод равенств одноимённых тригонометрических функций.
Решить уравнение sin  6 x −3
6 x −3 
 =sin
=sin  2 x +4
2 x +4 

Решение: Уравнение имеет решение тогда и только тогда, когда 6 x −3  =(−1) k
=(−1) k  2 x +4
2 x +4 
 +
+  k
k  k
k  Z. Решая это уравнение, находим x =6−
Z. Решая это уравнение, находим x =6−  −1
−1 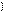 k 23
k 23  +
+  −1
−1 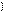 k 4
k 4  +
+  k
k  k
k  Z. Если k = 2m - четное число, то корень уравнения находят по формуле x 1=748
Z. Если k = 2m - четное число, то корень уравнения находят по формуле x 1=748  +2
+2  m
m  m
m  Z. Если k = 2m + 1 - нечетное число, то корень уравнения находят по формуле x 2=9613
Z. Если k = 2m + 1 - нечетное число, то корень уравнения находят по формуле x 2=9613  +4
+4  t
t  t
t  Z
Z
Замечание. Условия равенств одноименных тригонометрических функций, которые пименяются для решения следующих уравнений:
· sin x =sin y  x =
x = 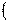 −1
−1  ky +
ky +  k
k  k
k 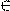 Z
Z
· cos x =cos y  x =
x =  y +2
y +2  k
k  k
k 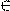 Z
Z
· tgx = tgy  x = y +
x = y +  k
k  k
k 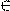 Z
Z
Метод разложение на множители
Решить уравнение cos2 x +sin x  cos x =1
cos x =1
Решение: cos2 x +sin x  cos x =1
cos x =1  cos2 x +sin x
cos2 x +sin x  cos x −cos2 x −sin2 x =0
cos x −cos2 x −sin2 x =0  sin x
sin x  cos x −sin2 x =0
cos x −sin2 x =0  sin x
sin x  cos x −sin x
cos x −sin x  =0
=0 
 sin x =0
sin x =0  cos x −sin x =0
cos x −sin x =0 

 sin x =0
sin x =0  tgx =1
tgx =1 

 x =
x =  n
n  n
n  Z
Z  x =4
x =4  +
+  k
k  k
k  Z
Z  .
.
Метод приведение к однородному уравнению
Решить уравнение 3sin x +4cos x =1
Решение: Используя формулы двойного угла и основное тригонометрическое тождество, приводим данное уравнение к половинному аргументу: 3  2sin x 2cos x 2+4cos2 x 2−4sin2 x 2=sin2 x 2+cos2 x 2. После приведения подобных слагаемых имеем: 5sin2 x 2−6sin x 2
2sin x 2cos x 2+4cos2 x 2−4sin2 x 2=sin2 x 2+cos2 x 2. После приведения подобных слагаемых имеем: 5sin2 x 2−6sin x 2  cos x 2−3cos2 x 2=0. Разделив однородное последнее уравнение на cos2 x 2
cos x 2−3cos2 x 2=0. Разделив однородное последнее уравнение на cos2 x 2  =0, получим 5 tg 2 x 2−6 tgx 2−3=0. Введем новую переменную tgx 2= t, получим квадратное уравнение5 t 2−6 t −3=0, корнями которого являются числа t 1
=0, получим 5 tg 2 x 2−6 tgx 2−3=0. Введем новую переменную tgx 2= t, получим квадратное уравнение5 t 2−6 t −3=0, корнями которого являются числа t 1  2=53
2=53 
 24 Таким образом tg 2 x 1=53−2
24 Таким образом tg 2 x 1=53−2  6и tg 2 x 2=53+2
6и tg 2 x 2=53+2  6. Общее решение можно записать так x 1
6. Общее решение можно записать так x 1  2=2 arctg 53
2=2 arctg 53  2
2  6+2
6+2  k
k  k
k  Z
Z
Замечание. Выражение cos2 x 2 обращается в нуль при x 2=2  +
+  k
k  k
k 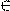 Z, т.е. при x =
Z, т.е. при x =  +2
+2  k
k  k
k 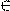 Z. Полученное нами решение уравнения не включает в себя данные числа.
Z. Полученное нами решение уравнения не включает в себя данные числа.
Метод применения свойств функций
Решить уравнение cos x +sin x 4=2
Решение: Так как функции cos x и sin x 4 имеют наибольшее значение, равное 1, то их сумма равна 2, если cos x =1 и sin x 4=1, одновременно, то есть  cos x =1; sin x 4=1
cos x =1; sin x 4=1 

 x =2
x =2  k
k  k
k  Z; x =2
Z; x =2  +8
+8  m
m  m
m  Z
Z 
 x =2
x =2  +8
+8  n
n  n
n  Z
Z
Свойства функций
Определение 1.
Функцию у = f(х) называют возрастающей на множестве X с D(f), если для любых двух точек х1 и х2множества X, таких, что х1 < х2, выполняется неравенство f(х1 < f(х2).
Определение 2.
Функцию у = f(х) называют убывающей на множестве X с D(f), если для любых монотонность двух точек х1 и х2 множества X, таких, что х1 < х2, функции выполняется неравенство f(x1) > f(x2).
На практике удобнее пользоваться следующими формулировками: функция возрастает, если большему значению аргумента соответствует большее значение функции; функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Определение 3.
Функцию у — f(х) называют ограниченной снизу на множестве X с D (f), если все значения функции на множестве X больше некоторого числа (иными словами, если существует число m такое, что для любого значения х є X выполняется неравенство f(х) >m).
Определение 4.
Функцию у = f(х) называют ограниченной сверху на множестве X с D (f), если все значения функции меньше некоторого числа (иными словами, если существует число М такое, что для любого значения х є X выполняется неравенство f(х) < М).
Если множество X не указано, то подразумевается, что речь идет об ограниченности функции снизу или сверху во всей области определения.
Если функция ограничена и снизу, и сверху, то ее называют ограниченной.
Определение 5.
Число m называют наименьшим значением функции у = f(х) на множестве X С D(f), если:
1) в Х существует такая точка х0, что f(х0) = m;
2) для всех x из X выполняется неравенство m>f(х0).
Определение 6.
Число М называют наибольшим значением функции у = f(x) на множестве X С D(f), если:
1) в Х существует такая точка х0, что f(x0) = М;
2) для всех x из X выполняется неравенство 
1. Постоянная функция у = С
График функции у = С изображен на рис. 61 — прямая, параллельная оси х. Это настолько неинтересная функция, что нет смысла перечислять ее свойства.
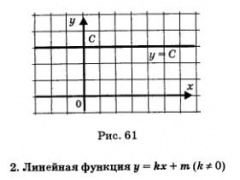
Графиком функции у = кх + m является прямая (рис. 62, 63).
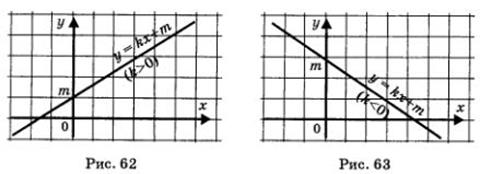
Свойства функции у = кх + m:
1) 
2) возрастает, если к > 0 (рис. 62), убывает, если к < 0 (рис. 63);
3) не ограничена ни снизу, ни сверху;
4) нет ни наибольшего, ни наименьшего значений;
5) функция непрерывна;
6) 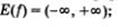
7) о выпуклости говорить не имеет смысла.

Графиком функции у = кх2 является парабола с вершиной в начале координат и с ветвями, направленными вверх, если к > О (рис. 64), и вниз, если к < 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.

Свойства функции у - кх2:
Для случая к> 0 (рис. 64):
1) D(f) = (-оо,+оо);
2) убывает на луче (-оо, 0], возрастает на луче [0, +оо);
3) ограничена снизу, не ограничена сверху;
4)  =
=  не существует;
не существует;
5) непрерывна;
6) Е(f) = [0,+оо);
7) выпукла вниз.
Обратите внимание: на промежутке (-оо, 0] функция убывает, а на промежутке [0, +оо) функция возрастает. Эти промежутки называют промежутками монотонности функции у = кх2. Понятие промежутка монотонности будем использовать и для других функций.
Для случая к < 0 (рис. 65):
1) D(f) = (-оо,+00);
2) возрастает на луче (-оо, 0], убывает на луче [0, +оо);
3) не ограничена снизу, ограничена сверху;
4)  не существует,
не существует,  = 0;
= 0;
5) непрерывна;
6) Е(f) > = (-оо, 0];
7) выпукла вверх.
График функции у = f(х) строится по точкам; чем больше точек вида (х; f(х)) мы возьмем, тем более точное представление о графике получим. Если этих точек взять достаточно много, то и представление о графике сложится более полное. Именно в этом случае интуиция и подсказывает нам, что график надо изобразить в виде сплошной линии (в данном случае в виде параболы). А уж затем, читая график, мы делаем выводы о непрерывности функции, о ее выпуклости вниз или вверх, об области значений функции. Вы должны понимать, что из перечисленных семи свойств «законными» являются лишь свойства 1), 2), 3), 4) — «законными» в том смысле, что мы в состоянии обосновать их, ссылаясь на точные определения. Об остальных свойствах у нас имеются только наглядно-интуитивные представления. Кстати, в этом нет ничего плохого. Из истории развития математики известно, что человечество часто и долго пользовалось различными свойствами тех или иных объектов, не зная точных определений. Потом, когда такие определения удавалось сформулировать, все становилось на свои места.

Графиком функции является гипербола, оси координат служат асимптотами гиперболы (рис. 66, 67).

1) D(f) = (-00,0)1U (0,+оо);
2) если к > 0, то функция убывает на открытом луче (-оо, 0) и на открытом луче (0, +оо) (рис. 66); если к < 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) не ограничена ни снизу, ни сверху;
4) нет ни наименьшего, ни наибольшего значений;
5) функция непрерывна на открытом луче (-оо, 0) и на открытом луче (0, +оо);
6) Е(f) = (-оо,0) U (0,+оо);
7) если к > 0, то функция выпукла вверх при х < 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х > 0, т.е. на открытом луче (0, +оо) (рис. 66). Если к < 0, то функция выпукла вверх при х > О и выпукла вниз при х < О (рис. 67).
5. Функция 
Графиком функции является ветвь параболы (рис. 68). Свойства функции  :
:
1) D(f) = [0, +оо);
2) возрастает;
3) ограничена снизу, не ограничена сверху;
4)  =
=  не существует;
не существует;
5) непрерывна;
6) Е(f) = [0,+оо);
7) выпукла вверх.
6. Функция у = | х |
Графиком функции является объединение двух лучей:
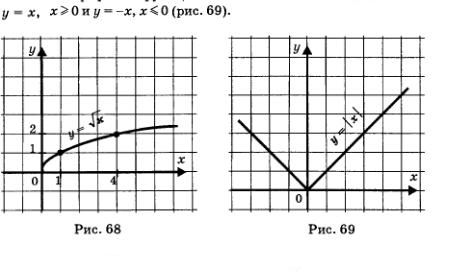
Свойства функции у= | х |:
1) D(f) = (-оо,+оо);
2) убывает на луче (-оо, 0], возрастает на луче [0, +оо);
3) ограничена снизу, не ограничена сверху;
4)  =
=  не существует;
не существует;
5) непрерывна;
6) Е(f) = [0,+оо);
7) функцию можно считать выпуклой вниз.
7. Функция у = ах2 + Ьх + с
Графиком функции является парабола с вершиной в точке 
и с ветвями, направленными вверх, если а > 0 (рис. 70), и вниз,
если а < 0 (рис. 71). Прямая  является осью параболы.
является осью параболы.

Область определения функции — множество, на котором задаётся функция.
Область значений функции — множество значений, которые принимает функция в результате ее применения.
Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.
Свойства функции у = logaх, a > 1:
|
логарифмическая функция ее свойства и график
График логарифмической функции log aх можно построить, воспользовавшись тем, что функция log aх обратна показательной функции y = ax. Поэтому достаточно построить график функции y = ax, а затем отобразить его симметртрично относительно прямой у = х.
Свойства функции у = l ogaх, 0 < a < 1:
- D(f) = (0;+
 );
); - не является ни четной, ни нечетной;
- убывает на (0; +
 );
); - не ограничена сверху, не ограничена снизу;
- нет ни наибольшего, ни наименьшего значений;
- непрерывна;
- E(f) = (-;
 +
+  );
); - выпукла вниз;
- дифференцируема.
Свойства функции у = ln х:
- D(f) = (0; +
 );
); - не является ни четной, ни нечетной;
- возрастает на {0; +
 );
); - не ограничена сверху, не ограничена снизу;
- не имеет ни наибольшего, ни наименьшего значений;
- непрерывна;
- E(f) = (-
 ;+
;+  );
); - выпукла вверх;
- дифференцируема.

Показательная функция — математическая функция  , где
, где  называется основанием степени, а
называется основанием степени, а  — показателем степени.
— показателем степени.
1. Область определения — множество R действительных чисел.
2. Область значений — множество R+ всех положительныхдействительных чисел.
3. При а > 1 функция возрастает на всей числовой прямой; при 0<а<1 функция убывает на множестве R.
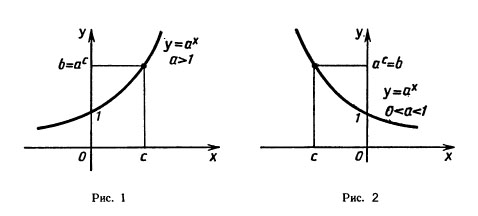
Графики показательных функций для случаев а>\ и 0<1<1 изображены на рисунках 1-2.
4. При любых действительных значениях х и у справедливы равенства
аxаy = аx+y; 
(ab)x = axbx; 
(ax)y = аxy.
Эти формулы называют основными свойствами степеней.
Свойства 3 и 4 означают, что для функции у = аx, определенной на всей числовой прямой, остаются верными свойства функции y = аx, которая сначала была определена только для рациональных х.
Степенна́я фу́нкция — функция  , где
, где  (показатель степени) — некоторое вещественное число[1]. К степенным часто относят и функцию вида
(показатель степени) — некоторое вещественное число[1]. К степенным часто относят и функцию вида  , где k — некоторый масштабный множитель.[2] Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда является целым или рациональным числом
, где k — некоторый масштабный множитель.[2] Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда является целым или рациональным числом






