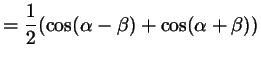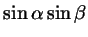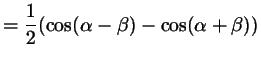Умножение комплексных чисел
Настал момент познакомить вас со знаменитым равенством:
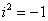
Пример 3
Найти произведение комплексных чисел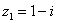 
, 
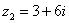
Очевидно, что произведение следует записать так:
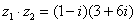
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что 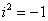и быть внимательным.
Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
Я распишу подробно:
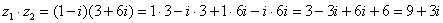
Надеюсь, всем было понятно, что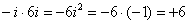 
Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках.
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: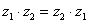 
.
В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.
Деление комплексных чисел
Пример 4
Даны комплексные числа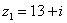 
, 
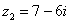. Найти частное 
.
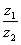Составим частное:
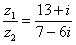
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем бородатую формулу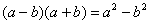 
и смотрим на наш знаменатель: 
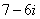. В знаменателе уже есть 
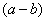, поэтому сопряженным выражением в данном случае является 
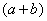, то есть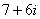 
Согласно правилу, знаменатель нужно умножить на 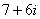, и, чтобы ничего не изменилось, домножить числитель на то же самое число :
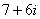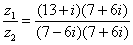
Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой 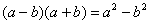(помним, что 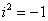и не путаемся в знаках!!!).
Распишу подробно:
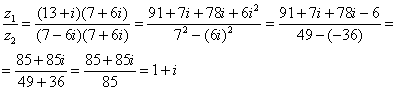
Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде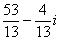 
.
В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: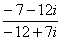 
. Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: 
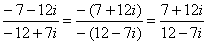. Для любителей порешать приведу правильный ответ: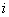 
Абсолютная погрешность - это разница между результатом измерения Xизм и истинным (действительным) значением Xд измеряемой величины.
Относительная погрешность - это отношение абсолютной погрешности измерения к действительному значению измеряемой величины.
ЛОГАРИФМ.
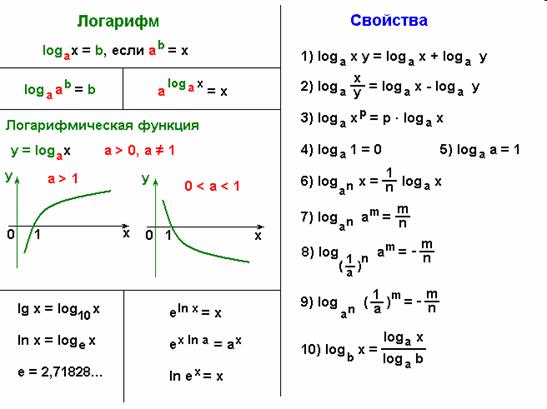
Логарифмом числа b по основанию a (b > 0, a > 0, a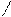 
=1 ) называют показатель степени, в который нужно возвести число a, чтобы получить число b:
alogab = b
Рассмотрим утверждения и правила, позволяющие решить уравнения.
Представим: loga x = b - это простейший вид логарифмического уравнения.
Если a > 0, a ≠ 1, то можно смело утверждать, что уравнение при любом значение b имеет решение x = a^b (a в степени b).
Помните свойства логарифмической функции, что помогут при решении:
1) Область определения - множество только положительных чисел.
2) Область значения - множество действительных чисел.
3) Если a > 1 логарифмическая функция строго возрастает, в обратном случае - строго убывает.
4) loga 1 = 0 и loga a = 1, следует учесть, что a > 0, a ≠ 1.
5) И последнее - Если a > 1, то функция выпукла вверх.
При решение логарифмических уравнений лучше использовать равносильное преобразование. Учитывайте преобразования, которые могут привести и к потере корней. Используйте определения и все свойства логарифма при решении.
Также можно использовать метод подстановки. Метод позволяет заменять логарифм другим значением, например - t, после решения восстановив логарифм.
Напишем одну под другой формулы синуса суммы и синуса разности:
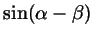
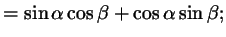
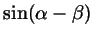
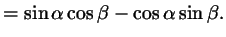
Сложив эти формулы, получим
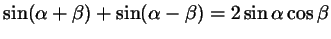или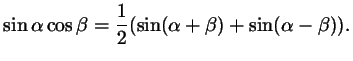 
Поступая аналогичным образом с формулами косинуса суммы и разности, получим:
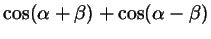
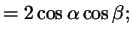
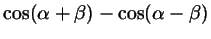
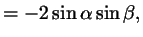
откуда получаются такие формулы:
