Вычисление двойного интеграла

Пусть обл.D-правильная в направлении оси OY

D={(x,y):a£x£b,j₁(x)<y<j₂(x)}

Через произвольную точку xÎ[a,b] проведем плоскость ^ оси OX.В результате такого построения криволинейный цилиндр получит сечение,изображенное на рисунке.Это сечение представляет собой криволинейную трапецию,ограниченную снизу отрезком AB,а сверху кривой,лежащей на поверхности f(x,y)

Вспомним вычисление объема тела по заданному поперечному сечению.

V=_Aò^BS(x)dx,где S-площадь сечения.

Найдем площадь полученного сечения.Используем формулу площади криволинейной трапеции.Во всех точках сечения x-постоянная.

Тогда S(x)=_j₁(x)ò^j²(x)f(x,y)dy

Подставляем формулу площади в формулу объема в итоге получаем:V=_aò^bdx_j₁₍_x₎ò^j²⁽^x⁾f(x,y)dy

Сравнивая объем тела,полученного через площадь поперечного сечения с объемом двойного интеграла,мы приходим к формуле:

ò_Dòf(x,y)dS=_aò^bdx_j_1(x)ò^j^2(x)f(x,y)dy (1)

Пусть обл.D-правильная и в направлении оси OX

D={(x,y):0£y<d_i,j₁(y)£x£j₂(y) через произвольную точку yÎ[0;d] проведем плоскость^оси OY.

S(y)=_j_1(y)ò^j^2(y)f(x,y)dx

ò_Dòf(x,y)dS=₀ò^ddy_j_1(y)ò^j^2(y)f(x,y)dx (2)

Сравнивая 2 полученные формулы,олучаем:

_aò^bdx_j₁₍_x₎ò^j²⁽^x⁾f(x,y)dy=₀ò^ddy_j₁₍_y₎ò^j²⁽^y⁾f(x,y)dx-формула изменения порядка интегрирования.

В правых частях формул (1) и (2) стоят интегралы,которые называются повторными интегралами.

Правило вычисления повторного интеграла:

1.первым вычисляется интеграл,стоящий справа(внутренний интеграл),как обычный определенный интеграл по той переменной,которая стоит после дифференциала,считая вторю переменную постоянной.

2.После вычисления внутреннего интеграла вычисляется внешний.

Изменение порядка интегрирования в повторном интеграле.

Пусть обл.D-правильная в направлении оси OY

D={(x,y):a£x£b,j₁(x)<y<j₂(x)}

Вспомним вычисление объема тела по заданному поперечному сечению.

V=_Aò^BS(x)dx,где S-площадь сечения.

Тогда S(x)=_j₁(x)ò^j²(x)f(x,y)dy

Подставляем формулу площади в формулу объема в итоге получаем:V=_aò^bdx_j₁₍_x₎ò^j²⁽^x⁾f(x,y)dy

ò_Dòf(x,y)dS=_aò^bdx_j_1(x)ò^j^2(x)f(x,y)dy (1)

Пусть обл.D-правильная и в направлении оси OX

D={(x,y):0£y<d_i,j₁(y)£x£j₂(y) через произвольную точку yÎ[0;d] проведем плоскость^оси OY.

S(y)=_j_1(y)ò^j^2(y)f(x,y)dx

ò_Dòf(x,y)dS=₀ò^ddy_j_1(y)ò^j^2(y)f(x,y)dx (2)

Сравнивая 2 полученные формулы,олучаем:

_aò^bdx_j₁₍_x₎ò^j²⁽^x⁾f(x,y)dy=₀ò^ddy_j₁₍_y₎ò^j²⁽^y⁾f(x,y)dx-формула изменения порядка интегрирования.

В правых частях формул (1) и (2) стоят интегралы,которые называются повторными интегралами.

Тройной интеграл.

Предел при r®0 интегральных сумм, не зависящий от способа разбиения области V, называется тройным интегралом от функции f(x, y, z) по области V: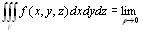

Пусть правильная в направлении Oz область V ограничена непересекающимися поверхностями z=z₁(x,y) и z=z₂(x,y), а с боков – цилиндрической поверхностью F(x,y)=0 с образующими,параллельными оси Oz, т.е. V={(x,y)ÎS,z₁(x,y)£z£z₂(x,y)}, где S-проекция V на плоскость Oxy

{Т}Пусть:1) в области V={(x,y)ÎS,z₁(x,y)£z£z₂(x,y)} задана функция f(x,y,z), интегрируемая по Риману,т.е. существует тройной интеграл òòò_V fdV; 2)существует повторный интеграл ò_SòdS _z₁₍_x_,_y₎ò^z²⁽^x^,^y⁾fdz.Тогда справедлива формула:

òòò_V f(x,y,z)dV=ò_Sòdxdy _z1(x,y)ò^z2(x,y)f(x,y,z)dz. После того как вычислен внутренний интеграл по переменной z(при этом x и y предполагаются постоянными):

_z₁₍_x_,_y₎ò^z²⁽^x^,^y⁾f(x,y,z)dz=G(x,y,z) _z₁₍_x_,_y₎ç^z²⁽^x^,^y⁾=G(x,y,z₂(x,y))-G(x,y,z₁(x,y))=g(x,y). Вычисление тройного интеграла сводится к вычислению двойного интеграла

ò_Sòg(x,y)dxdy