По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице

Построена матрица парных коэффициентов корреляции

На основании сравнения частных F-критериев Фишера (F_табл=5,12) можно утверждать, что фактор …

х₁ целесообразно включать в уравнения регрессии после того, как в него был включен фактор х₂

х₂ целесообразно включать в уравнения регрессии после того, как в него был включен фактор х₁

х₁ нецелесообразно включать в уравнения регрессии после того, как в него был включен фактор х₂

х₂ нецелесообразно включать в уравнения регрессии после того, как в него был включен фактор х₁

Решение:

Частные F-критерии и оценивают статистическую значимость присутствия факторов х₁ и х₂ в уравнении множественной регрессии, оценивают целесообразность включения одного фактора после другого. оценивает целесообразность включения в уравнения факторов х₁ после того, как в него был включен фактор х₂, а указывает на целесообразность включения в модель фактора х₂ после фактора х₁.
Чтобы вычислить коэффициент детерминации, воспользуемся формулой . Будем считать х₁ – доход, х₂ – имущество. Коэффициенты парной корреляции известны и равны ,
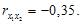
Расчет стандартизированных коэффициентов выполним по формулам
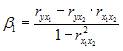= = 0,7236;
= = -0,4467.

Итак, коэффициент детерминации равен
=0,88·0,7236+(-0,7)·(-0,4467)=0,9495.

Частные F-критерии

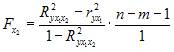= 81,89> F_табл, значит, целесообразно включить в уравнения регрессии фактор х₁ после того, как в него был включен фактор х₂.

= 31,21> F_табл, значит, целесообразно включить в уравнения регрессии фактор х₁ после того, как в него был включен фактор х₂.

В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.

По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R² = 0,9708.

Исключив из выборки аномальное значение (Московскую область) и построив уравнение линейной зависимости, можно утверждать, что …

между объемом кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам, и инвестициями в основной капитал нет линейной зависимости

коэффициент регрессии в полученном уравнении оказался незначимым, значит, его можно признать равным нулю

при увеличении объема кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам на 1 млн руб., инвестиции в основной капитал увеличиваются на 5,3 млн руб.

при увеличении объема кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам на 1 млн руб., инвестиции в основной капитал уменьшаются на 5,3 млн руб.

Решение:

Если исключить аномальное значение и построить поле корреляции и уравнение регрессии, а также рассчитать коэффициент детерминации (см. на рисунке), то можно заметить, что связь между переменными является слабой.

Значит, можно сделать вывод, что между объемом кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам, и инвестициями в основной капитал по Центральному федеральному округу нет линейной зависимости. Кроме того, в уравнении y = 4083,7 + 5,3083 · x коэффициент регрессии b является незначимым и его можно считать равным нулю.

 

Кейс 1 подзадача 4

1. По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x. Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков.

 

Значение критерия Дарбина–Уотсона составит … (Полученное значение округлите до десятых.)

Решение:

Статистика Дарбина–Уотсона вычисляется по формуле , где – коэффициент автокорреляции первого порядка. Поскольку = –0,45539, то статистика Дарбина–Уотсона d = 2 · (1 - (-0,45539)) = 2,9.