(1) 
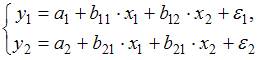
(2) 
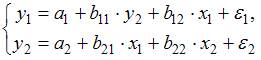
(3) 
система независимых уравнений
система рекурсивных уравнений
система одновременных уравнений
система нормальных уравнений
Решение:
В системе (1) в обоих уравнениях зависимые переменные 
и 
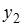зависят только от независимых переменных 
и 
. Это система независимых уравнений.
В системе (2) второе уравнение содержит в правой части только независимые переменные и , а первое уравнение для уже включает в себя и зависимую переменную 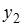, определенную во втором уравнении. Это система рекурсивных уравнений.
В системе (3) зависимые переменные и 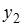содержатся и в правой, и в левых частях уравнения. Это система одновременных уравнений.
Система нормальных уравнений не относится к классу эконометрических уравнений.
4. Установите соответствие между видом и классом системы эконометрических уравнений:
(1) 
(2) 
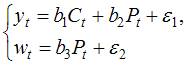
система одновременных уравнений с лаговыми переменными
система независимых уравнений
система одновременных уравнений без лаговых переменных
Решение:
Рассмотрим каждую из систем эконометрических уравнений.
В системе (1) в правой части первого уравнения стоит переменная St, которая во втором уравнении находится в левой части, следовательно, система является системой одновременных уравнений. Во втором уравнении системы (1) одновременно с переменной Pt находится лаговая переменная Pt-1, поэтому система (1) является системой одновременных уравнений с лаговыми переменными.
В системе (2) в левой части представлены переменные yt и wt, которые не входят в правую часть уравнений системы, поэтому система (2) является системой независимых уравнений.
5. Установите соответствие между классом и видом системы эконометрических уравнений:
(1) система одновременных уравнений
(2) система рекурсивных уравнений
(3) система независимых уравнений
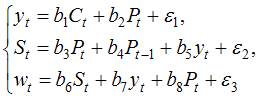
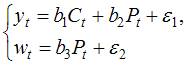
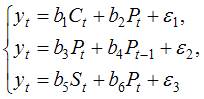
Решение:
Рассмотрим каждую из систем эконометрических уравнений.
(3) – система независимых уравнений. В такой системе в правой части уравнений стоят только независимые переменные, которые не могут находиться в левой части других уравнений системы. Поэтому для системы (3) правильным вариантом ответа является система
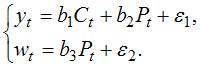
(1) – система одновременных (взаимозависимых) уравнений. В правой части уравнений такой системы одновременно с независимыми переменными стоят и зависимые переменные, которые в других уравнениях находятся в левой части и являются функциями набора зависимых и/или независимых переменных. Порядок следования зависимых переменных y в правой части уравнений не зависит от количества предыдущих уравнений. Поэтому для системы (1) правильным вариантом ответа является система
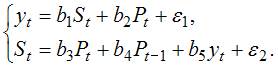
(2) является системой рекурсивных уравнений. В такой системе в правой части уравнений стоят как зависимые, так и независимые переменные; при этом каждое последующее уравнение в правой части включает зависимые переменные y только предыдущих уравнений системы. Поэтому для системы (2) правильным вариантом ответа является система
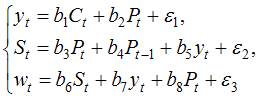
Система 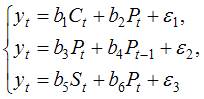содержит ошибку, так как в левой части всех уравнений системы стоит переменная уt. Поэтому данная система не может быть отнесена ни к одному из классов систем эконометрических уравнений.
Тема 23: Идентификация систем эконометрических уравнений
