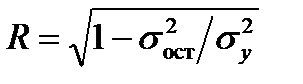o индекса корреляции для исследуемой зависимости близко к 0
o линейного коэффициента корреляции для исследуемой зависимости близко к 1
o доля остаточной дисперсии результативного признака в его общей дисперсии стремится к 1
370. Уравнение нелинейной регрессии 
, где 
– общая дисперсия результативного признака y; 
– остаточная дисперсия ошибки ε, может оцениваться показателем тесноты связи – индексом корреляции R, который вычисляется по формуле …
Тема: Временные ряды данных: характеристики и общие понятия
371. В общем случае каждый уровень временного ряда формируется под воздействием …
- сезонных колебаний и случайных факторов
- случайных временных воздействий
- тенденции и случайных факторов
- тенденции, сезонных колебаний и случайных факторов
372. Временным рядом является …
- значения временных характеристик и соответствующие им значения экономического показателя
- совокупность значений экономического показателя за несколько последовательных моментов (периодов времени)
- совокупность данных, описывающих различные объекты в определённый момент (период) времени
- совокупность временных факторов
373. Временной ряд характеризует …
- зависимость последовательных моментов (периодов) времени
- данные, описывающие совокупность различных объектов в определённый момент (период) времени
- совокупность последовательных моментов (периодов) времени
- данные, описывающие один объект за ряд последовательных моментов (периодов) времени
374. Временной ряд – это совокупность значений экономического показателей …
- за несколько последовательных моментов (периодов) времени
- по однотипным объектам
- за несколько непоследовательных моментов (периодов) времени
- не зависящих от времени
375. Долгосрочную тенденцию изменения признака называют …
o сезонной компонентой
o случайной компонентой
o циклической компонентой
o трендом
376. Значение коэффициента автокорреляции 2-го порядка характеризует связь между …
o двумя временными рядами
o исходными уровнями и уровнями этого же ряда, сдвинутыми на 2 момента времени
o исходными уровнями и уровнями второго временного ряда
o исходными уровнями и уровнями другого ряда, сдвинутыми на 2 момента времени
- Значение коэффициента автокорреляции рассчитывается по аналогии с …
o линейным коэффициентом корреляции
o линейным коэффициентом регрессии
o линейным коэффициентом детерминации
o нелинейным коэффициентом корреляции
378. Модель временного ряда предполагает …
o отсутствие последовательности моментов (периодов) времени, в течение которых рассматривается поведение экономического показателя
o зависимость значений экономического показателя от времени
o пренебрежение временными характеристиками ряда
o независимость значений экономического показателя от времени
379. Основной задачей моделирования временных рядов является …
- исключение значений каждой из трёх компонент из уровней временного ряда
- исключение уровней из совокупности значений временного ряда
- выявление и придание количественного значения каждой из трёх компонент
- добавление новых уравнений к совокупности значений временного ряда
380. Отдельные значения экономической характеристики объекта, полученные в последовательные моменты или периоды времени, называются …
o автокорреляционной функцией
o вариационным рядом
o множественной регрессией
o уровнями временного ряда
381. При моделировании временных рядов экономических показателей необходимо учитывать __________ характер уровней исследуемых показателей.
o стохастический
o конструктивный
o аналитический
o независящий от времени
382. Под трендом временного ряда понимают …
- действия исследователя по приведению исходного временного ряда к стационарному виду
- влияние случайной составляющей на уровень временного ряда
- изменение, определяющее общее направление развития
- влияние циклических колебаний на уровень временного ряда
- Под уровнем временного ряда понимают …
- разницу между максимальным и минимальным значениями ряда
- количество рассматриваемых периодов
- среднее значение временного ряда
- значение временного ряда в конкретный период времени
384. Порядок коэффициента автокорреляции определяется …
o числом уровней временного ряда
o величиной лага
o степенью коэффициента парной линейной корреляции
o числом сравниваемых уровней временного ряда
385. Случайные колебания, радикально меняющие параметры модели или саму модель, называются …
- эволюционными остаточными
- циклическими (конъюнктурными)
- разладочными
- сезонными
386. Среди факторов, оказывающих влияние на уровень временного ряда, можно назвать …
- тенденцию и случайные факторы
- сезонные колебания и тенденцию
- автокорреляцию и тренд
- динамику и совокупные факторы
387. Уровнем временного ряда является …
- среднее значение временного ряда
- совокупность значений временного ряда
- значение конкретного момента (периода) времени
- значение временного ряда в конкретный момент (период) времени
- Уровень временного ряда может формироваться под воздействием тенденции, сезонных колебаний и …
o циклических колебаний
o динамической составляющей
o случайных воздействий
o тренда
389. Уровень временного ряда характеризуется конкретным значением …
- сезонных колебаний временного ряда
- экономического показателя в определённый момент времени
- временного ряда в заданный момент (период) времени
- случайной компоненты временного ряда
- Факторы, описывающие сезонную компоненту временного ряда, могут характеризоваться _____ воздействием на экономический показатель.
- случайным
- долговременным характером
- периодическим
- сезонным
391. Циклическая (конъюнктурная) компонента имеет место во временных рядах, отражающих наблюдения в течение …
- длительного периода времени
- 1 года
- периода меньше 1 года
- одного времени года (зима/весна/лето/осень)
392. Эргодичность временного ряда позволяет …
o использовать выборочные аналоги генеральных характеристик временного ряда для определения его свойств
o использовать МНК для аналитической записи тренда
o выделять сезонные колебания временного ряда
o анализировать свойства остатков временного ряда
Тема: Выявление структуры временного ряда
- Автокорреляционная функция характеризует …
- значения сезонной компоненты временного ряда
- уравнение тренда временного ряда
- зависимость значения коэффициента автокорреляции от его порядка
- значения коэффициентов автокорреляции, которые могут быть отображены на коррелограмме
394. Высокое значение коэффициента автокорреляции порядка L для уровней временного ряда свидетельствует о том, что исследуемый ряд содержит (помимо тенденции) …
- колебания с периодом L
- ярко выраженный тренд
- только случайную компоненту
- разладочную случайную компоненту
- Выявление компонент тренда и сезонных колебаний проводится на основании …
- расчёта и анализа коэффициентов автокорреляции различных порядков
- моделирования систем эконометрических уравнений
- построения и анализа коррелограммы
- исследования многофакторной модели
396. В формуле коэффициента автокорреляции 
, t =1+ L,…, n, величина 
означает …
- средний уровень ряда Xt
- лаг, сдвиг уровней временного ряда
- средний уровень ряда Xt – L
- среднее квадратическое отклонение временного ряда Xt
397. Если наиболее высоким оказался коэффициент автокорреляции 3-го порядка, то исследуемый ряд содержит …
- сезонные колебания с периодичностью в 3 момента времени
- линейный тренд, проявляющийся в каждом 3-м уровне ряда
- нелинейную тенденцию полинома 3-го порядка
- случайную величину, влияющую на каждый 3-й уровень ряда
398. Значение коэффициента автокорреляции второго порядка характеризует связь между …
- исходными уровнями и уровнями второго временного ряда
- двумя временными рядами
- исходными уровнями и уровнями другого ряда, сдвинутыми на 2 момента времени
- исходными уровнями и уровнями этого же ряда, сдвинутыми на 2 момента времени
399. Значение коэффициента автокорреляции рассчитывается по аналогии с …
- линейным коэффициентом регрессии
- нелинейным коэффициентом корреляции
- линейным коэффициентом детерминации
- линейным коэффициентом корреляции
400. Коррелограммой является …
- графическое отображение автокорреляционной функции
- аналитическое выражение для автокорреляционной функции
- графическое отображение регрессионной функции
- процесс экспериментального нахождения значений автокорреляционной функции
- Коэффициент автокорреляции уровней временного ряда характеризует …
- качество построенной модели временного ряда
- тесноту связи между уровнями временного ряда и значениями моментов (периодов) времени
- тесноту линейной связи между уровнями исходного временного ряда и уровнями этого же ряда, сдвинутыми на несколько моментов (периодов)
- значение коэффициента корреляции между двумя рядами, первый из которых – исходный, а второй получен сдвигом исходного ряда на заданное число уровней
402. Порядок коэффициента автокорреляции определяется …
- величиной лага
- числом уровней временного ряда
- степенью коэффициента парной линейной корреляции
- количеством сравниваемых уровней временного ряда
- При выявлении структуры временного ряда проводят анализ …
- графика зависимости значений уровня ряда от времени
- существенности параметров
- матрицы парных коэффициентов линейной корреляции
- автокорреляционной функции
404. Пусть yt = f (T, S, E) – модель временного ряда. Установите соответствие между обозначениями и их интерпретациями.
1. yt
2. T
3. S
4. E
- случайные факторы
- уровень временного ряда в момент времени t
- сезонные колебания
- тенденция ряда
- Совокупность значений коэффициента автокорреляции, соответствующих порядкам для которых они рассчитаны, может быть получена на основе …
- модели временного ряда
- значений факторов, которые формируют уровни временного ряда
- автокорреляционной функции
- коррелограммы
406. Структуру временного ряда можно выявить с помощью коэффициента …
- автокорреляции уровней ряда
- авторегрессии уровней ряда
- регрессии уровней ряда
- автодетерминации уровней ряда
407. Установите соответствие между видом функций временного ряда и его структурой.
1. yt = f (T, E)
2. yt = f (T, S, E)
3. yt = f (S, E)
4. yt = f (E)
- ряд содержит тенденцию и случайную составляющую
- ряд содержит только случайную составляющую
- ряд содержит сезонные колебания и случайную составляющую
- ряд содержит тенденцию, сезонные колебания и случайную составляющую
408. Установите соответствие между значениями коэффициентов автокорреляции различного порядка и возможной структурой временного ряда.
1. высокий коэффициент автокорреляции только 1-го порядка
2. высокий коэффициент автокорреляции 1-го порядка и ( > 2)
3. высокий коэффициент автокорреляции только порядка ( > 2)
4. отсутствуют высокие значения коэффициентов автокорреляции
- ряд содержит тенденцию, сезонные колебания и случайную составляющую
- ряд содержит только случайную составляющую или имеет сильную нелинейную тенденцию
- ряд содержит сезонные колебания и случайную составляющую
- ряд содержит линейную тенденцию и случайную составляющую
409. Установите соответствие между эконометрическими терминами и их определениями.
1. временной ряд
2. порядок коэффициента автокорреляции уровней временного ряда
3. уровень временного ряда
4. автокорреляционная функция
- значение временного ряда в определённый период времени
- ряд значений экономического показателя за несколько последовательных периодов времени
- последовательность коэффициентов автокорреляции 1-го, 2-го и т.д. порядков
- число периодов, на которое сдвигается исходный временной ряд при расчёте значения коэффициента автокорреляции
410. Установите соответствие между эконометрическими терминами и областью их применения.
1. автокорреляционная функция
2. тест Голдфелда–Квандта
3. критерий Дарбина–Уотсона
4. матрица парных коэффициентов корреляции
- служит для выявления структуры временного ряда
- служит для проверки гипотезы о гомоскедастичности остатков
- служит для проверки гипотезы об отсутствии автокорреляции остатков
- служит для оценки мультиколлинеарности факторов
Тема: Аддитивная и мультипликативная модели временных рядов
411. Гипотеза об аддитивной структурной схеме взаимодействия факторов, формирующих уровни временного ряда, 
означает правомерность следующего представления...
- уровень временного ряда = тренд + конъюнктурная компонента + сезонный фактор + случайная компонента
- уровень временного ряда = случайная компонента – тренд + конъюнктурная компонента + сезонный фактор
- тренд = уровень временного ряда + конъюнктурная компонента + сезонный фактор + случайная компонента
- случайная компонента = тренд + конъюнктурная компонента + сезонный фактор + уровень временного ряда
412. Если факторы входят в модель как произведение, то модель называется …
O мультипликативной
o аддитивной
o суммарной
o производной
413. Если факторы входят в модель как сумма, то модель называется …
- производной
- аддитивной
- суммарной
- мультипликативной
414. Известны значения аддитивной модели временного ряда: Yt – значение уровня ряда, Yt =30, T – значение тренда, T =15, Е – значение компоненты случайных факторов E =2. Определите значение сезонной компоненты S.
- S =1
- S =13
- S =–1
- S =0
415. Моделирование тенденции осуществляется на основе построения уравнения регрессии зависимости …
- уровня ряда от времени
- трендовой компоненты от времени
- сезонной компоненты от времени
- случайной компоненты от времени
- Модель временного ряда, имеющая следующую спецификацию Yi = Ti · Si · Ci · εi (где Yi – уровень временного ряда, Ti – тренд, Si – сезонная компонента, εi – случайная компонента), называется …
o смешанной
o аддитивной
o мультипликативной
o нелинейной
417. Модель временного ряда, имеющая следующую спецификацию Yt = Tt · St + Ct + Et (где Yt – уровень временного ряда, Tt – тренд, St – сезонная компонента, Ct – конъюнктурная компонента, Et – случайная компонента), называется …
- смешанной
- мультипликативной
- аддитивной
- нелинейной
418. Параметры уравнения тренда определяются ________ методом наименьших квадратов
- обычным
- двухшаговым
- косвенным
- обобщённым
419. Построена аддитивная модель временного ряда, где Yt – значение уровня ряда, Yt =10, T – значение тренда, S – значение сезонной компоненты, E – значений случайной компоненты. Определите вариант правильно найденных значений компонент уровня ряда.
- T =7, S =5, E =2
- T =5, S =2, E =1
- T =5, S =2, E =0
- T =5, S =2, E =3
420. Пусть Xt – значения временного ряда с квартальными наблюдениями, St –мультипликативная сезонная компонента, причём для второго квартала года St = S 2=6, для третьего квартала года 
, для четвёртого квартала года St = S 4=2. Определите оценку сезонной компоненты для первого квартала года St = S 1=…
- –4
- –1/4
- 1/4
- 4
- Пусть Xt – значения временного ряда с квартальными наблюдениями, St – аддитивная сезонная компонента, причём для второго квартала года St = S 2=1, для третьего квартала года St = S 3=5, для четвёртого квартала года St = S 4=–8. Определите оценку сезонной компоненты для первого квартала года St = S 1=…
- –2
- 2
-
-
422. Пусть Xt – значения временного ряда с ежеквартальными наблюдениями, St – мультипликативная сезонная компонента, причём для первого квартала года St = S 1=1, для второго квартала года St = S 2=4, для четвёртого квартала года 
. Определите оценку сезонной компоненты для третьего квартала года St = S 3=…
- 0
-
-
-
- Пусть Xt – значения временного ряда с квартальными наблюдениями, St – аддитивная сезонная компонента, причём для второго квартала года St = S 2=1, для третьего квартала года St = S 3=–2, для четвёртого квартала года St = S 4=4. Определите оценку сезонной компоненты для первого квартала года St = S 1=…
- –3
- 0
- –5
- 3
424. Пусть Xt – значения временного ряда с квартальными наблюдениями, St – мультипликативная сезонная компонента, причём для первого квартала года St = S 1=2, для второго квартала года 
, для третьего квартала года St = S 3=2. Определите оценку сезонной компоненты для четвёртого квартала года St = S 4=…
- 1/3
- 3
- –19/4
- 19/4
425. Пусть Xt – значения временного ряда с квартальными наблюдениями, St – аддитивная сезонная компонента, причём для первого квартала года St = S 1=1, для второго квартала года St = S 2=6, для четвёртого квартала года St = S 4=–10. Определите оценку сезонной компоненты для третьего квартала года St = S 3=…
- 3
- –3
- 9
- –7
426. Пусть для временного ряда Xt было получено аналитическое выражение TCt для тренд-циклической компоненты и значения аддитивной сезонной компоненты St. Тогда прогнозное значение 
будет находиться по правилу …
-
-
-
-
- Пусть Xt – значения временного ряда, TCt – тренд-циклическая компонента этого ряда, St – сезонная компонента, Et – случайная компонента. Тогда общий вид мультипликативной модели временного ряда можно представить как …
- Xt = TCt + St + Et
- Xt = TCt · St · Et
- Xt = TCt + St · Et
- Xt = TCt · St + Et
- Пусть Xt – значения временного ряда, TCt – тренд-циклическая компонента этого ряда, St – сезонная компонента, Et – случайная компонента,
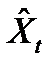– выровненный методом скользящей средней исходный ряд. При выделении аддитивной сезонной компоненты в качестве отличия сезонного явления от тренд-циклической составляющей используется … -
-
-
-
429. Способом включения случайного возмущения в регрессионную модель y = a + bx, при котором сохраняется линейная форма модели, является …
o мультиколлинеарный
o аддитивный
o экспоненциальный
o мультипликативный
430. Тенденция временного ряда описывается с помощью ____ компоненты.
- сезонной
- случайной
- трендовой
- фиктивной
Тема: Модели стационарных и нестационарных временных рядов и их идентификация
- Временной ряд называется слабо стационарным (стационарным в слабом смысле, стационарным в широком смысле), если независимо от рассматриваемого периода времени …
- его среднее значение и дисперсия имеют постоянное значение, а автоковариация зависит только от длины лага
- дисперсия зависит только от длины лага, а среднее значение и автоковариация постоянны
- среднее значение зависит только от длины лага, а дисперсия и автоковариация постоянны
- среднее значение, дисперсия, автоковариация постоянны
432. Временной ряд называется стационарным, если он является реализацией _______ процесса
- стационарного стохастического
- нестационарного стохастического
- функционального
- неслучайного
433. В эконометрической практике стационарность временного ряда означает …
o наличие тренда
o отсутствие систематических изменений дисперсии
o наличие строго периодических колебаний
o систематические изменения дисперсии
434. Для временного ряда рассматривается авторегрессионный процесс 1-го порядка Yt = α 0+ α 1 Yt -1+ εt. Известно, что 
. Временной ряд является...
- рядом, имеющим постоянный тренд
- стационарным
- описанием взрывного процесса
- нестационарным
- Единовременное шоковое воздействие на временные ряды имеет большую инерцию. Показатели долгое время остаются на новом уровне, не возвращаясь к своему прежнему положению. Речь идёт о …
o нестационарных рядах
o рядах типа «белый шум»
o рядах с постоянным долгосрочным средним значением
o стационарных рядах
436. Если случайные величины, образующие «белый шум» распределены нормально, тогда...
- временной ряд имеет тренд
- для временного ряда ярко выражены сезонные колебания
- этот временной ряд называется гауссовским белым шумом
- временной ряд является нестационарным
437. Модель временного ряда, имеющая следующую спецификацию Yi = Ti · Si + Ci + Ei (где Yi – уровень временного ряда, Ti – тренд, Si – сезонная компонента, Ci – конъюнктурная компонента, Ei – случайная компонента), называется …
o аддитивной
o нелинейной
o мультипликативной
o смешанной
438. Под стационарным процессом можно понимать …
- функциональный процесс
- процесс с возрастающей тенденцией
- процесс с убывающей тенденцией
- стохастический процесс, для которого среднее и дисперсия независимо от рассматриваемого периода имеют постоянное значение
439. При моделировании временных рядов экономических показателей необходимо учитывать характер уровней исследуемых показателей …
- конструктивный
- не зависящий от времени
- стохастический
- аналитический
440. Стационарность временного ряда означает отсутствие …
o тренда
o наблюдений по уровням временного ряда
o значений уровней ряда
o временной характеристики
441. Стационарность характерна для временного ряда …
- типа «белый шум»
- с положительной динамикой роста
- содержащего сезонные колебания
- с отрицательной динамикой роста
442. Стохастическим процессом называется …
- набор случайных переменных X (t), где t – вещественные числа
- набор неслучайных переменных X (t), где t – вещественные числа
- функциональная связь X (t), где t – вещественные числа
- набор случайных переменных X (t), где t – иррациональные числа
443. Эргодичность временного ряда позволяет...
- анализировать свойства остатков временного ряда
- выделять сезонные колебания временного ряда
- использовать выборочные аналоги генеральных характеристик временного ряда для определения его свойств
- использовать метод наименьших квадратов для аналитической записи тренда
Тема: Общие понятия о системах уравнений, используемых в эконометрике
444. В систему одновременных уравнений входят алгебраические соотношения между эндогенными переменными. В них отсутствует случайная составляющая, нет параметров, подлежащих оценке. Эти соотношения являются …
o регрессионными уравнениями
o структурными соотношениями
o тождествами
o приведёнными формулами
445. Для моделирования сложных экономических систем целесообразно использовать …
o временной ряд
o систему эконометрических уравнений
o изолированное уравнение регрессии
o стационарный процесс
446. Для системы независимых уравнений матрица параметров при эндогенных переменных имеет ________ структуру.
o кососимметрическую
o треугольную
o диагональную
o общего вида, несимметрическую
447. Изолированное уравнение множественной регрессии может быть использовано для моделирования взаимосвязи экономических показателей, если …
- система не предполагает использование уравнений множественной регрессии
- факторы не взаимодействуют друг с другом
- при изменении переменной влечёт за собой изменения во всей системе взаимосвязанных признаков
- при изменении одного экономического показателя другие факторы также изменяются
- Левая часть системы взаимозависимых уравнений представлена вектором …
o независимых переменных
o зависимых переменных и случайных величин
o зависимых и независимых переменных
o зависимых переменных
449. Относительно системы 
верно следующее утверждение …
- система неидентифицируема
- система сверхидентифицируема
- система идентифицируема
- вопрос об идентификации системы не может быть решён
450. Переменные, задаваемые «извне», автономно от модели, называются …
o экзогенными
o эндогенными
o лаговыми
o структурными
451. Поведенческим уравнением системы эконометрических уравнений называется уравнение, которое …
o описывает модель взаимодействия между переменными, т.е. содержит подлежащие оценке параметры и случайные составляющие
o описывает модель взаимодействия между случайными составляющими, т.е. содержит только случайные составляющие
o описывает соотношение, выполняемое во всех случаях, т.е. не содержит подлежащие оценке параметры и случайные составляющие
o описывает ограничения на значения эндогенных и экзогенных переменных
452. При изучении взаимодействия спроса и предложения целесообразно использовать …
o уравнение зависимости спроса от цены
o уравнение зависимости предложения от цены
o изолированные уравнения
o систему эконометрических уравнений
- Применение традиционного МНК к структурной форме системы одновременных уравнений приводит к получению _________ оценок структурных параметров.
o несмещённых и несостоятельных
o несмещённых и состоятельных
o смещённых и несостоятельных
o смещённых и состоятельных
454. При построении системы эконометрических уравнений необходимо учитывать …
- среднюю величину каждой зависимой переменной
- значения наблюдений
- структуру связей реальной экономической системы
- максимальную величину каждого фактора
455. Система взаимозависимых уравнений в её классическом виде называется также системой __________ уравнений.
o изолированных
o одновременных
o рекурсивных
o независимых
- Система, в которой одни и те же эндогенные переменные входят в левую часть одних уравнений и в правую часть других уравнений, называется системой _________ уравнений.
o несовместных
o взаимосвязанных
o рекурсивных
o независимых
457. Система уравнений, в котором каждая эндогенная переменная рассматривается как функция только предопределённых переменных, называется системой ______ уравнений.
o независимых
o рекурсивных
o регрессионных
o одновременных
458. Система эконометрических уравнений включает в себя следующие переменные:
- зависимые
- комплексные
- предопределенные
- экономические
459. Система эконометрических уравнений предполагает наличие …
- нескольких зависимых и одного независимого признаков
- одного зависимого и совокупности независимых признаков
- нескольких зависимых и нескольких независимых признаков
- одного зависимого и нескольких независимых признаков
460. Укажите преимущества использования системы эконометрических уравнений перед изолированными уравнениями регрессии:
- для оценки параметров системы эконометрических уравнений всегда используется метод наименьших квадратов
- оценки параметров системы эконометрических уравнений всегда определяются одним значением
- экономическая система моделируется не одним, а несколькими уравнениями
- учитывается факт, что изменение одной переменной, как правило, не может происходить при абсолютной неизменности других
- Укажите справедливые утверждения по поводу системы эконометрических уравнений:
- содержит только лаговые и текущие экзогенные переменные
- включает множество эндогенных и множество экзогенных переменных
- предназначена для расчёта доверительных интервалов для коэффициентов регрессии
- система уравнений, каждое из которых может содержать эндогенные переменные других уравнений
Тема: Классификация систем эконометрических уравнений
- В системе независимых уравнений каждое уравнение представлено …
- совместным уравнением регрессии
- изолированным уравнением регрессии
- уравнением временного ряда
- рекурсивным уравнением регрессии
463. В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как …
- сумма количества зависимых переменных предыдущих уравнений и количества независимых факторов
- сумма количества зависимых переменных последующих уравнений и количества независимых факторов
- разность количества зависимых переменных предыдущих уравнений и количества независимых факторов
- разность количества зависимых переменных последующих уравнений и количества независимых факторов
464. Выделяют три класса систем эконометрических уравнений: …
- системы независимых уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений
- система независимых уравнений, системы изолированных уравнений и системы рекурсивных уравнений
- системы взаимозависимых уравнения, системы рекурсивных уравнений и системы возвратных уравнений
- системы одновременных уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений
- Для оценки параметров структурной модели системы необходимо, чтобы …
- все уравнения системы были неидентифицируемы или сверхидентифицируемы
- хотя бы одно уравнение системы было идентифицируемо или сверхидентифицируемо
- все уравнения системы были идентифицируемы или сверхидентифицируемы
- хотя бы одно уравнение системы было неидентифицируемо или сверхидентифицируемо
- Для системы независимых уравнений матрица параметров при эндогенных переменных имеет ______ структуру.
- диагональную
- общего вида, несимметричную
- кососимметрическую
- треугольную
467. Пусть D – число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, а H – число эндогенных переменных в уравнении. Имеется следующая макроэкономическая модель: 
где Ct – потребление в период t; It – инвестиции в период t; Gt –государственные расходы в период t; Yt – валовой национальный продукт в период t; Yt –1 – валовой национальный продукт в период t –1; 
, 
– ошибки уравнений. Определите для второго уравнения системы число D – H …
- 2
- 1
- 3
- 0
- Система уравнений, в которых каждая эндогенная переменная рассматривается как функция только предопределенных переменных, называется системой _____ уравнений.
- регрессионных
- независимых
- одновременных
- рекурсивных
469. Система уравнений считается неидентифицируемой, если …
- хотя бы одно уравнение системы является неидентифицируемым
- хотя бы одно уравнение системы является сверхидентифицируемым
- хотя бы одно уравнение системы является сверхидентифицируемым или неидентифицируемым
- чтобы все уравнения системы являются идентифицируемыми или сверхидентифицируемы
470. Система взаимозависимых уравнений в её классическом виде называется также системой _______ уравнений
- изолированных
- рекурсивных
- одновременных
- независимых
471. Системы эконометрических уравнений классифицируются по …
- количеству уравнений в системе
- количеству факторов в каждом уравнении системы
- способу ранжирования факторов в зависимости от силы влияния на моделируемые показатели
- способу вхождения зависимых и независимых переменных в уравнения регрессии
472. Структурные коэффициенты системы одновременных уравнений определяются однозначно по коэффициентам приведённой формы системы. Такая модель называется …
o неидентифицируемой
o идентифицируемой
o сверхидентифицируемой
o неопределённой
Тема: Условия идентифицируемости системы одновременных уравнений
- Выберите верные утверждения по поводу приведённой формы системы эконометрических уравнений:
- оценки параметров уравнений приведённой формы системы определяются только традиционным методом наименьших квадратов
- получается в результате преобразования структурной формы модели
- оценки параметров уравнений определяются только обобщённым методом наименьших квадратов
- система независимых уравнений
- Выберите верные утверждения по поводу экзогенных переменных:
- предопределённые переменные
- значения экзогенных переменных определяются вне модели
- зависимые переменные
- число экзогенных переменных системы равно числу эндогенных переменных системы
- Выберите верные утверждения по поводу эндогенных переменных:
- число эндогенных переменных равно числу экзогенных переменных
- значения эндогенных переменных определяются внутри модели
- предопределённые переменные
- зависимые переменные
476. Для оценки параметров структурной модели системы необходимо, чтобы …
o хотя бы одно уравнение системы было идентифицируемо или сверхидентифицируемо
o все уравнения системы были неидентифицируемы или сверхидентифицируемы
o хотя бы одно уравнение системы было неидентифицируемо или сверхидентифицируемо
o все уравнения системы были идентифицируемо или сверхидентифицируемо
477. Модель идентифицируема, если число параметров структурной формы модели …
- равно числу уравнений модели
- равно числу параметров приведённой формы модели
- больше числа параметров приведённой формы модели
- меньше числа параметров приведённой формы модели
478. Неидентифицируемость системы эконометрических уравнений устраняется …
o введением экзогенных переменных в соответствии с экономическим смыслом решаемой задачи
o увеличением числа наблюдений для каждой переменной
o введением дополнительных эндогенных переменных
o переходом к безразмерным переменным
479. Необходимым условием идентифицируемости уравнения является условие: число исключенных из уравнения предопределенных переменных не должно быть...
- меньше числа включённых эндогенных переменных
- меньше числа эндогенных переменных минус единица
- равно числу эндогенных переменных
- меньше числа включённых эндогенных переменных минус единица
480. Переменные, задаваемые «извне», автономно от модели, называются …
- экзогенными
- эндогенными
- лаговыми
- структурными
481. Поведенческим уравнением системы эконометрических уравнений называется уравнение, которое …
- описывает модель взаимодействия между переменными, т.е. содержит подлежащие оценке параметры и случайные составляющие
- описывает соотношение, выполняемое во всех случаях, т.е. не содержит подлежащие оценке параметры и случайные составляющие
- описывает модель взаимодействия между случайными составляющими, т.е. содержит только случайные составляющие
- описывает ограничения на значения эндогенных и экзогенных переменных
482. Под идентификационной моделью подразумевается …
- единственность соответствия между приведённой и структурной формами модели
- адекватность модели
- существование нескольких приведённых моделей для одной структурной формы
- достоверность модели
- Приведённая форма системы эконометрических уравнений – это модель системы эконометрических уравнений…
- в которой все переменные распределены по нормальному закону
- в которой в каждом из уравнений зависимой является эндогенная переменная, а независимыми – только экзогенные
- с треугольной матрицей коэффициентов
- служащая для определения коэффициентов парной корреляции
484. Структурной формой модели называется система _______ уравнений
- изолированных
- рекурсивных
- взаимосвязанных
- независимых
485. Структурные коэффициенты системы одновременных уравнений определяются однозначно по коэффициентам приведённой формы системы. Такая модель называется...
- идентифицируемой
- сверхидентифицируемой
- неидентифицируемой
- неопределённой
- Тождества, используемые в системе одновременных уравнений...
- не требуют ни проверки на идентификацию, ни оценки параметров в них
- не требуют ни проверки на идентификацию, но при этом оценка параметров нужна
- требуют проверки на идентификацию, но при этом оценка параметров не нужна
- требуют проверки на идентификацию, и оценки параметров
487. Уравнение системы считается идентифицируемым в соответствии с достаточным условием идентифицируемости, если …
o определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в данном уравнении, но присутствующих в системе, отличен от 0, а ранг этой матрицы не меньше числа эндогенных переменных в системе без одной
o число предопределённых переменных, отсутствующих в данном уравнении, но присутствующих в системе, равно числу экзогенных переменных в данном уравнении без одной
o число предопределённых переменных, отсутствующих в данном уравнении, но присутствующих в системе, равно числу эндогенных переменных в данном уравнении без одной
o определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в данном уравнении, но присутствующих в системе, отличен от 0, а ранг этой матрицы не меньше числа эндогенных переменных в данном уравнении без одной
488. Число приведённых коэффициентов системы одновременных уравнений больше числа структурных коэффициентов. Тогда модель является …
o независимой
o неидентифицируемой
o сверхидентифицируемой
o идентифицируемой
489. Экзогенными переменными не являются …
- независимые переменные
- зависимые переменные
- переменные х в уравнениях системы вида у=f (x)
- переменные, значение которых определяется вне системы
490. Эндогенными переменными в системе одновременных уравнений являются...
- зависимые переменные, определяемые данной системой
- фиктивные переменные
- лаговые экзогенные переменные
- переменные, определяемые внешними факторами
491. Эндогенными переменными не являются …
- переменные y в уравнениях системы вида у=f (x)
- зависимые переменные
- переменные, значение которые определяется внутри системы
- независимые переменные
Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов и двухшаговый метод наименьших квадратов
492. Двухшаговый МНК определения оценок структурных параметров используется в случае …
o неидентифицируемости хотя бы одного уравнения в системе
o отсутствия в системе тождеств
o использования в системе фиктивных переменных
o точной идентифицируемости системы одновременных уравнений или сверхидентифицируемости этой системы
493. Двухшаговый МНК предполагает ______ использование обычного МНК.
- двукратное
- однократное
- трёхкратное
- не использовать обычный МНК
494. Двухшаговый МНК применим для решения системы одновременных уравнений …
o только идентифицируемой
o только неидентифицируемой
o в качестве наиболее общего метода решения
o только сверхидентифицируемой
495. Для оценки коэффициентов структурной формы модели не применяют _____ метод наименьших квадратов
- косвенный
- трёхшаговый
- двухшаговый
- обычный
496. Для сверхидентифицируемой структурной формы системы одновременных уравнений при оценке параметров применяется ______ метод наименьших квадратов.
- двухшаговый
- традиционный
- косвенный
- трёхшаговый
497. Для точно идентифицируемой структурной формы системы одновременных уравнений при оценке параметров применяется ______ метод наименьших квадратов.
- трёхшаговый
- традиционный
- косвенный
- двухшаговый
498. Косвенный метод наименьших квадратов требует …
- преобразования структурной формы модели в приведённую
- линеаризации уравнений структурной формы модели
- линеаризации уравнений приведённой формы
- нормализации уравнений структурной формы
- Метод инструментальных переменных в двухшаговом МНК используется в случае …
o неидентифицируемой системы уравнений
o недостаточного числа экзогенных переменных
o сверхидентифицируемой системы уравнений
o точно идентифицируемой системы уравнений
500. Метод, суть которого состоит в использовании в качестве инструментальной переменной теоретической оценки переопределённой переменной, полученной на базе экзогенных (или предопределённых) переменных модели, является …
- двухшаговым методом наименьших квадратов (ДМНК)
- обобщённым методом наименьших квадратов (ОМНК)
- косвенным методом наименьших квадратов (КМНК)
- обычным методом наименьших квадратов (МНК)
501. Метод, суть которого состоит в нахождении структурных коэффициентов модели через приведённые, оценённые обычным МНК, называется …
- косвенным методом наименьших квадратов (КМНК)
- обобщённым методом наименьших квадратов (ОМНК)
- двухшаговым методом наименьших квадратов (ДМНК)
- обычным методом наименьших квадратов (МНК)
502. На первом этапе применения косвенного метода наименьших квадратов …
- проводят процедуру линеаризации приведённой формы модели
- приведённую форму преобразуют в структурную
- проводят процедуру линеаризации структурной формы модели
- структурную форму преобразуют в приведённую
- Неидентифицируемую модель в виде системы одновременных уравнений можно превратить в точно идентифицируемую...
- переходя от структурной к приведённой форме модели
- с помощью традиционного метода наименьших квадратов
- используя косвенный метод наименьших квадратов
- вводя дополнительные ограничения на структурные коэффициенты
- Оценки параметров неидентифицируемой системы эконометрических уравнений …
- не могут быть найдены обычным МНК
- могут быть найдены косвенным МНК
- могут быть найдены обычным МНК
- могут быть найдены двухшаговым МНК
- Оценки параметров сверхидентифицируемой системы эконометрических уравнений могут быть найдены с помощью …
- взвешенного МНК
- косвенного МНК
- обычного МНК
- двухшагового МНК
506. Первый шаг двухшагового метода наименьших квадратов состоит в нахождении теоретических значений...
- эндогенных переменных из приведённой формы модели традиционным методом наименьших квадратов
- экзогенных переменных из приведённой формы модели традиционным методом наименьших квадратов
- эндогенных переменных из приведённой формы модели косвенным методом наименьших квадратов
- экзогенных переменных из приведённой формы модели косвенным методом наименьших квадратов
507. Приведена последовательность операций:
1. к системе одновременных уравнений применяется обобщённый метод наименьших квадратов с целью устранения корреляции случайных отклонений
2. заданная система одновременных уравнений из структурной формы преобразуется в приведённую форму
3. оценки параметров приведённой формы находятся традиционным методом наименьших квадратов
4. определение расчётных значений эндогенных переменных, которые выступают в качестве факторов в структурной форме модели
5. определение структурных параметров каждого уравнения в отдельности традиционным методом наименьших квадратов, используя в качестве факторов входящие в это уравнение предопределённые переменные и расчетные значения эндогенных переменных, полученные на первом шаге.
Этот алгоритм соответствует _____ методу наименьших квадратов.
- трёхшаговому
- обобщённому
- косвенному
- традиционному
508. Приведённая форма модели является результатом преобразования …
- структурной формы модели
- системы независимых уравнений
- системы рекурсивных уравнений
- нелинейных уравнений регрессии
509. При оценке параметров приведённой формы модели косвенный метод наименьших квадратов использует алгоритм …
o обычного МНК
o расчёта средней взвешенной величины
o метода максимального правдоподобия
o метода главных компонент
510. С помощью традиционного метода наименьших квадратов можно определить параметры уравнений, входящих в систему _____ уравнений.
- одновременных или независимых
- только одновременных
- рекурсивных или одновременных
- независимых или рекурсивных
