o при увеличении моделируемых значений результативного признака значение остатка увеличивается
o при уменьшении моделируемых значений результативного признака значение остатка уменьшается
o остаточные величины имеют неслучайный характер
169. Причинами нарушения предпосылок МНК могут являться …
- наличие в уравнении фиктивных переменных
- нелинейный характер зависимости между переменными
- наличие неучтённого в уравнении существенного фактора
- большой объём наблюдений
170. Традиционный метод наименьших квадратов применяется для оценки параметров...
- классической линейной регрессионной модели
- линейной регрессионной модели с гетероскедастичностью в остатках
- линейной регрессионной модели с автокорреляцией в остатках
- нелинейной по параметрам регрессионной модели
171. Укажите выводы, которые соответствуют графику зависимости остатков e от теоретических значений зависимой переменной  :
:
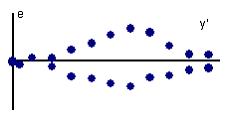
- модель содержит циклическую компоненту
- нарушена предпосылка МНК о постоянстве дисперсий случайных отклонений
- нарушена предпосылка МНК о равенстве нулю математического ожидания случайных отклонений
- имеет место гетероскедастичность остатков
- Эмпирический коэффициент b регрессии y = a + bx + ε является несмещённой оценкой теоретического коэффициента β регрессии y = α + βx + ε при условии, что …
o дисперсия оценки b является наименьшей среди всех возможных дисперсий несмещённых оценок параметра β
o математическое ожидание оценки b равно 0
o математическое ожидание оценки b равно оцениваемому параметру β
o дисперсия оценки b равна 0
Тема: Обобщённый метод наименьших квадратов
173. Для использования обобщённого МНК необходимо знать …
o автокорреляционную функцию
o коэффициент детерминации
o автоковариационную матрицу случайных возмущений
o значение критерия Фишера
174. Для регрессионной модели Yi = b 0+ b 1 X 1 i + b 2 X 2 i +…+ bmXmi + εi, i =1… n, с гетероскедастичностью остатков при отсутствии автокорреляции остатков ковариационная матрица возмущений является...
- диагональной
- единичной
- треугольной
- вырожденной
- К методам устранения автокорреляции остатков не относятся:
- метод Голдфелда–Квандта
- обобщённый метод наименьших квадратов
- метод Кохрана–Оркатта
- традиционный метод наименьших квадратов
176. Метод оценки параметров моделей с гетероскедастичными остатками называется … методом наименьших квадратов
- минимальным
- обычным
- косвенным
- обобщённым
177. Множественная линейная регрессионная модель, в которой не выполняются условия гомоскедастичности и (или) имеет место автокорреляция остатков, называется ______ регрессионной моделью.
- обобщённой линейной
- нелинейной
- парной
- множественной линейной
178. На основании преобразования переменных при помощи обобщённого метода наименьших квадратов получаем новое уравнение регрессии, которое представляет собой …
- нелинейную регрессию, в которой переменные взяты с весами
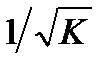
- нелинейную регрессию, в которой переменные взяты с весами

- взвешенную регрессию, в которой переменные взяты с весами

- взвешенную регрессию, в которой переменные взяты с весами

179. Обобщённый МНК для регрессионной модели с гетероскедастичностью, когда известны диагональные элементы автоковариационной матрицы случайных возмущений, называется ____________ методом наименьших квадратов.
o косвенным
o взвешенным
o доступным обобщённым
o двухшаговым
180. Обобщённый МНК используется для линейных уравнений регрессии с ________ остатками.
- нулевыми
- гетероскедастичными и/или автокоррелированными
- гомоскедастичными
- некоррелированными
- Обобщённый МНК может использоваться для корректировки _______ остатков.
- стандартной ошибки
- гетероскедастичности
- автокорреляции
- доверительного интервала
- Обобщённый МНК может применяться в случае нарушения предпосылки МНК о(об) _______ остатков.
- существовании
- отсутствии автокорреляции
- гомоскедастичности
- максимизации суммы квадратов
183. Обобщённый МНК рекомендуется применять в случае …
- автокорреляции остатков
- гомоскедастичных остатков
- нормально распределённых остатков
- автокорреляции результативного признака
184. Обобщённый МНК отличается от обычного МНК тем, что при применении ОМНК …
- остатки не изменяются
- остатки приравниваются к нулю
- преобразуются исходные уровни переменных
- уменьшается количество наблюдений
185. После применения обобщённого МНК удаётся избежать ______ остатков
- гетероскедастичности
- случайного характера
- равенства нулю суммы
- нормального распределения
186. Проявление гетероскедастичности в остатках удаётся устранить при помощи метода обобщённого метода наименьших квадратов путём …
- преобразования переменных
- расчёта критерия Дарбина–Уотсона гомоскедастичных остатков
- введения в модель фиктивных переменных
- введения в выражение для дисперсии остатков коэффициента пропорциональности
- Теоретическое распределение случайной составляющей регрессионной модели является различным для разных наблюдений в выборке. Тогда имеет место неодинаковый разброс случайных составляющих или __________ остатков.
o гомоскедастичность
o детерминированность
o гетероскедастичность
o автокорреляция
- Что преобразуется при применении обобщённого МНК?
o коэффициент корреляции
o дисперсия результативного признака
o дисперсия факторного признака
o исходные уровни переменных
Тема: Оценка качества подбора уравнения
- G 2(Y)= σ 2(Y)+ δ 2(Y), где G 2(Y) – общая дисперсия зависимой переменной, σ 2(Y) – дисперсия, объяснённая построенным уравнением регрессии, δ 2(Y) – дисперсия, не объяснённая построенным уравнением регрессии. Сформулированное утверждение является...
- теоремой о разложении дисперсии
- формулировкой теоремы Гаусса–Маркова
- исходным соотношением, используемым в методе наименьших квадратов
- F -критерием Фишера
190. В качестве показателя тесноты связи для линейного уравнения парной регрессии используется




