Передаточное отношение:
Условие соосности:
Z1+Z2=Z4-Z3; 37+37=111-37; 74=74
Условие соседства:
где Z=Z2=37 – большее из колес сателлитного блока,
Условие сборки:
где p=2,0 – число дополнительных полных оборотов водила при монтаже механизма;
с – произвольное целое число.
Условие отсутствия заклинивания для пары внешнего зацепления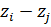 
;
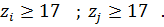
Для пары внутреннего зацепления:
Основные условия синтеза для выбранного варианта чисел зубьев выполняются.
Вычерчивание схемы механизма и диаграмм линейных и угловых скоростей
Радиусы начальных окружностей колес:
Окружная скорость точек колес z 1 и z2, совпадающих с полюсом зацепления P12:
На листе 1 графической части работы вычерчиваем схему планетарного механизма в масштабе 1:2 (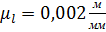
) и строим для него картину линейных скоростей при 
и план угловых скоростей при 
.
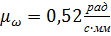Используя план угловых скоростей, определим частоты вращения и угловые скорости звеньев планетарного механизма и проверим графически его передаточное отношение:
n2=n3=(0-2,3) 
=69,747∙5=348,73 мин-1;
ω2=ω3=(0-2,3) 
= 69,747∙0,52=36,26 рад/с;
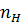=(0-H) 
= 34,936∙5=174,68 мин-1;
(0-H) = 34,936∙0,52=18,16 рад/с;
U1H = 
= 
= 
=4,0.
ДИНАМИЧЕСКИЙ СИНТЕЗ КУЛАЧКОВОГО МЕХАНИЗМА
(лист 2 графической части работы)
В данной работе необходимо выполнить синтез кулачкового механизма с поступательно движущимся плоским тарельчатым толкателем с силовым замыканием (рис.3.1)
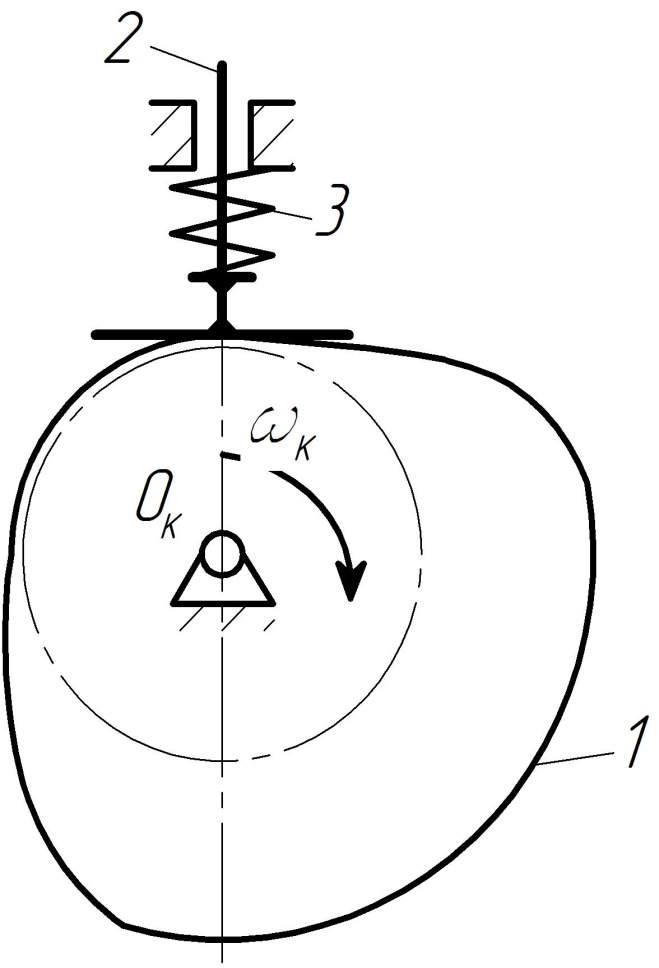
1-кулачок; 2-плоский толкатель; 3-пружина
Рисунок 3.1 – Схема кулачкового механизма
Задача синтеза кулачкового механизма состоит в построении профиля кулачка, обеспечивающего заданные законы движения толкателя.
Входные параметры синтеза
Входными параметрами синтеза кулачкового механизма являются:
- ход толкателя h=35 мм;
- фазовые углы:
· удаления jу=90 град;
· дальнего выстоя jдв=90º;
· приближения jпр=70 º;
- законы движения толкателя:
· на фазе удаления - косинусоидальный;
· на фазе приближения – синусоидальный.
Поскольку полный рабочий цикл механизма совершается за один оборот кулачка, определим фазовый угол ближнего выстоя:
Переведем фазовые углы в радианную меру. Для этого воспользуемся формулой:
.
3.2 Расчет и построение диаграмм движения толкателя
Для построения профиля кулачка необходимо иметь зависимость перемещения толкателя от угла поворота кулачка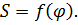 
Закон движения толкателя в задании представлен в виде зависимости аналога ускорения толкателя от угла поворота кулачка 
Для нахождения искомой зависимости 
необходимо дважды проинтегрировать функцию 
. Построим на втором листе работы указанную зависимость и дважды графически проинтегрируем её, предварительно рассчитав экстремальные значения аналогов скоростей и ускорений на фазах удаления и приближения.
На фазе удаления:
аналог ускорения
аналог скорости
На фазе приближения:
аналог ускорения
аналог скорости
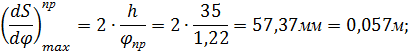
где h=35 мм – ход толкателя;
фазовые углы, рад.
Используя полученные максимальные значения аналогов скоростей и ускорений, вычерчиваем диаграммы движения толкателя
при следующих масштабных коэффициентах:
для аналогов ускорений 
для аналогов скоростей 
для перемещений 
для углов поворота кулачка 
Определим длины отрезков, изображающих фазовые углы:
Проверим:
