Карточки-тренажеры
Карточки-тренажеры можно использовать как обучающие, ликвидации пробелов знаний по теме «Обыкновенные дроби».
Сравнение, сложение и вычитание дробей с одинаковыми знаменателями.
| Указание | Образец | Задания |
| Сравнивай, складывай, вычитай числители. |
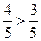 , так как
4 > 3. , так как
4 > 3.
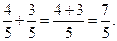
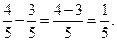
|
Сравнить числа, найти их сумму и разность:
1) 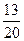 и и 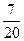 ; 2) ; 2) 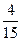 и и 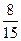 ; 3) ; 3) 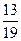 и и 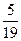 ;
4) ;
4) 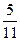 и и 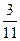 ; 5) ; 5) 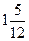 и и 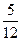 ; 6) ; 6) 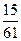 и и 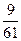 ;
7) ;
7) 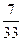 и и 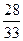 ; 8) ; 8) 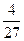 и и 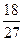 ; 9) ; 9) 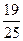 и и 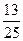 ;
10) ;
10) 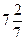 и и 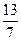 ; 11) ; 11) 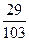 и и 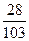 ; 12) ; 12) 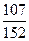 и и 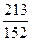 ;
13) ;
13) 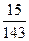 и и 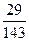 ; 14) ; 14) 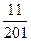 и и 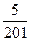 ; 15) ; 15) 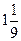 и и 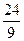 . .
|
Основное свойство дроби.
| Правило | Образец | Задания |
| Приведение дроби к новому знаменателю: 1.Умножь (или раздели) знаменатель дроби на число. 2.Умножь (или раздели) числитель дроби на то же число. 3.Запиши в ответе получившуюся дробь. |
Привести дробь 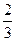 к знаменателю 15.
Решение.
1) 3 × 5 = 15;
2) 2 × 5 = 10;
3) Ответ: к знаменателю 15.
Решение.
1) 3 × 5 = 15;
2) 2 × 5 = 10;
3) Ответ: 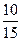 .
Привести дробь .
Привести дробь 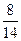 к знаменателю 7.
Решение.
1) 14: 2 = 7;
2) 8: 2 = 4;
3) Ответ: к знаменателю 7.
Решение.
1) 14: 2 = 7;
2) 8: 2 = 4;
3) Ответ: 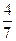 . .
|
Привести дроби
к знаменателю 24:
1) 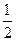 ; 6) ; 6) 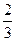 ; 11) ; 11) 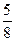 .
Привести дроби к знаменателю 7:
2) .
Привести дроби к знаменателю 7:
2) 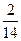 ; 7) ; 7) 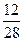 ; 12) ; 12) 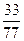 .
Разделить числитель и знаменатель дроби на 2:
3) .
Разделить числитель и знаменатель дроби на 2:
3) 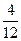 ; 8) ; 8) 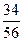 ; 13) ; 13) 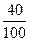 .
Умножить числитель и знаменатель дроби на 2:
4) .
Умножить числитель и знаменатель дроби на 2:
4) 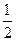 ; 9) ; 9) 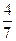 ; 14) ; 14) 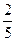 ;
Разделить числитель и знаменатель дроби на возможно большее число:
5) ;
Разделить числитель и знаменатель дроби на возможно большее число:
5) 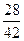 ; 10) ; 10) 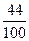 ; 15) ; 15) 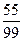 . .
|
Сравнение, сложение и вычитание дробей с разными знаменателями.
| Правило | Образец | Задания |
| 1) Привести дроби к наименьшему общему знаменателю. 2) Сравнить, сложить или вычесть получившиеся дроби с одинаковыми знаменателями. | Сравнить 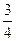 и и 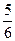 , найти их сумму и разность.
Решение.
1) , найти их сумму и разность.
Решение.
1) 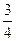 = = 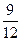 , , 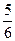 = = 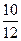 ;
2) 9 < 10, значит, ;
2) 9 < 10, значит, 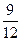 < < 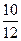 , то есть , то есть
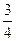 < < 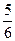 ; ;
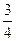 + + 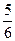 = = 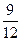 + + 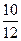 = = 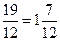 . .
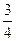 – – 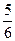 = = 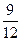 – – 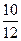 = = 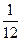 . .
| Сравнить дроби, найти их сумму и разность:
1) 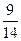 и и 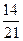 ; 9) ; 9) 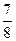 и и 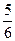 ;
2) ;
2) 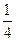 и и 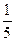 ; 10) ; 10) 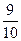 и и 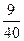 ;
3) ;
3) 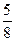 и и 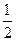 ; 11) ; 11) 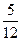 и и 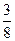 ;
4) ;
4) 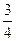 и и 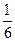 ; 12) ; 12) 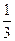 и и 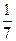 ;
5) ;
5) 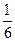 и и 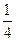 ; 13) ; 13) 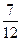 и и 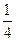 ;
6) ;
6) 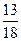 и и 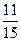 ; 14) ; 14) 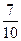 и и 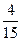 ; ;
|
Умножение дробей.
| Правило | Образец | Задания |
Умножь числитель на числитель и знаменатель на знаменатель:
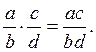
|
1) 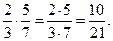 2)
2) 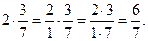 3)
3) 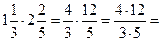 =
= 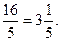
|
Найдите произведение дробей:
1) 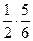 ; 2) ; 2) 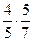 ;
3) ;
3) 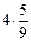 ; 4) ; 4) 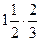 ;
5) ;
5) 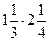 ; 6) ; 6) 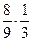 ;
7) ;
7) 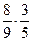 ; 8) ; 8) 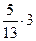 ;
9) ;
9) 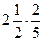 ; 10) ; 10) 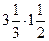 ; ;
|
Деление дробей.
| Правило | Образец | Задания |
Умножь числитель на знаменатель и знаменатель на числитель:
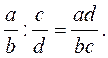
|
1) 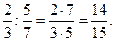 2)
2) 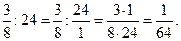 3)
3) 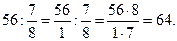 4)
4) 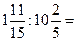 =
= 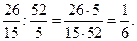 5)
5) 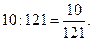
|
Найдите частное дробей:
1) 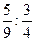 ; 2) ; 2) 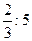 ; 3) ; 3) 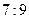 ; 4) ; 4) 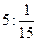 ; 5) ; 5) 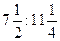 ; 6) ; 6) 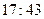 ;
7) ;
7) 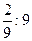 ; 8) ; 8) 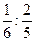 ; 9) ; 9) 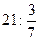 ; 10) ; 10) 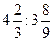 ; 11) ; 11) 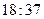 ; 12) ; 12) 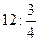 ;
13) ;
13) 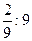 ; 14) ; 14) 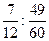 . .
|
Основное свойство пропорции.
| Правило | Образец | Задания |
| Произведение крайних членов пропорции равно произведению ее средних членов. Неизвестный крайний член пропорции равен произведению ее средних членов, деленному на известный крайний. Неизвестный средний член пропорции равен произведению ее крайних членов, деленному на известный средний. | Проверить пропорцию 0,9: 3 = 0,3: 1. Решение: 0,9 × 1 = 0,9, 3 × 0,3 = 0,9. Решить уравнение: а) х: 7 = 18: 14; б) 25: 75 = 2: х. Решение: а) х = 7 × 18: 14 = 9; б) х = 75 × 2: 25 = 6. Решить уравнение: а) 24: х = 8: 13; б) 6: 2 = х: 70. Решение: а) х = 24 × 13: 8 = 39; б) х = 6 × 70: 2 = 210. | 1) Проверить пропорцию:
1: 2 = 0,2: 0,4.
Решить уравнения:
2) х: 7 = 9: 2;
3) 5: 3 = t: 6;
4) 1: 3 = x: 18;
5) 5: 4 = 25: y.
6) Проверить пропорцию
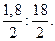 Решить уравнения:
7)
Решить уравнения:
7) 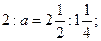 8)
8) 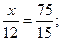 9)
9) 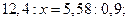 ;
10) ;
10) 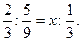 ;
11) Проверить пропорцию: ;
11) Проверить пропорцию:
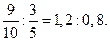 Решить уравнения:
12)
Решить уравнения:
12) 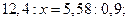 ;
13) ;
13) 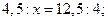 ;
14) ;
14) 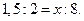
|
Смешанные числа.
| Правило | Образец | Задания | |||||
Дробь называется правильной, если знаменатель больше числителя.
Дробь называется неправильной, если знаменатель меньше числителя.
Чтобы неправильную дробь представить в виде смешанного числа, нужно числитель разделить на знаменатель.
Чтобы смешанное число представить в виде неправильной дроби нужно:
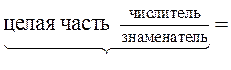 смешанное число
смешанное число
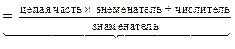 неправильная дробь
неправильная дробь
| 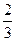 – правильная дробь. – правильная дробь.
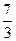 – неправильная дробь. – неправильная дробь.
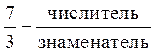 1) Выделить целую часть из дроби
1) Выделить целую часть из дроби 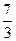 .
Решение: .
Решение:
2) Записать число Решение:
| Выделите целую часть числа:
1) 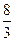 ; 2) ; 2) 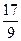 ;
3) ;
3) 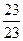 ; 4) ; 4) 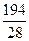 ;
5) ;
5) 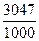 ; 6) ; 6) 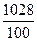 .
Представить в виде неправильной дроби:
7) .
Представить в виде неправильной дроби:
7) 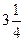 ; 8) ; 8) 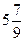 ;
9) ;
9) 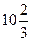 ; 10) ; 10) 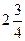 ; 11) ; 11) 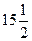 ; 12) ; 12) 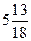 . .
|
Сложение и вычитание смешанных чисел.
| Правило | Образец | Задания |
| Чтобы сложить смешанные числа, нужно: 1) Сложить целые части; 2) Сложить дробные части; 3) Результаты сложить. Чтобы вычесть смешанные числа, нужно: 1) Вычесть целые части; 2) Вычесть дробные части, если числитель вычитаемого больше числителя уменьшаемого, то необходимо занять единицу от целой части уменьшаемого и выполнить вычитание; 3) Результаты сложить, если возможно сократить. | 1) Выполните действие: 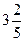 + + 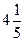 .
Решение: .
Решение:
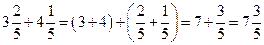 2) Выполните действие: а)
2) Выполните действие: а) 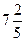 – – 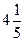 ;
б) ;
б) 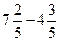 .
Решение:
а) .
Решение:
а) 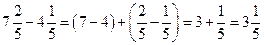 б)
б) 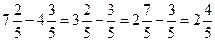 3) Вычисли:
3) Вычисли: 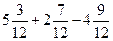 .
Решение: .
Решение:
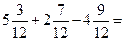 =
= 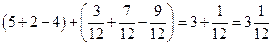
| Вычисли:
1) 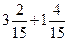 ;
2) ;
2) 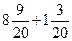 ;
3) ;
3) 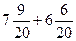 ;
4) ;
4) 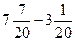 ;
5) ;
5) 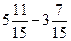 ;
6) ;
6) 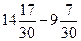 ;
7) ;
7) 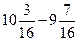 ;
8) ;
8) 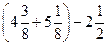 ;
9) ;
9) 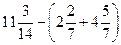 ;
10) ;
10) 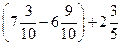 . .
|
| Правило | |||||
Дробь называется правильной, если знаменатель больше числителя.
Дробь называется неправильной, если знаменатель меньше числителя.
Чтобы неправильную дробь представить в виде смешанного числа, нужно числитель разделить на знаменатель.
Чтобы смешанное число представить в виде неправильной дроби нужно:
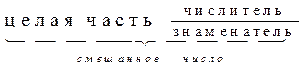 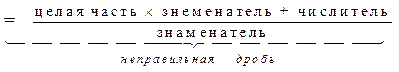
| |||||
| Образец | |||||
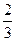 – правильная дробь. – правильная дробь.
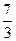 – неправильная дробь. – неправильная дробь.
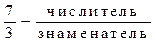 1) Выделить целую часть из дроби
1) Выделить целую часть из дроби 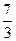 , это значит числитель 7 разделить на знаменатель 3.
Решение: , это значит числитель 7 разделить на знаменатель 3.
Решение:
2) Записать число Решение:
|





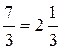
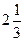 в виде неправильной дроби.
в виде неправильной дроби.