Mathcad позволяет вычислять кратные интегралы непосредственно, однако в большинстве случаев при кратности интегралов 3 и более применение самого метода Монте-Карло предпочтительнее. Дело в том, при одинаковой точности метод Монте-Карло дает существенный выигрыш во времени (в десятки и сотни раз), особенно при большой кратности интегралов. Идея метода состоит в том, что интеграл заменяется величиной Fср.·V, где V – объем области интегрирования, Fср. – среднее значение подынтегральной функции, вычисленное по нескольким случайно выбранным точкам.
Определим подынтегральную функцию.
И вычислим интеграл
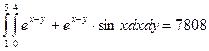
Тот же интеграл можно вычислить непосредственно методом Монте-Карло, а можно вычислить и другим способом. Заключим область интегрирования внутрь прямоугольной области, "набросаем" внутрь полученной области N случайных точек. Тогда интеграл найдем из соотношения 
,где N – общее число точек, n – число точек, лежащих внутри области интегрирования, V – объем области, включающей область интегрирования.
Вывод
Существует много задач, для решения которых случайный подход более эффективный, чем другие математические методы. Метод Монте-Карло применялся во многих задачах, однако его использование не всегда было оправдано из-за большого количества вычислений, необходимых для получения ответа с заданной точностью. Существует класс задач, сложность (количество вычислений, необходимых для получения точного ответа) которых растет с размерностью задачи экспоненциально. Иногда можно, пожертвовав точностью, найти алгоритм, сложность которого растет медленнее, но есть большое количество задач, для которого этого нельзя сделать и метод Монте-Карло является единственной возможностью для получения достаточно точного ответа за приемлемое время.
На примере интегралов видно, что необходимость применения численных методов, а именно метода Монте-Карло, чаще всего может быть вызвана отсутствием у первообразной функции представления в элементарных функциях и, следовательно, невозможностью аналитического вычисления значения определенного интеграла. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом. Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминистических методов. Тем не менее, в некоторых случаях, когда функция задана не явно, а необходимо определить область, заданную в виде сложных неравенств, случайный метод более предпочтительный
Я реализовал метод Монте-Карло в приложении BPW, а также в пакете Mathcad. Программная реализация метода показывает, что при увеличении количества генерирования случайных чисел возрастает время подсчета интеграла. Mathcad позволяет вычислять кратные интегралы непосредственно, однако в большинстве случаев при кратности интегралов 3 и более применение самого метода Монте-Карло предпочтительнее. Дело в том, при одинаковой точности метод Монте-Карло дает существенный выигрыш во времени (в десятки и сотни раз), особенно при большой кратности интегралов.
В настоящее время основные усилия исследователей направлены на создание эффективных Монте-Карло алгоритмов различных физических химических и социальных процессов для параллельных вычислительных систем.
Метод Монте-Карло используется очень часто, порой некритично и неэффективным образом. Он имеет некоторые очевидные преимущества:
а) Он не требует никаких предложений о регулярности, за исключением квадратичной интегрируемости. Это может быть полезным, так как часто очень сложная функция, чьи свойства регулярности трудно установить.
б) Он приводит к выполнимой процедуре даже в многомерном случае, когда численное интегрирование неприменимо, например, при числе измерений, больше 10.
в) Его легко применять при малых ограничениях или без предварительного анализа задачи.
Он обладает, однако, некоторыми недостатками, а именно:
а) Границы ошибки не определены точно, но включают некую случайность. Это, однако, более психологическая, чем реальная, трудность.
б) Статическая погрешность убывает медленно.
в) Необходимость иметь случайные числа.
Литература
1. Статья «Моделируя жизнь», автор Андрей Тепляков.
2. Статья «Metopolis, Monte Carlo and the MANIAC».
3. Статья о Монте-Карло на www.riskglossary.com
4. ISBN 5030033920 Д.Каханер, К.Моулер, С.Нэш. Численные методы и программное обеспечение (пер. с англ.). М.: Мир, 2001, 575 c.
5. Численные методы на Mathcad.
