Однорозрядні схеми суматорів

Найпростішим сумуючим елементом є чвертьсуматор. Найбільш відомі для даної схеми назви: елемент “сума по mod 2” і елемент “виключаюче АБО”.

Схема (рис. 1.1) має два входи 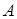і 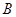для двох доданків і один вихід 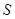для суми. Работу її відображає таблиця істинності (табл. 1.1), а відповідне рівняння має вигляд:

. (1.1)

а) б)

Рис. 1.1. Умовне графічне позначення чвертьсуматора (а) та еквівалентного йому елементу “виключаюче АБО” (б)

Табл. 1.1

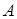
Даний елемент випускається у вигляді ІС типу ЛП5 (серій 133, 155, 530, 531, 533, 555, 1531, 1533); ЛП2 (561, 564); ЛП4 (1561) і т. д.

Реалізуємо чвертьсуматор в базисах І-НЕ і АБО-НЕ, для чого перетворимо рівняння (17.1):

, (1.2)

. (1.3)

(1.4)

(1.5)

Схеми, що реалізують логічні функції (1.2), (1.3), (1.4) і (1.5) приведені відповідно на рис. 1.2, рис. 1.3, рис. 1.4, рис. 1.5.

Рис. 1.2. Схема чвертьсуматора в базисі І-НЕ

Рис. 1.3. Схема чвертьсуматора в базисі АБО-НЕ

Рис. 1.4. Схема чвертьсуматора в базисі І-НЕ

Рис. 1.5. Схема чвертьсуматора в базисі АБО-НЕ

Напівсуматор (рис. 1.6) має два входи 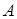і для двох доданків і два виходи: 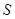- сума, - перенос. Для позначення напівсуматора використовують букви (half sum – напівсума). Роботу напівсуматора відображає таблиця істинності (табл. 1.2).

Табл. 1.2

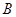
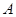
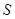
Згідно табл. 1.2 рівняння, що описує роботу напівсуматора має вигляд:

. (1.6)

Рис. 1.6. Функціональне позначення напівсуматора (а) та його реалізація на елементах “виключаюче АБО” і І (б).

З рівнянь (1.6) випливає, що для реалізації напівсуматора необхідно один елемент “виключаюче АБО” та один елемент 2І-НЕ (рис. 1.6а). На рис. 1.7а показана реалізація напівсуматора в базисі І-НЕ. В даній схемі один з логічних елементів використовується як інвертор, а всього операцій інвертування – п’ять. Реалізуємо напівсуматор з використанням тільки одного інвертора, для чого рівняння суми запишемо в вигляді:

(1.7)

Схема напівсуматора, що реалізує рівняння (1.7), приведена на рис. 1.7б.

Рис. 1.7. Напівсуматор в базисі І-НЕ (а), з одним інвертором (б).

Повний однорозрядний двійковий суматор (рис. 1.8) має три входи: - для двох доданків і - перенесення з попереднього (молодшого) розряду та два виходи: 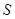- сума, - перенесення в наступний (старший) розряд. Повний двійковий суматор позначається буквами . Роботу суматора відображає таблиця істинності (табл. 1.3).

Рис. 1.8. Функціональне позначення повного двійкового однорозрядного суматора.

Табл. 1.3

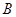
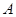
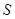
Рівняння, що описують роботу повного двійкового суматора, представлені ДДНФ, згідно табл. 1.3, мають вигляд:

. (1.8)

Використовуючи карти Карно (рис. 1.9а, б) мінімізуємо логічні функці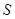ї і .

а) б)

Рис. 1.9. Карти Карно для суми 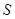а) і переносу б) повного однорозрядного суматора.

При стандартному підході рівняння для суми 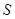не може бути мінімізовано (рис. 7.9а), а рівняння для переносу після мінімізації має вигляд:

. (1.9)

При практичному проектуванні суматора рівняння (1.8) можуть бути перетворені до вигляду, зручного для реалізації з допомогою заданих логічних елементів.

. (1.10)

З виразів (1.10) випливає, що повний двійковий суматор можна реалізувати з допомогою двох напівсуматорів та одного елемента 2АБО. Відповідна схема приведена на рис. 1. 10. Вираз для 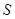також можна представити у вигляді:

. (1.11)

Рис.7.10. Повний двійковий суматор, реалізований на двох напівсуматорах

Розглянемо метод, який використовуються для отримання оптимальної схеми повного двійкового суматора, що є основою схем суматорів типу ІМ1(133, 155) та ін. Він базується на використанні значення вихідного перенесення як допоміжної змінної при визначенні вихідної суми 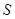(табл. 1.4). В табл. 1.4 при наборах змінних, що є нереальними (наприклад, одиничне значення переносу при нульових значеннях змінних 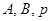, функція 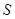приймає довільні значення довільним чином.

Табл. 1.4

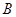
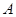
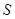
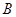
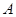
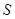
				X					X
									X
				X
									X
				X
				X					X

Карта Карно для суми 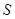представлена на рис. 1.11.

Рис.7.11. Карта Карно для суми 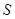(табл. 1.4).

З карти Карно для функції 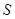після мінімізації отримуємо:

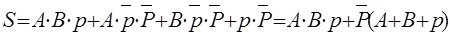(1.12)

Схема суматора, реалізованого згідно рівнянь (1.10) і (1.12), приведена на рис. 1.12а. В даній схемі використовуються багатовходові логічні елементи І та АБО. Якщо використовувати тільки двовходові елементи, то отримаємо схеми, зображені на рис. 1.12б і 1.12в.

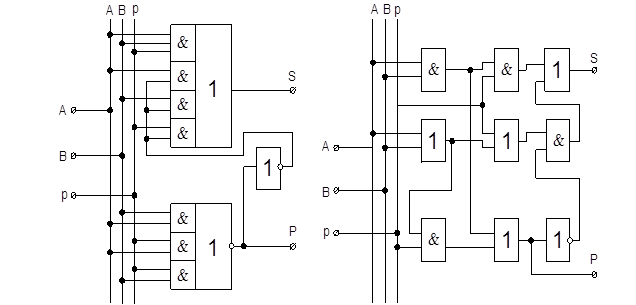
а) б)

в)

Рис. 1.12. Оптимальні схеми повного двійкового суматора: (а) – на багатовходових елементах; (б), (в) – на двовходових елементах.