Этот метод факторизации натурального числа N был разработан известным криптографом Джоном Поллардом и является самым быстрым среди простых методов факторизации. Его идея состоит в том, что порождается случайная последовательность чисел {xi} (например, взяв x0=2, и продолжить вычисление по формуле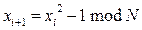 
). Далее, вычисляются всевозможные разности 
. Для каждой такой пары (xi, xj) находятся с помощью алгоритма Евклида наибольший общий делитель НОД(N, |xi - xj|)). Если будет найдена пара (xi, xj) со свойством НОД(N, |xi - xj|))>1, то этот НОД и даст искомый делитель числа N.
Обоснование метода Полларда. Пусть p –делитель N. Среди членов последовательности {xi} рано или поздно попадутся числа xi и xj такие, что 
= 
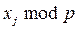(это равенство записывается более кратко 
). Это условие означает, что 
для некоторого целого числа k. Т.к. p – делитель N, то для выбранной пары (xi, xj) НОД(N; |xi - xj|)= p.
Оценка сходимости метода Полларда. Т.к. меньший делитель числа N меньше 
, то элементы последовательности 
меньше . По парадоксу близнецов (см. [1]) среди первых 
членов последовательности 
с вероятностью, большем чем 0,5, попадутся два одинаковых члена, т.е. найдутся i, j, удовлетворяющие условию . Поэтому, с вероятностью, большей 0,5, мы найдем искомый делитель N, просмотрев не более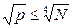 
, членов последовательности.
При практическом применении метода Полларда для сокращения объема вычисления рассматривают не все разности |xi - xj|, а только те, для которых номер j является степенью 2, т.е. принимает значения 2, 4, 8,...
Рассмотрим пример. Пусть N=1387. Зададим рекуррентную последовательность чисел {xi} следующим соотношением: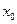 
=2, 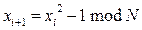. Значения строки xj определим равными ближайшему слева xi, у которого i является степенью 2 (такие xi выделены красным). В следующей строке поместим их разность, а в последней строке – НОД(N; |xi - xj|), вычисленный с помощью алгоритма Евклида.
| N | |||||||||||
| xi | |||||||||||
| yi | |||||||||||
| |xi-yi| | |||||||||||
| НОД |
Из таблицы видно, что уже на 7-м шаге был найден делитель N, равный 19.
{Вычисление наибольшего общего делителя}
Function NOD(A as integer, B as integer) as integer
if (A mod B)=0 then
NOD=B
Else
NOD=NOD(B, A mod B)
End if
End
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что вычисляет алгоритм Евклида?
2. Сколько строчек вычислений необходимо произвести в алгоритме Евклида?
3. Как производится заполнение столбцов x и y в расширенном алгоритме Евклида?
4. Какая алгоритмически сложная задача лежит в основе метода RSA?
5. Что такое простое число? Какие методы проверки простоты числа вы знаете?
6. Как генерируется параметры метода RSA?
7. Какие параметры в RSA вычисляются с помощью алгоритма Евклида?
8. Как производится процедура шифрования/расшифровки в методе RSA?
9. Какой длины должны быть простые числа p и q в методе RSA, чтобы обеспечить необходимый уровень надежности?
10. Каким образом, зная значение функции Эйлера и открытый ключ е, можно рассчитать закрытый параметр d?
11. Дайте определение односторонней функции.
12. Сколько итераций потребуется сделать в методе Полларда, если N ≈100 млн (108)?
ЛИТЕРАТУРА:
1. С.Г.Баричев, В.В.Гончаров, Р.Е.Серов. Основы современной криптографии – Москва, Горячая линия – Телеком, 2001
2. А.В.Беляев. "Методы и средства защиты информации" (курс лекций). http://www.citforum.ru/internet/infsecure/index.shtml
3. А. А. Болотов, С. Б. Гашков, А. Б. Фролов, А. А. Часовских, «Алгоритмические основы эллиптической криптографии». Учебное пособие. М.: Изд-во МЭИ. 2000 г., 100 с.
4. А.Володин. «Кто заверит ЭЦП», журнал «Банковские системы», ноябрь 2000, http://www.bizcom.ru/system/2000-11/04.html
5. Т.Илонен. Введение в криптографию (Ylonen Tatu. Introduction to Cryptography), http://www.ssl.stu.neva.ru/psw/crypto/intro.html
6. Ш.Т. Ишмухаметов. Технологии защиты информации в сети, Казань, 2008, 91 с. http://depositfiles.com/files/e9zxcqos9
7. Н.Коблиц. Теория чисел и криптография, М.:, ТВР, 2001 http://gabro.ge/biblio/0708/0081/file/Cryptography/Koblic_-_Teoriya_Chisel_i_Cryptografiya.rar
8. О.Р. Лапонина. Криптографические основы безопасности, курс Интернет-университета, http://www.intuit.ru/department/security/networksec
9. Р.Лидл, Г.Нидеррайтер. Конечные поля, в 2 т., пер.с англ., М.: Мир, 1998, 438 с.
10. А.А. Молдовян, Н.А. Молдовян, Б.Я. Советов. Криптография. М., Лань, 2001
11. А.А. Молдовян, Н.А. Молдовян, Введение в криптосистемы с открытым ключом, БХВ-Петербург, 2005, с. 286 http://cyberdoc.nnm.ru/vvedenie_v_kriptosistemy_s_otkrytym_klyuchom
12. А.Г.Ростовцев. Алгебраические основы криптографии, СПб, Мир и Семья, 2000.
13. А.Г.Ростовцев, Е.Б.Маховенко. Теоретическая криптография. – СПб.: АНО, ПО “Профессионал”, 2005,http://bookpedia.ru/index.php?newsid=1265
14. Г.Семенов. «Цифровая подпись. Эллиптические кривые».
http://www.morepc.ru/security/crypt/os200207010.html?print
14. В.Столлингс. Основы защиты сетей. Приложения и стандарты, М.: Вильямс, 2002, 429 с.
15. Брюс Шнайер. Прикладная криптография, 2-е издание: протоколы, алгоритмы и исходные тексты на языке С, http://www.ssl.stu.neva.ru/psw/crypto/appl_rus/appl_cryp.htm
16. Dr. Michael Ganley, Thales eSecurity Ltd. Метод эллиптических кривых, http://www.racal.ru/rsp/eliptic_curve_cryptography.htm
17. В.М.Фомичев. Дискретная математика и криптология, Диалог-МИФИ, 2003, 399 с.
18. Сайт Криптографический ликбез - http://www.ssl.stu.neva.ru/psw/crypto.html
19. Jovan Dj. Golic. Cryptanalysis of Alleged A5 Stream Cipher, Beograd, Yugoslavia, http://jya.com/a5-hack.htm
20. Ю. Спектор. Использование инструментов криптографии в Delphi-приложе-ниях, http://www.delphikingdom.com/asp/viewitem.asp?catalogID=1271
