Алгоритм возведения в степень по модулю натурального числа

 

Для выполнения шифрования по методу RSA приходится выполнять возведение в большую степень различных чисел, а результат приводить по модулю числа N, являющегося параметром метода и имеющего длину 512 и более бит. Уже для небольших a и e вычислить значение

(1)

выполняя сначала возведение в степень, а потом вычисляя остаток от деления на N, становится невозможным. Между тем, если применить алгоритм, описанный в этом разделе, можно вычислять выражения (1), для достаточно больших чисел a, e, N, оставаясь в рамках обычных операций с целыми числами, заложенных в компьютере.

Алгоритм быстрого возведения в степень основывается на идее замены прямого вычисления возведения в степень последовательными операциями умножения на a и возведения в квадрат. Для этого представим степень e число в двоичном исчислении

(2)

где любое t_i для принадлежит , . Зная вектор разрядов , можно вычислить число e, применяя последовательные вычисления:

, (3)

Например, если e = 13, то в двоичном представлении e = 1101₂, и 13 можно представить как результат вычисления , .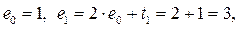

Последнее число и есть e.

Используя формулы (3), можно процедуру возведения в степень по модулю натурального числа N, записать в виде последовательности итераций:

где . Множитель в зависимости от принимает либо значение a, если , либо 1, если . Результат вычислений можно свести в таблицу

			...
			...

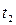
Пример. Вычислить .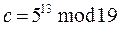

Решение. Переведем степень e=13 в двоичный вид. Для этого заполним следующую таблицу:

e div 2
e mod 2

Таблица 1. Перевод десятичного числа e к двоичному представлению.

Искомое двоичное разложение числа e будет во второй строке таблицы, записанное в обратном порядке справа налево.

 

Далее, составим таблицу вычисления с, заполняя следующую таблицу:

е
с

Таблица 2. Возведение а=5 в степень e=13 по модулю 19.

В первой строке запишем цифры двоичное разложения числа 13. В первую ячейку второй строки поместим основание а =5. Далее каждое следующее значение с будем вычислять по формуле:

Например,

 

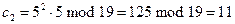
Приведем код на Паскале вычисления функции возведения в степень:

 

Function Rise(A,B,N:Integer):Integer;

var

B2:array[1..20] of byte;

i,C,L:integer;

Begin

C:=B; i:= 1;

While C > 0 do

Begin

B2[i]:= C Mod 2;

C:= C div 2;

i:= i + 1;

End;

L:= i - 1;

i:= 1;

D:= A;

While i <L do

Begin

D:= (D * D) Mod N;

If B2[L-i]= 1 Then D:=(D * A) Mod N;

i:= i + 1;

End;

Rise:= D;

End;

Генерация простых чисел

Для определения параметров RSA необходимо генерировать простые числа заданной длины. Известно, что на интервале [1; N ] число простых чисел равно примерно . Например, для N, равного 1 млн, число простых чисел в интервале от 1 до 10⁶, равно примерно 50 тысяч. Для генерации простых чисел можно выбрать произвольное нечетное число T и проверить его на простоту с помощью одного из тестов, описанных ниже. Если T окажется составным, то надо заменить его на T+2 и проверить снова затем проверить T+4 и т.д. В среднем, через шагов простое число будет найдено. Для генерации числа из заданного интервала [A; B] в Visual Basic можно использовать следующий алгоритм:

Function Generator(A as Integer, B as integer) As Integer

Randomize

t = Rnd() * (B - A) + A

Generator = t

End Function

 

1. Перебор делителей числа Т. Если число Т – составное, то найдется число k, меньшее , которое делит Т. Поэтому простейшим тестом на простоту является проверка делителей числа Т от 2 до . Приведем программу на Visual Basic:

Function Check_prime(T As Integer) As Boolean

Dim k as integer

Dim k As Integer

Dim i As Integer

Dim b As Boolean

b = True

k = Int(Sqr(T))

For i = 2 To k

If T Mod i = 0 Then

b = False

Exit For

End If

Next i

Test_prime = b

End function

2. Тест Ферма. Согласно теореме Ферма, если число Т – простое, то для любого . На обращении этой теоремы основан следующий вероятностный тест:

Если для произвольных различных k чисел a, меньших T, выполняется условие , то с вероятностью, не меньшей, чем 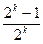, число a является простым.

 

К сожалению, полностью обратить теорему Ферма нельзя, т.к. существуют так называемые числа Кармайкла, для которых условие Ферма выполнено для всех a, меньших T, но числа являются составными. Однако, поскольку числа Кармайкла встречаются чрезвычайно редко, то в наших условиях можно ими пренебречь.

 

3. Тест Миллера Рабина. Пусть Т – произвольное число. Представим Т–1 в виде N–1=2^s∙t, где t – нечетно. Будем говорить, что число a отвергает число Т, если выполнено одно из двух условий:

а) Т делится на a,

б) и для всех целых k, .

Если найдется число а, отвергающее Т, то Т является составным. Тест Миллера выполняется следующим образом:

1. Выбираем случайное число a, 1 < a < Т, и проверим, что Т не делится на а нацело,

2. Проверим далее, что или найдется k, , такое, что

Если какое-то из условий 1 и 2 не будет выполнено, то число Т – составное, иначе, ответ не известен. Повторим процедуру с новым а.

После k циклов вероятность того, что Т – составное, меньше 4^-k, т.е. убывает очень быстро.