1. Разложить многочлены по степеням х–2: 
.
Решение:
1) Разделим исходный многочлен на двучлен х–2 с помощью схемы Горнера. Получим: 
.
Далее, неполное частное снова разделим на двучлен х–2 с помощью схемы Горнера. Получим:
.
Наконец, разделив новое неполное частное на двучлен х–2, получим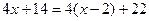 
.
Таким образом, получаем:
Результаты последовательного применения схемы Горнера приведены в таблице:
| –2 | –1 | |||
| 4·2–2=6 | 6·2+5=17 | 17·2-1=33 | ||
| 4·2+6=14 | 14·2+17=45 | |||
| 4·2+14=22 | ||||
Ответ: 
2. Освободиться от иррациональности в знаменателе: 
Решение:
Число 
есть значение многочлена 
при 
. Найдем многочлен, корнем которого является . Это, очевидно, многочлен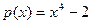 
. Применим к f(х) и р(х) алгоритм Евклида:
| 
| ||||||||||||||||||||
|   
| ||||||||||||||||||||
 –2
| |||||||||||||||||||||
| |||||||||||||||||||||
| |||||||||||||||||||||
| |||||||||||||||||||||
|
| 
| ||||||||||||||||||||
|
|  
| ||||||||||||||||||||
| |||||||||||||||||||||
| |||||||||||||||||||||
Эти многочлены взаимно просты, следовательно, существуют многочлены u(х) и v(х), такие, что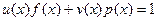 
. Полагая в этом равенстве , будем иметь: 
или 
- искомое представление для знаменателя дроби.
Найдем u(х) и v(х).
; 
.
Отсюда 
где 
, а 
.
Полагая в последнем равенстве , находим:
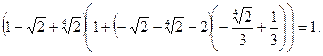
Раскрывая скобки во втором сомножителе, получаем:
или
.
Окончательно получаем:
Ответ: 
3. Отделить кратные множители многочлена
Решение:
Найдем производную многочлена f(х):
.
С помощью алгоритма Евклида найдем НОД многочлена и его производной.
1) 
| 
| |
| 
| |
| 
| |
| ||
| ||
| 
| |
 = 
| ||
2) 
|
| |||
|  
| |||
| 
| |||
| ||||
| ||||
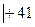
| : 400 | |||
 = 
| ||||
3) 
|
|
|
| 
|
| |
|
| |
Таким образом, последний, отличный от нуля остаток и есть наибольший общий делитель многочлена и его производной:
Следовательно, многочлен f(х) имеет 2 корня 2-й кратности: 
и 
.
Разделим многочлен f(х) с помощью схемы Горнера на 
и 
:
| –14 | –20 | –8 | ||||
| –1 | –2 | –12 | –8 | |||
| –1 | –4 | –8 | ||||
| –2 | –4 | |||||
| –2 | –2 |
Окончательно получаем:
Ответ: многочлен f(х) имеет 2 кратных корня ( и ) и один простой корень (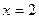
).
4. а) Решить уравнение 3-й степени, используя формулы Кардано: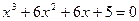 
.
Решение: освободимся от квадрата неизвестного, чтобы использовать формулы Кардано. Для этого введем новую переменную: 
. Отсюда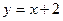 
. С помощью схемы Горнера разложим левую часть по степеням 
:
| –2 | –2 | |||
| –2 | –6 | |||
| –2 | ||||
| –2 |
Получим неполное кубическое уравнение 
.
Корни этого уравнения находятся по формулам Кардано:
, где 
,
.
Подставляем в формулы 
, 
. Получаем:
Так как u и v – различные действительные числа, то уравнение имеет 1 действительный и 2 комплексно сопряженных корня.
.
.
Так как 
, окончательно получаем:
, 
,
.
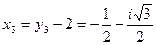Ответ: 
, 
, 
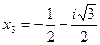
4. б) Решить уравнение 4-й степени методом Феррари: 
.
Решение: Левую часть уравнений представим в виде разности квадратов некоторого трехчлена и двучлена. Для этого будем считать 
квадратом 1-го члена трехчлена, 
– удвоенное произведение 1-го члена на 2-й и введем новую переменную λ в качестве 3-го члена:
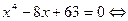
. Правая часть этого уравнения является квадратным трехчленом относительно переменной х. Подберем λ так, чтобы правая часть являлась полным квадратом. Для этого его дискриминант должен быть равен нулю:
.
Полученное уравнение называется кубической резольвентой данного уравнения 4-й степени. Для его решения достаточно найти один корень резольвенты. Преобразуя ее, получаем:
, 
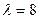. Подставим 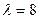в уравнение: 
;
;
;
;
.
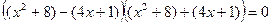Решая квадратные уравнения 
и 
,
Получаем корни: 
и 
.
Ответ: 
, 
, 
, 
.
5. Найти рациональные корни многочлена
Решение: так как многочлен не является нормированным, то он может иметь дробные корни, числители которых являются делителями свободного члена, а знаменатели – делителями старшего коэффициента. Таким образом, все рациональные корни многочлена можно искать среди чисел 
С помощью схемы Горнера найдем значения многочлена при 
:
| –34 | –17 | –6 | –6 | ||||
| –10 | –3 | –9 | |||||
| –1 | –58 | –99 | –76 |
Используем тот факт, что если дробь 
является корнем многочлена 
, то 
и 
– целые числа. Проверим это условие для выписанных чисел. Результаты запишем в таблицу:
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
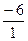
| ц | д | ц | д | д | д | ц | д | ц | д |
| д | д | д | ц |
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
|
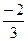
| ц | д | ц | д | д | д | ц | д | д | д |
|
| д | ц | ц |
|
| 
| 
| 
| 
| 
| 
| 
| 
|
|
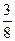
| д | д | д | д | д | д | д | д |
|
|
Рациональные корни следует искать среди чисел , и . Сделаем это с помощью схемы Горнера:
| –34 | –17 | –6 | –6 | ||||
|
| 
| 
| 
| 
| |||
|
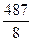
| –18 | –9 | –12 | ||||
|
| –12 |
Таким образом, многочлен имеет 2 рациональных корня: и .
Ответ: рациональными корнями многочлена являются числа и .
6. Выразить многочлен
через основные симметрические многочлены.
Решение. Представим данный симметрический многочлен 
в виде суммы симметрических многочленов: 
и каждое слагаемое выразим через основные симметрические многочлены.
1) Составим таблицу для первого слагаемого:
| Системы показателей | Возможные высшие члены многочлена
| Соответствующие произведения основных симметрических многочленов |
| 3 0 0 | 
| 
|
| 2 1 0 | 
| 
|
| 1 1 1 | 
| 
|
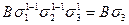
Здесь 
; 
; 
– основные симметрические многочлены.
Из данной таблицы получаем тождество: 
с неопределенными коэффициентами А и В. Для нахождения этих коэффициентов будем подставлять в полученное тождество различные числовые значения переменных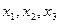 
. При этом удобнее подставлять такие значения, при которых некоторые из многочленов 
обращаются в 0. Эти вычисления также оформим в виде таблицы:
| х1 | х2 | х3 | σ1 | σ2 | σ3 | f(х) | φ(σ) | f(х)= φ(σ) |
| 8+2А | 8+2А=2 | |||||||
| –2 | –3 | –2 | –6 | –8В | –8В=–6 |
Получаем систему уравнений относительно неизвестных А и В:
Решив ее, получим А=–3, В=3.
Значит, 
2) Составим таблицу для второго слагаемого:
| Системы показателей | Возможные высшие члены многочлена
| Соответствующие произведения основных симметрических многочленов |
| 2 2 0 | 
| 
|
| 2 1 1 | 
| 
|
Из данной таблицы получаем тождество: 
с неопределенным коэффициентом А. Для нахождения этого коэффициента составим таблицу:
| х1 | х2 | х3 | σ1 | σ2 | σ3 | f(х) | φ(σ) | f(х)= φ(σ) |
| –1 | –4 | –12А | –12А=24 |
Получаем А=–2.
Значит, 
3) Окончательно получаем:
= 
=
Ответ:
.
7. Найти значение симметрического многочлена 
от корней уравнения 
:
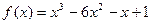
Решение: Выразим симметрический многочлен через основные симметрические многочлены. Нетрудно заметить, что 
. Выразим через основные симметрические многочлены первое слагаемое.
| Системы показателей | Возможные высшие члены многочлена
| Соответствующие произведения основных симметрических многочленов |
| 2 1 0 | 
| 
|
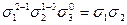
| 1 1 1 |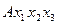 
| 
|
Из таблицы получаем тождество: 
с неопределенным коэффициентом А. Для его нахождения подставим в полученное тождество числовые значения переменных .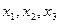
| х1 | х2 | х3 | σ1 | σ2 | σ3 | f(х) | φ(σ) | f(х)= φ(σ) |
| –2 | –3 | –2 | –2А | –2А=6 |
Отсюда получаем А=–3, т.е. 
, поэтому 
.
Для вычисления значения этого многочлена от корней данного уравнения 
, воспользуемся формулами Виета при п =3: 
, 
, 
.
Окончательно получаем: 
.
Ответ: значение многочлена значение симметрического многочлена от корней уравнения
равно –5.
8. Решить систему уравнений, сведя ее к симметрической введением новой переменной: 
Решение. Сделаем замену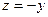 
. Тогда данная система запишется в виде (1) 
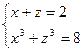– система двух симметрических уравнений. Обозначим 
, 
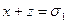. Так как 
, то система (1) может быть записана в виде (2) 
.
Последовательно решая эту систему, будем иметь:
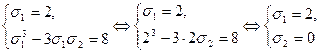
Возвращаясь к исходным переменным, получим:
Учитывая сделанную замену 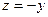, окончательно имеем 
Ответ: данная система имеет 2 решения: (2;0) и (0;–2).
ПРОГРАММА ЭКЗАМЕНА
