Многочлены одной переменной

Федеральное агентство по образованию

Южный федеральный университет

Педагогический институт

Кафедра алгебры и высшей математики

А.А. Авдеева

И.А. Гусева

И.Ю. Жмурова

Н.А. Поляков

 

Алгебра многочленов

Учебное пособие для самостоятельной работы студентов

 

 

Ростов-на-Дону

 

ББК 22.176я73

А – 77

Алгебра многочленов. Учебное пособие для самостоятельной работы студентов вузов и педколледжей. ПИ ЮФУ, 2010 – 28 стр.

 

Настоящее учебное пособие содержит задачи и упражнения по основным разделам курса «Алгебра» для студентов 3 курса. В пособии изложены основные теоретические сведения по алгебре многочленов, дана программа экзамена, приведено содержание контрольной работы, даны образцы решения типовых примеров и перечислены основные требования к выполнению контрольной работы.

Полезно студентам как очной, так и заочной форм обучения.

 

 

Ó А.А, Авдеева, И.А. Гусева, И.Ю. Жмурова, Н.А. Поляков, 2010 г.

 

СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ.. 4

СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ... 5

Многочлены одной переменной. 5

Схема Горнера. 5

Алгоритм Евклида. 6

Отделение кратных множителей. 6

Решение алгебраических уравнений 3-й и 4-й степеней. 7

Рациональные корни многочленов с целыми коэффициентами 7

Многочлены многих переменных. 8

Основная теорема теории симметрических многочленов. 8

Формулы Виета. 8

Системы уравнений. 9

ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ 10

ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ... 11

ПРОГРАММА ЭКЗАМЕНА.. 24

ЛИТЕРАТУРА.. 26

ВВЕДЕНИЕ

 

Настоящее пособие предназначено для студентов дневной и заочной формы обучения, изучающих раздел «Алгебра многочленов» курсов «Алгебра» или «Алгебра и теория чисел». Пособие включает в себя задачи и упражнения по всем темам курса.

Задачи и упражнения подобраны таким образом, чтобы закрепить основные теоретические сведения путем решения практических задач.

Кроме того, в пособии изложены основные требования к контрольным работам для студентов заочного отделения, контрольная работа и программа экзамена по курсу "Алгебра".

Приведенные в пособии задачи и упражнения могут быть использованы для составления контрольных заданий студентам-заочникам как математических специальностей, так и других, в частности, студентам факультета педагогики и методики начального обучения.

 

СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ

Многочлены одной переменной

Схема Горнера

1.1–1.5. Пользуясь схемой Горнера, разложить на простейшие дроби:
1.1.
1.2.
1.3.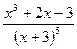
1.4.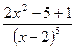
1.5.
1.6–1.8. Разложить многочлены по степеням х:
1.6.
1.7.
1.8.
1.9.	Определить коэффициент а так, чтобы многочлен 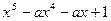имел –1 корнем не ниже второй кратности.
1.10.	Определить А и В так, чтобы многочлен делился на .

 

Алгоритм Евклида

2.1.–2.6. Пользуясь алгоритмом Евклида, подобрать М(х) и N(х) так, чтобы :
2.1.	;
2.2.	;
2.3.	;
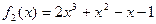
2.4.	;
2.5.	;
2.6.	;
2.7–2.10. Освободиться от иррациональности в знаменателе:
2.7.		2.9.
2.8.		2.10.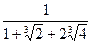

Отделение кратных множителей

3.1–3.10. Отделить кратные множители многочленов:
3.1.
3.2.
3.3
3.4
3.5.
3.6.
3.7.
3.8.
3.9.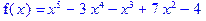
3.10.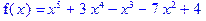

 

Решение алгебраических уравнений 3-й и 4-й степеней

а) Решить уравнение 3-й степени, используя формулы Кардано;

б) Решить уравнение 4-й степени методом Феррари

4.1	а)	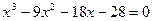б)
4.2	а)	б)
4.3	а)	б)
4.4	а)	б)
4.5	а)	б)
4.6	а)	б)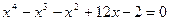
4.7	а)	б)
4.8	а)	б)
4.9	а)	б)
4.10	а)	б)

 

Рациональные корни многочленов с целыми коэффициентами

Найти рациональные корни многочленов:

5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8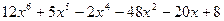
5.9
5.10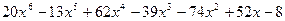