Використовують метод умовних моментів. Теорію використання методу для вивчення електричних параметрів геологічного середовища див. в підрозділі 7.1. Урахування структури тріщинно-порового простору відбувається за допомогою параметра форми a = с / а (a = 103–10–5), де с, а – півосі еліпсоїда вздовж і перпендикулярно до осі обертання. Пропонується дослідити два варіанти орієнтації ізотропних включень різних форматів в ізотропній матриці: перший – хаотична орієнтація включень, що відповідає ізотропній моделі; другий – односпрямована орієнтація включень, що відповідає анізотропній моделі. Крім цього, ураховуючи особливості методу умовних моментів, пропонується дослідити вплив цих параметрів в двох модифікаціях: "високоомна матриця і включення-провідники" та "матриця-провідник і високоомні включення".
Ефективна електропровідність геологічного середовища визначається співвідношенням

де 

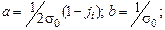



s1 – електропровідність включення; s2 – електропровідність матриці; с 1 – концентрація включень; с 2 – концентрація матриці.
Вихідні дані: електропровідність включення s1 і матриці s2.
Програмні засоби та їхнє використання: програма розрахунків ефективної електропровідності тріщинно-порового геологічного середовища.
Завдання: дослідити вплив на ефективну електропровідність геологічного середовища концентрації включень від 0 до 100 % принаймні для трьох різних форматів. При односпрямованих пустотах (анізотропна модель) будують графіки залежності s11, s33 і відношення s11/s33 від концентрації включень с 1. При хаотично розорієнтованих пустотах (ізотропна модель) будують графіки залежності sвід концентрації включень с 1. Розглянути два варіанти – високопровідної матриці та непровідних включень, і навпаки. Графіки побудувати в білогарифмічному масштабі.
Математичне моделювання дисперсії
й розсіювання пружних хвиль
у тріщинуватому геологічному середовищі
Геологічне середовище неоднорідне й дискретне. У ньому присутні неоднорідності з широким спектром характерних розмірів. Якщо в акустичному й ультразвуковому діапазонах розсіювання пружних хвиль спричиняють мікротріщини, зерна мінералів, мікрошаруватість, то в сейсмічному діапазоні це – мікротріщини, зони подрібнення, тонкошаруватість.
Численні методи математичного моделювання дисперсії й розсіювання пружних хвиль на структурних неоднорідностях геологічного середовища в реальному середовищі обмежуються невеликими концентраціями мікротріщин.
Метод моделює дисперсію та розсіювання пружних хвиль на неоднорідностях без будь-яких обмежень на їхню форму, властивості, концентрацію й базується на теорії статистичного усереднення з використанням методу умовних імовірностей.
Статичні ефективні модулі пружності
Геологічне середовище розглядатимемо як частково неперервне, пружні властивості структурних неоднорідностей якого є випадковими функціями просторових координат. Рівняння руху запишемо з урахуванням тензора напруги Коші лінійної теорії пружності
 (1)
(1)
де  – тензор напруги, r – щільність,
– тензор напруги, r – щільність,  – вектор зміщень. Тут індекс після коми означає диференціювання за відповідною просторовою змінною, а точки над буквою – диференціювання за змінною часу.
– вектор зміщень. Тут індекс після коми означає диференціювання за відповідною просторовою змінною, а точки над буквою – диференціювання за змінною часу.
Дослідимо гармонічний хвильовий рух типу
 (2)
(2)
 – діюча амплітуда пружних зміщень, w – кругова частота.
– діюча амплітуда пружних зміщень, w – кругова частота.
Використаємо закон зв'язку між напругами  і деформаціями
і деформаціями  в формі
в формі
 (3)
(3)
де  – тензор пружних сталих геологічного середовища. Деформації пов'язані з вектором пружних зміщень як
– тензор пружних сталих геологічного середовища. Деформації пов'язані з вектором пружних зміщень як
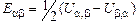 (4)
(4)
Підставляючи вирази (3), (4) в (1), одержимо
 (5)
(5)
Якщо геологічне середовище, в якому розповсюджується хвиля, неоднорідне, то тензор пружних сталих 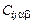 і щільність r є випадковими функціями просторових координат. Припустимо, що ці функції статистично однорідні в межах деякого об'єму V, лінійні розміри якого значно менші від довжини хвилі.
і щільність r є випадковими функціями просторових координат. Припустимо, що ці функції статистично однорідні в межах деякого об'єму V, лінійні розміри якого значно менші від довжини хвилі.
Якщо 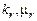 – модулі об'ємного стиснення і зсуву r -компоненти, а включення мають сфероїдальну форму із співвідношенням півосей æ і рівномірно розорієнтованих в просторі, то для розрахунку статичних ефективних пружних сталих
– модулі об'ємного стиснення і зсуву r -компоненти, а включення мають сфероїдальну форму із співвідношенням півосей æ і рівномірно розорієнтованих в просторі, то для розрахунку статичних ефективних пружних сталих  геологічного середовища із сфероїдальними включеннями одержимо формули
геологічного середовища із сфероїдальними включеннями одержимо формули
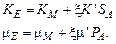 (6)
(6)
Тут прийнято позначення:

| 
| 
| 
|
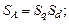
| 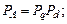
| 
| 
|

| 
| 
|  (7) (7)
|
Вирази (7) можна використовувати як у випадку твердих включень сфероїдальної форми, так і при обчисленнях ефективних пружних сталих геологічного середовища, які мають пори та мікротріщини.






