Краткие теоретические сведения. «Представление графической информации (ГИ) и базовые операции с ней»

«Представление графической информации (ГИ) и базовые операции с ней»

 

Наиболее важно сразу понять, как представляется ГИ и операции работы с ней в компьютере (кратко для случая двухмерного пространства). Этот материал базовый, он понадобится Вам для выполнения лабораторных работ, курсовой работы, при ответе на вопрос на экзамене. Краткая справка по этому поводу.   Преобразование точки Точка на плоскости представляется двумя координатами: |x y|. Матрица преобразования точки – квадратная, (2*2). Ниже показано преобразование точки через квадратную матрицу; здесь xn = xa + yc и yn = xb + yd – новые координаты точки после преобразования.   Преобразование фигуры Если представить фигуру как совокупность точек, то можно провести и ее преобразование. В следующем примере задано четыре точки: A(0, 0), B(1, 0), C(1, 1), D(0, 1), каждая из которых после преобразования переходит соответственно в A*(0, 0), B*(a, b), C*(a + c, b + d), D*(c, d). Геометрически это соответствует деформации фигуры. Для экономии машинного времени обычно в аффинной геометрии просчитывают только координаты вершин. Согласно свойствам аффинных преобразований прямые линии будут сохраняться. Поэтому потом вершины соединяют в том же порядке, что и до преобразования. При этом площадь новой фигуры равна площади старой фигуры, умноженной на детерминант матрицы преобразования: S2 = S1 * |ad - bc|.

 

,

 

Однородные координаты Любая система координат, в которой представление точки в двухмерном пространстве задается при помощи трех координат (Р1, Р2, Р3), называется системой однородных координат. Вообще, для n-мерного пространства число однородных координат должно быть на единицу больше: n + 1. Применение однородных координат в общем случае позволяет устранять аномалии, возникающие при работе в декартовых координатах, и представлять сложные преобразования в виде произведения нескольких матриц. Геометрическая интерпретация на случай двухмерного пространства: введение третьей координаты, равной единице, можно трактовать как переход в трехмерное пространство, в котором разрешено работать только в плоскости z = 1. Следует представлять себе, что экран компьютера (картинная плоскость, плоскость изображения) находится в плоскости z = 1. В случае выхода рисунка за сечение z = 1 рисунок возвращается принудительно в данное сечение – для того, чтобы были возможны последующие операции. Математически это означает деление всех компонент вектора координат на третью компоненту, при этом третья становится равной 1. Такая операция называется нормализацией однородных координат.

 

 

Общий вид преобразования

Операция cмещения

Матрица преобразования содержит в себе константы m и n, под действием которых точка смещается на m единиц вдоль оси x и на n единиц - вдоль оси y:

 

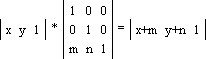
Операция масштабирования За счет коэффициентов a и d матрицы преобразования происходит увеличение (или уменьшение) значения координат точки (x, y) в a и d раз по осям x и y соответственно:     Общее полное масштабирование В данном случае при s < 1 будет происходить увеличение значения координат точки (x, y) в s раз; при s > 1 мы получим обратный эффект - уменьшение значения координат (x, y) в s раз.   Поворот на угол q Здесь q - угол, на который требуется повернуть точку (x, y). Обратите внимание: поворот происходит относительно точки (0, 0) против часовой стрелки!   Для примера разберем небольшое задание. Повернуть треугольник на угол q = 90o. Возьмем следующие координаты точек (вершин) треугольника: A(3, -1), B(4, 1), C(2, 1). Угол поворота равен 90o, следовательно, матрица поворота: Теперь, подставляя данные, имеем Результат на экране будет таким:   Зеркалирование Существуют различные варианты зеркалирования, например, матрица для зеркалирования относительно прямой y = x:   Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол a Чтобы провести любое сложное преобразование, необходимо разложить его на базовые операции. Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол a состоит из трех базовых операций: 1) перенос фигуры на вектор A(-m, -n) для совмещения точки (m, n) с началом координат; 2) поворот фигуры на угол a; 3) перенос фигуры на вектор A'(m, n) для возвращения ее в исходное положение. Так как фигуру можно представить набором точек, то операции 1) - 3) можно выполнять последовательно для каждой точки. Покажем это на примере. Пусть мы хотим повернуть треугольник с координатами A(x, y), B(x1, y1), C(x2, y2) вокруг точки D(m, n) на угол a. Пусть P-s - матрица переноса точки на вектор A(-m, -n), Va - матрица поворота на угол a, Ps - матрица переноса точки на вектор A'(m, n). Итак, мы имеем все данные, необходимые для проведения сложного преобразования первой точки - A(x, y): Точно такие же преобразования необходимо провести для оставшихся двух точек треугольника, подставляя соответствующие их координаты взамен x и y (последовательность операций см. на рис. 1.6). Таким образом, сложная операция разбивается на простейшие и задается произведением соответствующих матриц преобразования, причем порядок действий существенно определяет результат.   Центральное проецирование (перспектива) px + qy + 1 = H - плоскость.   Важно отметить, что - в общем случае от перемены матриц местами результат меняется; - матрицы операций, идущие подряд, можно перемножать раздельно, главное - не менять их порядок следования (см. примечание 1); - линии при описанных выше (аффинных) преобразованиях переходят в линии. Поэтому обычно производится пересчет только координат вершин фигуры, а после этого соответствующие вершины в результирующей фигуре соединяются, как и в исходной фигуре.

 

 

Приложение 3.

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

 

Задача 1

Рассчитать в однородных координатах новое положение фигуры АВС при повороте ее на угол 30 градусов в двухмерном пространстве вокруг точки В.

А(3,3), В(6,3), С(4,1).

Решение и ответ задачи 1.

3 3 1 6 3 1 4 1 1

*

0,85 0,52 0 -0,52 0,85 0 2,46 -2,67 1

=

3,45 1,44 1 6,00 3,00 1 5,34 0,26 1

 

 

Задача 2

Вычислите, как выглядит трехмерный куб со стороной равной 2, установленный одной вершиной в начало трехмерных координат, с ребром, совпадающим с осью ОY, и перпендикулярным ему ребром, лежащим в плоскости ZOX под углом 45 градусов к оси Х при перспективном проецировании его на плоскость XOY из точки (z_c=10, y_c=0, x_c=0)

 

0 0 0 1 1.41 0 1.41 1 0 0 2.82 1 -1.41 0 1.41 1 0 2 0 1 1.41 2 1.41 1 0 2 2.82 1 -1.41 2 1.41 1

*

1 0 0 0 0 1 0 0 0 0 0 -0.1 0 0 0 1

=

0 0 0 1 1.41 0 0 0.859 0 0 0 0.718 -1.41 0 0 0.859 0 2 0 1 1.41 2 0 0.859 0 2 0 0.718 -1.41 2 0 0.859

=

0 0 0 1 1.64 0 0 1 0 0 0 1 -1.64 0 0 1 0 2 0 1 1.64 2.33 0 1 0 2.79 0 1 -1.64 2.33 0 1

 

Изобразите в осях XOY полученную фигуру, согласно вычисленным координатам (третий и четвертый столбцы отбросьте). Поставьте точки, следы вершин куба на плоскости XOY, и соедините их отрезками, проекциями ребер (1 и 2, 2 и 3, 3 и 4, 4 и 1, 5 и 6, 6 и 7, 7 и 8, 8 и 5, 1 и 5, 2 и 6, 3 и 7, 4 и 8). Объясните, почему в проекции невидима нижняя грань куба и видима верхняя грань куба снизу.

Задача 3.

Начертите фрактальным методом лист дерева. Постройте компьютерным способом или вручную 3-4 итерации. Перечислите параметры изображения. Примените подмешивание к одному из параметров случайных чисел для увеличения реалистичности изображения.

Пример программы и изображения разобран в книге Л.Аммерала «Программирование графики на турбо СИ» на стр. 128..

 

Задача 4.

Преобразуйте полилинию А(200,-100), В(100,200), С(-50,300), Д(20,-50), Е(-100,100) так, чтобы она, не потеряв пропорциональности, вместилась в экран компьютера размером (1024,768). Найдите координаты точек АВСДЕ на экране.

Для того чтобы выполнить масштабирование, необходимо:

• задать или определить координаты размера изображения: x_min, y_min, x_max, y_max и координаты области вывода: X_min, Y_min, X_max, Y_max;

x_{min= -50}, y_min=-100, x_max=200, y_max=300

X_min=1, Y_min=1, X_max=1024, Y_max=768

• вычислить коэффициенты масштабирования:
  f_x = (X_max - X_min) / (x_max - x_min)=(1024-1)/(200+50)=4.092,
  f_y = (Y_max - Y_min) / (y_max - y_min)=(768-1)/(300+100)= 1.9175,
  f_x = f_y = min(f_x, f_y) = min(4.092, 1.9175)= 1.9175
• произвести вычисление координат точек на экране: точка А (480,1), то есть

x_э = X_min + f_x * (x_р - x_min)=1+1.9175*(200+50)=480,
y_э = Y_min + f_y * (y_р - y_min)=1+1.9175*(-100+100)=1,
где x_э, y_э - экранные координаты, x_р, y_р - реальные координаты.

 

Задача 5.

Сколько цветов можно одновременно наблюдать на экране монитора, если под один пиксель в памяти будет отведено 3 байта, 2 байта, 1 байт? Сколько места в памяти занимает изображение, если разрешение монитора 1024*768? Ответ дать в виде таблицы.

Количество пиксел экрана = 1024*768=786432

Байт на пиксель	Количество цветов	Объем памяти в байтах	Объем памяти в Кбайтах
1байт= 8 бит	28=256	786432*1=786432	786432/1024=768Кб
2байт= 16 бит	216=65536	786432*2=1572864	1572864/1024= 1536Кб/1024=1,5Мб
3байта= 24 бит	224 =	786432*3=2359296	2359296/1024= 2304Кб/1024=2,25Мб

 

Задача 6.

Два треугольника с координатами вершин К(0,0,-10), Л(100,0,-100), М(50,50,-100) и П(0,40,-80),Р(40,40,-80),С(20,20,-120) наблюдаются с точки А(0,10,100) в трехмерном пространстве. Нарисуйте, как выглядит буфер кадра и z-буфер в памяти компьютера. Цвет КЛМ закодирован 1, цвет ПРС закодирован 2, цвет фона закодирован 0.

Спроецируйте треугольники на плоскость изображения (z=0) центральным проецированием (см. задачу 2). Переведите изображение в экранные координаты (см. задачу 4). Заполните буфер кадра цветами, учитывая границы фигур.

Для заполнения Z-буфера определите параметры плоскости (a,c) каждого треугольника ax + by + cz + d = 0 методом Ньюэла:

a = S(y_i - y_i+1) * (z_i + z_i+1)
b = S(z_i - z_i+1) * (x_i + x_i+1)
c = S(x_i - x_i+1) * (y_i + y_i+1).

При заполнении буфера по строке используйте формулу z:= z - (a/c). Учитывайте границы треугольников.

Рекомендация – загрузите проект «Z-буфер» из лекции 21.

 

Задача 7.

Рассчитайте освещенность точки (10,10,10) на отшлифованной серебряной пластинке, параллельной плоскости XOZ координат, которую освещает источник синего цвета силой 100, находящийся в точке (30,30,10). Атмосферу не учитывать. На сколько отличается освещенность этой точки от освещенности точки на краю пластины (-10,10,10)?

Поскольку пластина металлическая и отшлифована, то отражение зеркальное. Длина волны синего света l = 2нм. Угол падения луча находится в плоскости XOY и составляет (30-10)/(30-10)=tg(a), a=45град..

Формула Б.-Т. Фонга для расчета освещенности I_s = I_l * w(i, l) * cosⁿa,

где I_s - интенсивность света, попавшего в глаз наблюдателя, I_l - интенсивность падающего света, равна 100, w(i,l) - кривая отражения, представляющая отношение зеркально отраженного света к падающему как функцию угла падения i и длины волны l, коэффициенты 0,2 и 0,9 (см.рис.24.3 электронных лекций), a - угол между направлением света и нормалью к поверхности, равен 45 град., n - степень, аппроксимирующая пространственное распределение зеркально отраженного света, 5.

Так как для угла падения (30-10)/(30-10))=20/20=1,

Поскольку a=45 град, то и угол падения равен 45 град.. Тогда освещенность точки

I_s = 100 * 0,2*0,9 * cos⁵(45)=3.24, так как cos(45)=0,71 и cos⁵(45) = 0.18.

Во втором случае (30-10)/(30-(-10))=20/40=0,5,

угол падения = pi/2 – arctg(0.5) = 1.107 рад.

cos(1.107)=0.45

cos⁵ (1.107)=0.018

I_s = 100 * 0,2*0,9 * cos⁵(1,107)=0,324.

Очевидно, что освещенность уменьшилась в 10 раз. Данный результат характерен для отражения света на металле, так как пятно освещенности сфокусировано в небольшой области пространства в виде блика.