2.1 Вычисление алгебраического уравнения методом половинного деления
Метод деления отрезка пополам является одним из простейших методов нахождения корней нелинейных уравнений вида 
. Он состоит в следующем. Допустим, что нам удалось найти отрезок 
, на котором расположено искомое значение корня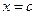 
, т. е. 
. В качестве начального приближения корня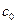 
принимаем середину этого отрезка: 
. Далее исследуем значения функции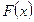 
на концах отрезков 
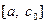и 
т. е. в точках 
. Тот из отрезков, на концах которого 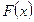принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка 
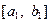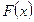. Вторую половину отрезка , на которой знак не меняется, отбрасываем. В качестве первого приближения корня принимаем середину нового отрезка 
и т. д. Таким образом, k-е приближение вычисляется как
после каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k итераций он сокращается в 
раз:
Пусть приближенное решение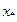 
требуется найти с точностью до некоторого заданного малого числа 
:
Взяв в качестве приближенного решения k-e приближение корня: 
, запишем с учетом обозначения 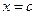с в виде
Итерационный процесс нужно продолжать до тех пор, пока не будет выполнено условие:
В приложении представлена программа для решения нелинейного уравнения x3+3x2-6x-1=0 методом деления отрезка пополам, выполненная на языке программирования C++.
Рисунок 1 Решение уравнения
методом половинного деления
Рисунок 2 Интерфейс решения программы
методом половинного деления
2.2 Решение дифференциальных уравнений. Модифицированный метод Эйлера.
Решить дифференциальное уравнение у/=f(x,y) численным методом - это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что
уi=F(xi)(i=1,2,…, n) и F(x0)=y0. (1)
Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Рассмотрим дифференциальное уравнение первого порядка (1) с начальным условием
x=x0, y(x0)=y0 (2)
Требуется найти решение уравнения (1) на отрезке [а,b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х0, х1, х2,…, хn, где xi=x0+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(хi)»yi вычисляются последовательно по формулам уi+hf(xi, yi) (i=0,1,2…).
При этом искомая интегральная кривая у=у(х), проходящая через точку М0(х0, у0), заменяется ломаной М0М1М2… с вершинами Мi(xi, yi) (i=0,1,2,…); каждое звено МiMi+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (1), которая
проходит через точку Мi. Если правая часть уравнения (1) в некотором прямоугольнике R{|x-x0|£a, |y-y0|£b}удовлетворяет условиям:
|f(x, y1)- f(x, y2)| £ N|y1-y2| (N=const), (3)
|df/dx|=|df/dx+f(df/dy)| £ M (M=const),
то имеет место следующая оценка погрешности:
|y(xn)-yn| £ hM/2N[(1+hN)n-1], (4)
где у(хn)-значение точного решения уравнения (1) при х=хn, а уn- приближенное значение, полученное на n-ом шаге.
На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2. Погрешность более точного значения уn* оценивается формулой
|yn-y(xn)|»|yn*-yn|. (5)
Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.
В приложении представлена программа для вычисления дифференциального уравнения методом Эйлера у=х3-у3, у(0,1)=0,5, [0,1;0,6],h=0,05, выполненные на языке программирования C++.
Рисунок 3 Решение уравнения
методом Эйлера
Рисунок 4 Интерфейс решения программы
методом Эйлера
2.3 Умножение матрицы на вектор
По определению произведения матриц умножение возможно только в том случае, если количество столбцов первого множителя равно количеству строк второго. Следовательно, вектор-строку удастся умножить только на матрицу, в которой столько же строк, сколько элементов в вектор-строке. Аналогично, вектор-столбец можно умножить только на матрицу, в которой столько же столбцов, сколько элементов в вектор-столбце.
Умножение матриц некоммутативно, то есть если A и B —матрицы, то A*B ≠ B*A. Более того, существование произведения A*B вовсе не гарантирует существования произведения B*A. Например, если матрица A имеет размеры 3*4, а матрица B — 4*5, то произведение A*B —матрица размером 3*5, а B*A не определено.
Пусть задан: вектор-строка A = [a1, a2, a3 … an] и матрица B размерности n*m, элементы которой равны: [b11, b12, b13, … b1m; b21, b22, b23, … b2m; … bn1, bn2, bn3, … bnm].
Тогда произведение A*B будет вектор-строкой размерности 1*m, причем каждый элемент ее равен:
Cj = ∑ai*bij (i = 1 … n, j = 1 … m)
Иными словами, для нахождения i-того элемента произведения нужно умножить каждый элемент вектора-строки на соответствующий ему по порядку элемент i-того столбца матрицы и просуммировать эти произведения.
Аналогично, если задана матрица A размерности m*n и вектор-столбец B размерности n*1, то их произведение будет вектором-столбцом размерности m*1, i-тый элемент которого равен сумме произведений элементов вектора-столбца B на соответствующие им элементы i-той строки матрицы A.
В приложении представлена программа для умножения матрицы A на вектор B, выполненные на языке программирования C++.
Рисунок 5 Решение умножения матрицы на вектор
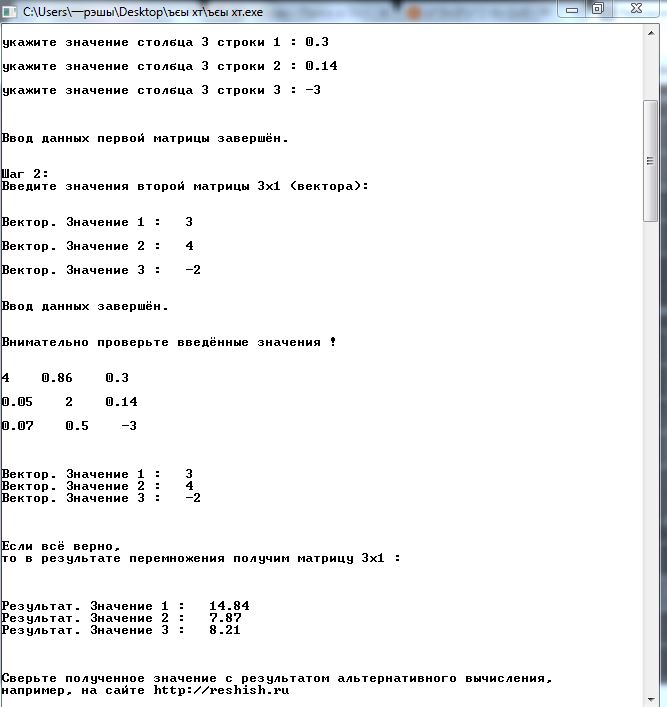
Рисунок 6 Интерфейс решения программы
умножения матрицы на вектор
 |
3.Блок-схемы программы
 |
3.1. Блок-схемы программы вычисления уравнения методом половинного деления.
3.2. Блок-схема программы вычисления уравнения
3.2. Блок-схемы методом Эйлера
3.3. 
Блок-схема программы вычисления умножения
матрицы на вектор
Заключение
В заключение хотелось бы отметить, что методы структурного программирования позволяют более мобильно и качественно проводить работу по модернизации программного обеспечения. Так достаточно усовершенствовать отдельный модуль откомпилировать его и главный модуль, для достижения, желаемого результата. Более того, текст главной программы более читаем, и занимает меньше места. Имеющиеся наработки в отдельных модулях можно использовать в других про граммах, не задумываясь об их работоспособности. Четко вычерченная структура позволяет яснее представить цели и задачи стоящие перед программистом. Не нужно все время перемещаться по тексту взад и вперед. В любой промежуток времени работы над очень большой программной появляется возможность сконцентрироваться на отдельном модуле. Открывается возможность совместной работы нескольких человек над одной громоздкой программной. Удачно разработанный модуль одного программиста становиться, доступен другим.
Все выше перечисленное позволяет сделать вывод. Что структурное программирование открывает не объятые просторы в развитии современной техники, и будущее, а вернее сказать уже настоящее именно за ним. Вместе с объектно-ориентированным программированием оно уже составляет авангард современной науки.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Информатика: учебник для вузов / А.Н. Гуда [и др.]; под ред. В.И. Колесникова. – М.: Дашков и К, 2008. – 400 с.
2. Чекмарев, Ю.В. Вычислительные системы, сети и телекоммуникации [Электронный ресурс]/ Ю.В. Чекмарев.– «ДМК Пресс», 2010.– 184 с. Режим доступа: http://e.lanbook.com/books/element.php?pl1_cid=258&pl1_id=1108.
3. Шаньгин, В.Ф. Защита компьютерной информации [Электронный ресурс]/ В.Ф. Шаньгин.– «ДМК Пресс», 2010.–544 с. Режим доступа: http://e.lanbook.com/books/element.php?pl1_cid=258&pl1_id=1146.
4. Галявов, И.Р. Borland C++ для себя [Электронный ресурс]/ И.Р.. Галявов. – «ДМК Пресс», 2009.– 214 с.. Режим доступа: http://e.lanbook.com/books/element.php?pl1_cid=258&pl1_id=1230.
5. Буч, Г., Рамбо Д., Якобсон И.Язык UML руководство пользователя [Электронный ресурс]/ Г.Буч, Д. Рамбо, И. Якобсон. – «ДМК Пресс», 2008.– 496 с. Режим доступа: http: //e.lanbook.com/books/element.php?pl1_cid =258&pl1_id =1246.
6. OpenOffice.org для профессионала [Электронный ресурс].– «ДМК Пресс», 2009. – 448 с. Режим доступа: http: //e.lanbook.com/books/ element.php?pl1_cid =258&pl1_id =1223.
7. Дьяконов, В.П. MATHLAB 9.5 /10/11 в математике, физике и образовании [Электронный ресурс]/ В.П.Дьяконов. –«ДМК Пресс»,– 2010.–752 с. Режим доступа: http: //e.lanbook.com/books/ element.php?pl1_cid =258&pl1_id =1181.
 |
ПРИЛОЖЕНИЕ
1. #include <iostream>
2. using namespace std;
3.
4. int Function_3() {
5. float h;
6. float a;
7. float b;
8. float n;
9. float x[100]; // резервируем массив значений переменной.
10. float y[100]; // резервируем массив значений переменной.
11. cout << "\n Решение дифференциального уравнения методом Эллера \n";
12. cout << "Уравнение y'=x^3-y^3 y(0.1)=0.5 \n\n\n";
13. y[1]=0.5; // известное решение уравнения по условию задачи. Первый элемент в массиве.
14. cout << "введите интервал значения Х [a;b] и шаг h \n";
15. cin >> a;
16. cin >> b;
17. cin >> h;
18. n=(b-a)/h; // определяем количество циклов.
19. for (int i = 0; i <= n+1; i++) {
20. x[i] = a; // заносим значение Х в массив
21. a=a+h;
22. }
23. cout << "число циклов равно " << n << "\n\n"; // проверяем правильность количества циклов
24. for (int i = 0; i <= n; i++) {
25. cout << "X(" << i <<") = " << x[i] <<"\n"; // проверяем значение Х в массиве
26. }
27.
28. cout << "\n\n";
29. for (int i = 1; i <= n+1; i++) {
30. y[i+1]=y[i]+h*(x[i]*x[i]*x[i]-y[i]*y[i]*y[i]); // дифференциальное уравнение собственной персоной.
31. cout << "X(" << i-1 <<") = " << x[i-1] << " Y(" << i-1 << ")= " << y[i] <<"\n";
32. }
33. for (int i = 1; i <= n+1; i++) {
34. y[i+1]=y[i]+h*(x[i]*x[i]*x[i]-y[i]*y[i]*y[i]); // дифференциальное уравнение собственной персоной.
35. cout << x[i-1] <<"\n";
36. }
37. 
for (int i = 1; i <= n+1; i++) {
38. y[i+1]=y[i]+h*(x[i]*x[i]*x[i]+y[i]*y[i]*y[i]); // дифференциальное уравнение собственной персоной.
39. cout << y[i] <<"\n";
40. }
41. return 0;
42.
43.
44. }
45.
46. int Function_2() {
47. cout << "\n---Программа перемножения матриц---\n";
48. cout << "Пожалуйста,дайте исходные данные: \n";
49. cout << "матрица размерности 3х3 и матрица-вектор размерности 3x1. \n";
50.
51. float Matrix[3][3]; // объявляем переменную массива размерности 3х3.
52. float vector[3]; // объявляем переменную массива 3x1
53. float vector_new[3]; // обявляем массив для результирующего значения.
54. cout << "\nШаг 1,Аккуратно введи данные матрицы 3x3: \n";
55. for (int i = 0; i <= 2; i++) {
56. for (int j = 0; j <= 2; j++) {
57. cout << "укажите значение столбца " << i + 1 << " строки " << j + 1 << ": "; // выводим на экран подсказку, и изменяем нумерацию для наглядности.
58. cin >> Matrix[i][j]; // ожидаем ввода элемента массива.
59. cout << "\n";
60. }
61. }
62.
63. cout << "\n \nДанные первой матрицы записал,а отменить несможешь;D.\n\n\n";
64. cout << "Шаг 2: \n";
65. cout << "Введите значения второй матрицы желательно без ошибок 3x1 (вектора): \n \n \n";
66. for (int x = 0; x <= 2; x++) {
67. cout << "Вектор. Значение "<< x + 1 << ": "; // Для удобства пользователя изменяем нумерацию строк..
68. cin >> vector[x];
69. cout << "\n";
70. }
71.
 |
72. cout << " \nВвод данных завершён.\n\n\n";
73. cout << "Внимательно проверьте введённые значения! \n \n \n";
74. for (int j = 0; j <= 2; j++) {
75. for (int i = 0; i <= 2; i++) { //выводим на экран матрицу в привычном для человека виде.
76. cout << Matrix[i][j] << " "; // столбцы и строки не могут быть "нулевыми" по счёту.
77. }
78. cout << "\n\n";
79.
80. }
81. cout << "\n\n";
82. for (int x = 0; x <= 2; x++) {
83. cout << "Вектор. Значение "<< x + 1 << ": " << vector[x] << "\n"; // строки не могут быть "нулевыми" по счёту.
84. }
85. cout << "\n\n\nЕсли всё верно,хотя мы ее получим в лбом случае главное что бы результат устраивал \n";
86.
87. cout << "в результате перемножения получим матрицу 3x1: \n";
88. for (int j = 0; j <= 2; j++) {
89. float result = 0.0; // переменная result действует только в этом цикле.
90. for (int i = 0; i <= 2; i++) {
91. result = result + Matrix[i][j]*vector[i]; // математика перемножения матрицы на вектор.
92. }
93. vector_new[j] = result; // присваиваем полученное значение результирующему вектору.
94. }
95.
96. cout << "\n\n\n";
97. //cout << setprecision(7);
98. /* используя cout для вывода значений с плавающей точкой,
99. обычно нельзя сделать каких-либо предположений о том, сколько цифр будет выводить cout no умолчанию.
100. Однако, используя манипулятор setprecision, вы можете указать количество требуемых цифр. */
101. for (int x = 0; x <= 2; x++) {
102. cout << "Результат. Значение "<< x + 1 << ": " << vector_new[x] << "\n"; // строки не могут быть "нулевыми" по счёту.
103. }
104. 
cout << "\n\n\n Открой программу рабочую написанную другим человеком,ибо все познается в сравнении, \n";
105.
106. cout << "например, на сайте http://reshish.ru \n";
107.
108. return 0; // возврат в основную программу.
109. }
110.
111. int Function_1() {
112. // подпрограммма решения нелинейного уравнения методом половинного деления
113. float a; // левая граница интервала
114. float b; // правая граница интервала
115. float a1; // левая граница интервала для отображения в решении
116. float b1; // правая граница интервала для отображения в решении
117. float sigma; // значение погрешности вычисления
118. float max_step; // ограничение количества шагов вычислений для индикации процесса вычисления
119. float xm; // середина интервала
120. float f_a; // значение функции в начале интервала
121. float f_b; // значение функции в конце интервала
122. float f_xm; // значение функции в середине интервала
123. int k; // целая часть функции f_xm
124. cout << "\n---Программа решения уравнения методом половинного деления---\n\n";
125. cout << "Шаг 1:\nВвод исходных значений.\n";
126. cout << "Задано уравнение x^3+3*x^2-6x-1=0\n\n";
127.
128. cout << "введите начальное значение исследуемого интервала:\n";
129. cin >> a;
130. a1=a;
131. cout << "\nвведите конечное значение исследуемого интервала:\n";
132. cin >> b;
133. b1=b;
134. cout << "\nвведите значение погрешности вычисления результата: например, 0.0001 \n";
135. cin >> sigma;
136. cout << "\nвведите ограничение количества шагов: например, 1000 \n\n";
137. cin >> max_step;
138. //cout.precision(7); // определяем вывод семизначных значений с плавающей точкой.
139. cout << "Шаг 2:\nпроверьте правильность введённых значений:";
140. 
cout << "\nначало интервала = " << a << "\nконец интервала = " << b << "\nзаданная точность = " << sigma << "\nограничение количества шагов = " << max_step;
141. cout << "\n\nШаг 3:\nРешение:\n";
142. for (int i = 0; i <= max_step; i++) {
143. if (b-a > sigma) { // продолжаем считать пока значения границ интервала различаются больше, чем на значение погрешности
144. xm=(a+b)/2; // вычисляем середину интервала
145. f_a = a*a*a+3*a*a-6*a-1; // вычисляем значение функции в начале интервала
146. // f_b = b*b*b+3*b*b-6*b-1; // вычисляем значение функции в конце интервала (можем не считать)
147. f_xm = xm*xm*xm+3*xm*xm-6*xm-1; // вычисляем значение функции в середине интервала
148. k=f_xm; // так как значение функции может никогда не стать равным "0", то необходимо остановиться, когда целая часть числа станет равна "0". Перемненная "k" имеет формат "int".
149. if (f_a*f_xm <= 0) { // если произведение больше нуля, значит смены знака функции не произошло на этом интервале
150. b=xm; // исключаем правый интервал и начинаем сначала
151. cout << "\nb = " << b << " Шаг i = " << i+1 << " решение слева ";
152. }
153. else {
154. a=xm; // исключаем левый интервал
155. cout << "\na = " << a << " Шаг i = " << i+1 << " решение справа ";
156. }
157. }
158. }
159. if (k == 0) {
160. xm=(a+b)/2; // вычисляем середину интервала для конечного решения
161. f_xm = xm*xm*xm+3*xm*xm-6*xm-1; //вычисляем значение функции для конечного решения
162. cout << "\n\nрешением уравнения на интервале от " << a1 << " до " << b1 << " является Х = " << xm << "\n\nзначение функции в этой точке = " << f_xm << "\n\n";
163. }
164. else {
165. cout << "\n\nПрограмма не смогла найти решение уравнения на заданном интервале значений.\nПопробуйте расширить интервал или проверьте с помощью графического метода,\nчто функция точно меняет знак на выбранном интервале.\n\n\n";
166.
 |
167. }
168. cout << "\n\nПроверьте решение уравнения альтернативным способом, напаример, используя сайт http://www.wolframalpha.com \n\n\n";
169.
170. return 0;
171. }
172.
173. int main() {
174. setlocale(0,"");
175. int menu = 5; // объявляем переменную "menu".
176. if (menu!= 0){
177. cout << "\n Аккуратно от этого будет зависить что будешь решать обдумай и нажми на кнопку \n";
178. cout << "\n";
179. cout << " нажмите 1 для выполнения первой подпрограммы \n";
180. cout << " нажмите 2 для выполнения умножения матрицы на вектор \n"; // выводим на стандартное устройство (экран) пояснения "Меню".
181. cout << " нажмите 3 для решения дифференциального уравнения методом Эйлера \n";
182. cout << " нажмите 0 для выхода из программы \n";
183.
184. cin >> menu; // ожидаем выбора и присваиваем значение переменной 'menu'.
185.
186. switch (menu) { // специальная конструкция, удобная для организации меню.
187.
188.
189. case 1: // сравнивает переменную "menu" с константой после служебного слова "case".
190. cout << "\n Вы ввели цифру: 1,ну что ж приступим \n"; // в случае совпадения выполняет команды
191. Function_1(); // вызываем подпрограмму "Funktion_1".
192. main();
193. break; // после возвращения из подпрограммы надо прервать выполнение конструкции "switch - case".
194.
195. case 2:
196. 
cout << "\nПоздравляем! Возможно, Вы выбрали цифру,да нет шучу я понимаю что вы нажали именно это: 2 \n";
197. Function_2();
198. main();
199. break;
200.
201. case 3:
202. cout << "\nТоже не плохо: 3 - вполне годная цифра,как говорили мне преподаватели иногда в школе \n";
203. Function_3();
204. main();
205. break;
206.
207. case 0:
208. cout << "\n Понравилась тыкать на кнопки,тогда всегда рады запускай еще \n\n";
209. // system("pause"); // напиши, и окно не закроется пока не нажмёшь любую клавишу
210. return 0; // возвращает значение в точку вызова функции. Возврат из основной функции означает окончание выполнения программы.
211. break;
212.
213.
214. default: // если не нашлось ни одного совпадения, то выполняем "действие по умолчанию".
215. cout << "\nВы невыйграли миллион,да что уж вы даже мимо нужных кнопок промохнулись! \n";
216. cout << "Можно выбрать только 1, 2 или 3 \n"; // выводим сообщение "защиты от дурака".
217. cout << "по теории если дать обезьяне печатную машинку и бесконечное число времени то она хоотично жмя на кнопки когданибудь напишет Гамлет,так что неунывай и пробуй еще";
218. cout << "\n";
219. main();
220. }
221. }
222.
223.
224.
225.
226. return 0;
227. }
