Иерархическая модель данных

Иерархическая модель данных является наиболее простой среди всех даталогических моделей. Исторически она появилась первой среди всех даталогических моделей: именно эту модель поддерживает первая из зарегистрированных промышленных СУБД IMS фирмы IBM.

Появление иерархической модели связано с тем, что в реальном мире очень многие связи соответствуют иерархии, когда один объект выступает как родительский, а с ним может быть связано множество подчиненных объектов. Иерархия проста и естественна в отображении взаимосвязи между классами объектов.

Основными информационными единицами в иерархической модели являются: база данных (БД), сегмент и поле. Поле данных определяется как минимальная, неделимая единица данных, доступная пользователю с помощью СУБД. Например, если в задачах требуется печатать в документах адрес клиента, но не требуется дополнительного анализа полного адреса, то есть города, улицы, дома, квартиры, то мы можем принять весь адрес за элемент данных, и он будет храниться полностью, а пользователь сможет получить его только как полную строку символов из БД.

Сегмент в терминологии Американской Ассоциации по базам данных DBTG (Data Base Task Group) называется записью, при этом в рамках иерархической модели определяются два понятия: тип сегмента или тип записи и экземпляр сегмента или экземпляр записи.

Тип сегмента — это поименованная совокупность типов элементов данных, в него входящих. Экземпляр сегмента образуется из конкретных значений полей или элементов данных, в него входящих. Каждый тип сегмента в рамках иерархической модели образует некоторый набор однородных записей. Для возможности различия отдельных записей в данном наборе каждый тип сегмента должен иметь ключ или набор ключевых атрибутов (полей, элементов данных). Ключом называется набор элементов данных, однозначно идентифицирующих экземпляр сегмента. Например, рассматривая тип сегмента, описывающий сотрудника организации, мы должны выделить те характеристики сотрудника, которые могут его однозначно идентифицировать в рамках БД предприятия. Если предположить, что на предприятии могут работать однофамильцы, то, вероятно, наиболее надежным будет идентифицировать сотрудника по его табельному номеру.

В иерархической модели сегменты объединяются в ориентированный древовидный граф. При этом полагают, что направленные ребра графа отражают иерархические связи между сегментами: каждому экземпляру сегмента, стоящему выше по иерархии и соединенному с данным типом сегмента, соответствует несколько (множество) экземпляров данного (подчиненного) типа сегмента. Тип сегмента, находящийся на более высоком уровне иерархии, называется логически исходным по отношению к типам сегментов, соединенным с данным направленными иерархическими ребрами, которые в свою очередь называются логически подчиненными по отношению к этому типу сегмента. Иногда исходные сегменты называют сегментами-предками, а подчиненные сегменты называют сегментами-потомками.

Рис. 1. Пример иерархических связей между сегментами

На концептуальном уровне определяется понятие схемы БД в терминологии иерархической модели.

Схема иерархической БД представляет собой совокупность отдельных деревьев, каждое дерево в рамках модели называется физической базой данных. Каждая физическая БД удовлетворяет следующим иерархическим ограничениям:

в каждой физической БД существует один корневой сегмент, то есть сегмент, у которого нет логически исходного (родительского) типа сегмента;
каждый логически исходный сегмент может быть связан с произвольным числом логически подчиненных сегментов;

каждый логически подчиненный сегмент может быть связан только с одним логически исходным (родительским) сегментом.

Между экземплярами сегментов также существуют иерархические связи. Рассмотрим, например, иерархический граф, представленный на рис. 2.

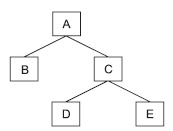
Рис. 2. Пример структуры иерархического дерева

Каждый тип сегмента может иметь множество соответствующих ему экземпляров.

Между экземплярами сегментов также существуют иерархические связи.

На рис. 3 представлены 2 экземпляра иерархического дерева соответствующей структуры.

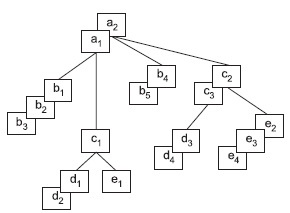
Рис. 3. Пример двух экземпляров данного дерева

Экземпляры-потомки одного типа, связанные с одним экземпляром сегмента-предка, называют "близнецами". Так, для нашего примера экземпляры b1, b2 и b3 являются "близнецами", но экземпляр b4 подчинен другому экземпляру родительского сегмента, и он не является "близнецом" по отношению к экземплярам b1, b2 и b3. Набор всех экземпляров сегментов, подчиненных одному экземпляру корневого сегмента, называется физической записью. Количество экземпляров-потомков может быть разным для разных экземпляров родительских сегментов, поэтому в общем случае физические записи имеют разную длину. Так, используя принцип линейной записи иерархических графов, пример на рис. 3 можно представить в виде двух записей:

а₁ b₁ b₂ b₃ c₁ d₁ d₂ e₁	a₂ b₄ b₅ c₂ c₃ d₃ d₄ e₂ e₃ e₄
Запись 1	Запись 2

Как видно из нашего примера, физические записи в иерархической модели различаются по длине и структуре.

Язык манипулирования данными в иерархической модели поддерживает в явном виде навигационные операции. Эти операции связаны с перемещением указателя, который определяет текущий экземпляр конкретного сегмента.

Сетевая модель данных

Базовыми объектами модели являются:

элемент данных;
агрегат данных;
запись;
набор данных.

Элемент данных — то же, что и в иерархической модели, то есть минимальная информационная единица, доступная пользователю с использованием СУБД.

Агрегат данных соответствует следующему уровню обобщения в модели. В модели определены агрегаты двух типов: агрегат типа вектор и агрегат типа повторяющаяся группа.

Агрегат данных имеет имя, и в системе допустимо обращение к агрегату по имени. Агрегат типа вектор соответствует линейному набору элементов данных. Например, агрегат Адрес может быть представлен следующим образом:

Адрес
Город	Улица	дом	квартира

Агрегат типа повторяющаяся группа соответствует совокупности векторов данных. Например, агрегат Зарплата соответствует типу повторяющаяся группа с числом повторений 12.

Зарплата
Месяц	Сумма
.	.

Записью называется совокупность агрегатов или элементов данных, моделирующая некоторый класс объектов реального мира. Понятие записи соответствует понятию "сегмент" в иерархической модели. Для записи, так же как и для сегмента, вводятся понятия типа записи и экземпляра записи.

Следующим базовым понятием в сетевой модели является понятие "Набор". Набором называется двухуровневый граф, связывающий отношением "один-ко-многим" два типа записи.

Рис. 4.

Набор фактически отражает иерархическую связь между двумя типами записей. Родительский тип записи в данном наборе называется владельцем набора, а дочерний тип записи — членом того же набора.

Для любых двух типов записей может быть задано любое количество наборов, которые их связывают. Фактически наличие подобных возможностей позволяет промоделировать отношение "многие-ко-многим" между двумя объектами реального мира, что выгодно отличает сетевую модель от иерархической. В рамках набора возможен последовательный просмотр экземпляров членов набора, связанных с одним экземпляром владельца набора.

Между двумя типами записей может быть определено любое количество наборов: например, можно построить два взаимосвязанных набора. Существенным ограничением набора является то, что один и тот же тип записи не может быть одновременно владельцем и членом набора.

В качестве примера рассмотрим таблицу, на основе которой организуем два набора и определим связь между ними:

Преподаватель	Группа	День недели	№ пары	Аудитория	Дисциплина
Иванов		Понедельник		22-13	КИД
Иванов		Понедельник		22-13	КИД
Карпова		Вторник		22-14	БЗ и ЭС
Карпова		Вторник		22-14	БЗ и ЭС
Карпова		Вторник		22-14	БД
Смирнов		Вторник		23-07	ГВП
Смирнов		Вторник		23-07	ГВП

Рис. 5.

Экземпляров набора Ведет занятия будет 3 (по числу преподавателей), экземпляров набора Занимается у будет 4 (по числу групп). На рис. 6 представлены взаимосвязи экземпляров данных наборов.

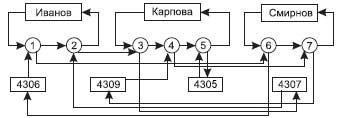
Рис. 6. Пример взаимосвязи экземпляров двух наборов

Среди всех наборов выделяют специальный тип набора, называемый "Сингулярным набором", владельцем которого формально определена вся система. Сингулярный набор изображается в виде входящей стрелки, которая имеет собственно имя набора и имя члена набора, но у которой не определен тип записи "Владелец набора". Например, сингулярный набор М.

Сингулярные наборы позволяют обеспечить доступ к экземплярам отдельных типов данных, поэтому если в задаче алгоритм обработки информации предполагает обеспечение произвольного доступа к некоторому типу записи, то для поддержки этой возможности необходимо ввести соответствующий сингулярный набор.

В общем случае сетевая база данных представляет совокупность взаимосвязанных наборов, которые образуют на концептуальном уровне некоторый граф.

Все операции манипулирования данными в сетевой модели делятся на навигационные операции и операции модификации.

Навигационные операции осуществляют перемещение по БД путем прохождения по связям, которые поддерживаются в схеме БД. В этом случае результатом является новый единичный объект, который получает статус текущего объекта.

Операции модификации осуществляют как добавление новых экземпляров отдельных типов записей, так и экземпляров новых наборов, удаление экземпляров записей и наборов, модификацию отдельных составляющих внутри конкретных экземпляров записей.

Реляционная модель данных

Теоретической основой этой модели стала теория отношений, основу которой заложили два логика — американец Чарльз Содерс Пирс (1839-1914) и немец Эрнст Шредер (1841-1902). В руководствах по теории отношений было показано, что множество отношений замкнуто относительно некоторых специальных операций, то есть образует вместе с этими операциями абстрактную алгебру. Это важнейшее свойство отношений было использовано в реляционной модели для разработки языка манипулирования данными, связанного с исходной алгеброй. Американский математик Э. Ф. Кодд в 1970 году впервые сформулировал основные понятия и ограничения реляционной модели, ограничив набор операций в ней семью основными и одной дополнительной операцией.

Основной структурой данных в модели является отношение, именно поэтому модель получила название реляционной (от английского relation — отношение).

N-арным отношением R называют подмножество декартова произведения D₁× D₂× … ×D_n множеств D₁, D₂, …, D_n (n > 1), необязательно различных. Исходные множества D₁, D₂, …, D_n называют в модели доменами.

R D₁ × D₂ × … × D_n

где D₁ × D₂ × … ×D_n— полное декартово произведение.

Полное декартово произведение — это набор всевозможных сочетаний из n элементов каждое, где каждый элемент берется из своего домена.

Например, имеем три домена: D₁ содержит три фамилии, D₂ — набор из двух учебных дисциплин и D₃ — набор из трех оценок. Допустим, содержимое доменов следующее:

D₁ = {Иванов, Крылов, Степанов};
D₂ = {Теория автоматов, Базы данных};
D₃ = {3, 4, 5}

Тогда полное декартово произведение содержит набор из 18 троек, где первый элемент — это одна из фамилий, второй — это название одной из учебных дисциплин, а третий — одна из оценок.

<Иванов,Теория автоматов,3>; <Иванов,Теория автоматов,4>; <Иванов,Теория автоматов,5> <Крылов,Теория автоматов,3>; <Крылов,Теория автоматов,4>; <Крылов,Теория автоматов,5>; …<Степанов,Базы данных,3>; <Степанов,Базы данных,4>; <Степанов,Базы данных,5>;

Отношение R моделирует реальную ситуацию и оно может содержать, допустим, только 5 строк, которые соответствуют результатам сессии (Крылов экзамен по "Базам данных" еще не сдавал):

<Иванов,Теория автоматов,4>; <Крылов,Теория автоматов,5>; <Степанов,Теория автоматов,5>; <Иванов,Базы данных,3>; <Степанов,Базы данных,4>;

Отношение имеет простую графическую интерпретацию, оно может быть представлено в виде таблицы, столбцы которой соответствуют вхождениям доменов в отношение, а строки — наборам из n значений, взятых из исходных доменов, которые расположены в строго определенном порядке в соответствии с заголовком. Такие наборы из n значений часто называют n-ками.

R
Фамилия	Дисциплина	Оценка
Иванов	Теория автоматов
Иванов	Базы данных
Крылов	Теория автоматов
Степанов	Теория автоматов
Степанов	Базы данных

Данная таблица обладает рядом специфических свойств:

В таблице нет двух одинаковых строк.
Таблица имеет столбцы, соответствующие атрибутам отношения.
Каждый атрибут в отношении имеет уникальное имя.
Порядок строк в таблице произвольный.

Вхождение домена в отношение принято называть атрибутом. Строки отношения называются кортежами.

Количество атрибутов в отношении называется степенью, или рангом, отношения.

Следует заметить, что в отношении не может быть одинаковых кортежей, что следует из математической модели: отношение — это подмножество декартова произведения, а в декартовом произведении все n-ки различны.

В соответствии со свойствами отношений два отношения, отличающиеся только порядком строк или порядком столбцов, будут интерпретироваться в рамках реляционной модели как одинаковые, то есть отношение R и отношение R₁, изображенное далее, одинаковы с точки зрения реляционной модели данных.

R1
Дисциплина	Фамилия	Оценка
Теория автоматов	Крылов
Теория автоматов	Степанов
Теория автоматов	Иванов
Базы данных	Иванов
Базы данных	Степанов

Любое отношение является динамической моделью некоторого реального объекта внешнего мира. Поэтому вводится понятие экземпляра отношения, которое отражает состояние данного объекта в текущий момент времени, и понятие схемы отношения, которая определяет структуру отношения.

Схемой отношения R называется перечень имен атрибутов данного отношения с указанием домена, к которому они относятся:

S_R = (A₁, A₂, A _n), A_i D_i.

Если атрибуты принимают значения из одного и того же домена, то они называются θ-сравнимыми, где θ — множество допустимых операций сравнения, заданных для данного домена. Например, если домен содержит числовые данные, то для него допустимы все операции сравнения, тогда θ = {=, <>,>=,<=,<,>} Однако и для доменов, содержащих символьные данные, могут быть заданы не только операции сравнения по равенству и неравенству значений. Если для данного домена задано лексикографическое упорядочение, то он имеет также полный спектр операций сравнения.

Схемы двух отношений называются эквивалентными, если они имеют одинаковую степень и возможно такое упорядочение имен атрибутов в схемах, что на одинаковых местах будут находиться сравнимые атрибуты, то есть атрибуты, принимающие значения из одного домена.

S_R1 = (A₁, A₂,..., A_n) — схема отношения R₁.

S_R2 = (B_i1, B_i2,..., B_in) — схема отношения R₂ после упорядочения имен атрибутов.

Тогда

Как уже говорилось ранее, реляционная модель представляет базу данных в виде множества взаимосвязанных отношений. В каждой связи одно отношение может выступать как основное, а другое отношение выступает в роли подчиненного. Это означает, что один кортеж основного отношения может быть связан с несколькими кортежами подчиненного отношения. Для поддержки этих связей оба отношения должны содержать наборы атрибутов, по которым они связаны. В основном отношении это первичный ключ отношения (PRIMARY KEY), который однозначно определяет кортеж основного отношения. В подчиненном отношении для моделирования связи должен присутствовать набор атрибутов, соответствующий первичному ключу основного отношения. Однако здесь этот набор атрибутов уже является вторичным ключом, то есть он определяет множество кортежей подчиненного отношения, которые связаны с единственным кортежем основного отношения. Данный набор атрибутов в подчиненном отношении принято называть внешним ключом (FOREIGN KEY).

Например, рассмотрим ситуацию, когда надо описать карьеру некоторого индивидуума. Каждый человек в своей трудовой деятельности сменяет несколько мест работы в разных организациях, где он работает в разных должностях. Тогда мы должны создать два отношения: одно для моделирования всех работающих людей, а другое для моделирования записей в их трудовых книжках, если для нас важно не только отследить переход работника из одной организации в другую, но и прохождение его по служебной лестнице в рамках одной организации (рис. 1).

Рис. 1. Связь между основным и подчиненным отношениями

PRIMARY KEY отношения Сотрудник атрибут Паспорт является FOREIGN KEY для отношения "карьера".