Ряды Фурье
Периодические функции
Колебательные и вращательные движения деталей машин, акустические и электромагнитные колебания – примеры периодических процессов, математически описываемых периодическими функциями.
Определение. Функция 
называется периодической, если существует число 
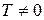такое, что для любого 
выполняется равенство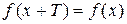 
. Число 
называется периодом функции .
Некоторые основные свойства периодических функций:
1. Если – период функции, то каждое число вида nТ, где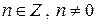 
, также является периодом этой функции.
2. Сумма, разность, произведение, частное функций с периодом являются периодическими функциями с периодом .
3. Для постоянной функции любое число является периодом.
4. Если – интегрируемая периодическая функция с периодом , то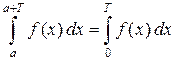 
при любом 
, т.е. интеграл по любому отрезку длины имеет одно и то же значение.
Обычно периодом функции называют её наименьший положительный период.
Непериодическую функцию , заданную на некотором отрезке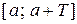 
длины , можно доопределить периодически на всю числовую ось, построив её периодическое продолжение – функцию 
с периодом , совпадающую с на интервале 
. При этом на концах интервала может не совпадать с .
В математике простейшие периодические функции – это тригонометрические функции 
и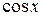 
, период которых равен 
.
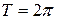В физике простейшей периодической функцией считается гармоническое колебание («гармоника»)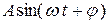 
(
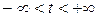), где 
– амплитуда колебания,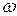 
– круговая частота, 
– начальная фаза. Величина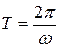 
является периодом гармоники.
Тригонометрический ряд Фурье
Рассмотрим бесконечную последовательность гармоник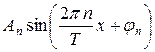 
, 
, 
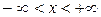, дополнив её постоянной 
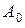. При число 
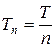является периодом n -ой гармоники, поэтому по свойствам 1 и 3 величина , будучи кратной всем 
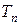, является общим периодом всех гармоник последовательности, в том числе и .
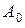Составим из последовательности гармоник функциональный ряд. Если он сходится, то его сумма будет периодической функцией с периодом . Для всех обозначим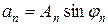 
, 
и, положив 
, 
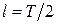, преобразуем гармоники: 
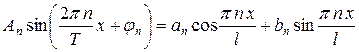. Запишем разложение функции в ряд:
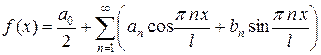. (1)
Ряд в правой части равенства (1) называется тригонометрическим рядом, а само равенство называется разложением функции в тригонометрический ряд. Оно даёт представление определяемого функцией периодического колебания в виде бесконечного ряда («бесконечной суммы») гармонических колебаний.
Пусть тригонометрический ряд (1) равномерно сходится к своей сумме на отрезке 
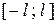, длина которого равна периоду 
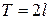. Интегрируя разложение (1) почленно на отрезке 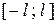, получаем:
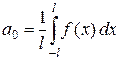. (2)
Умножая обе части равенства (1) на интегрируемые функции
и интегрируя почленно, точно так же получаем:
(
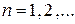), (3)
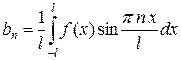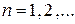(). (4)
Определение. Коэффициенты разложения (1), определяемые по формулам (2) – (4), называются коэффициентами Фурье функции , а тригонометрический ряд с такими коэффициентами называется рядом Фурье функции .
Частные случаи:
1. Если является чётной функцией на 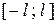, то произведения 
являются чётными, а 
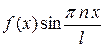– нечётными, и по свойству определённого интеграла формулы (2) – (4) дают
, 
, 
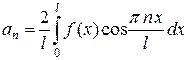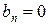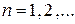(), (5)
вследствие чего ряд Фурье чётной функции имеет вид
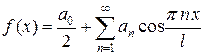, (6)
называемый рядом Фурье по косинусам.
2. Если – нечётная на 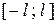функция, то
, 
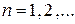, (), (7)
и ряд Фурье имеет вид ряда Фурье по синусам:
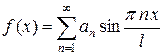. (8)
Вопрос. Какими свойствами должна обладать функция , чтобы построенный для неё тригонометрический ряд Фурье сходился, и его сумма совпадала с в требуемых точках?
Определение. Функция называется кусочно-монотонной на отрезке 
, если его можно разбить точками на конечное число интервалов так, что на каждом из них функция будет монотонной, то есть либо возрастающей, либо убывающей (см. рис.).
Кусочно-монотонная и ограниченная на отрезке функция может иметь на нём разрывы только первого рода.
Теорема (Дирихле). Если периодическая функция с периодом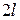 
является кусочно-монотонной и ограниченной на отрезке 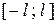, то её тригонометрический ряд Фурье сходится во всех точках, и для его суммы 
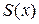выполняются равенства:
а)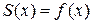 
в точках непрерывности ;
б)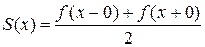 
в точках разрыва , где 
и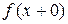 
– пределы соответственно слева и справа в точке .
