Эллипс. Каноническое уравнение эллипса. Его свойства. Форма. Эксцентриситет. Фокальный параметр. Фокальные радиусы. Параметрические уравнения эллипса. Построение точек эллипса.
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Обозначим фокусы через F1 и F2, расстояние между ними через 2c, а сумму расстояний от произвольной точки эллипса до фокусов — через 2a (см. рис. 49). По определению 2a > 2c, т. е. a > c.
Для вывода уравнения эллипса выберем систему координат так, чтобы фокусы F1 и F2 лежали на оси, а начало координат совпадало с серединой отрезка F1F2. Тогда фокусы будут иметь следующие координаты: F1(-c.0) F2(c.0).
Пусть М(х,у) произвольная точка. Тогда согласно определению эллипса МF1+MF2=2a то есть 
(11,5) Это, по сути, и есть уравнение эллипса. Преобразуем уравнение (11.5) к более простому виду следующим образом:
Так как a>с, то а*a-с*c>0. Положим 
(11.6)
Тогда последнее уравнение примет вид 
или каноническим уравнением эллипса.
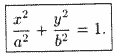
Задание прямой на плоскости, уравнения прямой на плоскости.
Опр.Вектор параллельный данной прямой наз. направляющим вектором этой прямой. Рассмотрим задание прямой точкой и направляющим вектором R 
-аффинный, 
(
)-направляющий вектор,т.М(
)-произвольная точка.М(х,у)
1) 
=t ,t-число 
R-векторное уравнение прямой
2) 
(х- 
,у- 
),t (t 
-t 
)
Тогда х- = t ; х= + t ; Параметрическое уравнение
у- = t ; у= + t ;
3)Если прямая d не параллельна ни одной из координат осей, то 
0, 
0, тогда уравнение примет вид 
= 
-каноническое уравнение прямой на плоскости
4) 
=0; (
)- 
(
)=0; х- у+(- 
+ 
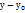)=0
Ах+Ву+С=0- уравнение прямой
Покажем, что любое линейное ур-ние с двумя переменными на плоскости задаёт прямую:
Ах+Ву+С=0, 
+ 
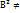0,Пусть А 
0, х+ 
+ 
=0, 
=0, М(- 
;0), (-В;А) || 
(- 
;1)
Вывод: Из рассуждений можно сделать вывод Ах+Ву+С=0, есть ур-ние прямой проходящей через т.М(- ;0) и направляющим вектором, который (-В;А).Уравнение Ах+Ву+С=0-наз. общим уравнением прямой на плоскости.
5)Пусть заданы точки 
(, 
) и 
(
, 
) прямой d, не параллельной ни одной из координатных осей.Тогда ( - , - )-направляющий вектор этой прямой и 
= 
-есть ур-ние прямой d.
6)Пусть прямая пересекает оси координат.А(а;0),В(0;b), М(х;у).АВ-прямая.Пусть есть т.А(а;0) и направляющий вектор 
(-а; b). Т.М(х;у)-произвольная точка заданной прямой.
Каноническое уравнение:
= 
; 
+ 
- =0, 
- =-1, 
+ =1 – ур-ние прямой в отрезках.
7)Ур-ние прямой с угловым коэффициентом
Рассмотрим прямую, которая не параллельна оси Оу.
d 
,Пусть 
, 
-направляющие векторы прямой d. (
, 
), (
, 
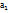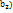, || ,координаты этих векторов пропорцианальны; =λ 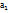, =λ , 
=λ , 
= 
=k,Отношение второй координаты к первой у всех направляющих векторов прямой d, есть величина постоянная(обозн.,k)и наз. угловым коэффициентом. Выведем уравнение прямой: Пусть прямая пересекает ось Оу в точке В(0;b).т.М имеет координаты(х;у), произвольная точка прямой. 
(х;у- b), 
=k, y-b=kx; y=kx+b, y=kx+b-ур-ние с угловым коэффициентом.
Прямая как линия пересечения двух плоскостей.
+ 
+ 
=0 
+ 
+ 
=0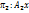
0 или 
или 
0 - одно из условий(
Запишем каноническое и параметрическое ур-нии такой прямой.
Найдём т. 
и направляющий вектор. 
, 
.
Выполним следующие алгебраические преоразования.
+ 
+ =0 
+ 
+ =0
+ + 
- 
+ + )=0
+ + )- 
+ + ) =0
=u, 
= v, 
(
uv= 
v:w= 
u:v= 
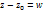
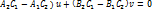
v:w= u:v:w= 
т.к. 
, 
, 
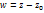
Рассмотрим т.M(x,y,z) И т. (
=(
-x, 
-y, 
-z) Тогда с точностью до коллинеарности, можно сказать, что направляющий вектор для данной прямой будет:
(
), тогда параметрическое ур-ние прямой:
x= + 
y= 
z= 
Каноническое ур-ние прямой:
= 
