Метод середнього арифметичного

Частина 2

ІІ Семестр

 

Київ 2010

Затверджено на засіданні кафедри фізики

Державного університету інформаційно-комунікаційних технологій як

методичні вказівки до виконання лабораторних робіт з курсу фізики

ІІ семестру

(протокол № ___ від _______________р.)

Завідувач кафедрою фізики___________Л.М. Гориня

Зміст

 

1. Обробка результатів вимірювань при виконанні лабораторних робіт ………………..4

2. Лабораторна робота №12.Вивчення термоелектрорушійної сили…………………….11

3. Лабораторна робота №13.Вивчення температурної залежності електричного опору металів………………………………………………………………………………………16

4. Лабораторна робота №14 Вивчення температурної залежності електричного опору напівпровідників………………………… ………………………………………………..24

5. Лабораторна робота №15Визначення концентрації вільних носіїв заряду в напівпровіднику………………………… ………………………………………………..34

 

Обробка результатів вимірювань при виконанні лабораторних робіт з курсу «Фізика»

Вимірювання фізичних величин є метою кожної лабораторної роботи з фізики. Вимірювання – це процес порівняння фізичної величини з іншою, якає є однорідною з нею, і яка прийнята за одиницю вимірювання. При цьому розрізняють прямі та непрямі вимірювання.

Виміряти фізичну величину (ФВ) – це значить знайти дослідним шляхом значення фізичної величини, використовуючи технічні засоби. Вимірювання поділяються на прямі та непрямі. Прямі вимірювання отримуються шляхом безпосерднього спостереження за мірою або приладом. Непрямі вимірювання отримуюмуються шляхом розв’язування рівнянь.

Результати вимірювань ФВ, наприклад, в лабораторії завжди є не абсолютно точними, а наближеними. Точність вимірювань залежить від багатьох факторів. Мірою точності вимірювань є похибка. Похибки вимірювань можна класифікувати по-різному. Наприклад: похибки методу вимірювань, інструментальні похибки, похибки через зовнішні впливи на засоби і об’єкти вимірювань, похибки відліку, суб’єктивні похибки. В основному похибка складається з інструментальної похибки та похибки відліку.

Похибки поділяються також на абсолютні та відносні.

Абсолютна похибка ФВ х - це іменоване число, яке показує межі вимірюваної ФВ.

Абсолютна похибка визначається різницею між істинним та наближеним значеннями вимірюваної ФВ.

Відносна похибка – це відношення абсолютної похибки вимірювання до істинного значення вимірюваної величини. Відносна похибка вимірюється у відсотках, використовується для порівняння якості вимірювань різнорідних величин.

Існують різні методи визначення величин похибок.

 

Метод середнього арифметичного

Метод середнього арифметичного застосовується при прямих вимірюваннях, коли похибка вимірювального приладу менша похибки відліку.

Найбільше до істинного значення вимірюваної ФВ наближається її середнє арифметичне значення. Нехай маємо n прямих вимірювань ФВ х:

 

.

 

1. Визначається середнє арифметичне ФВ х

 

(1)

Примітка. При кінцевому числі n величина називається виборочним середнім або середнім вибірки.

2. Визначається абсолютна похибка кожного вимірювання

 

 

3. Обчислюється середня абсолютна похибка

 

(2)

 

4. Обчислюється відносна похибка

 

(3)

 

Якщо в процесі багатократних вимірювань вимірювальний прилад дає однакові покази, то за максимальну абсолютну похибку приймають похибку вимірювального приладу або ціну поділки шкали приладу.

5. Записується результат вимірювання

 

(4)

 

Статистичний метод

Похибки також поділяються на систематичні, випадкові, промахи. Систематичні похибки та промахи можна звести до мінімального значення, наприклад до нуля. Випадкові похибки - це похибки, які в однакових умовах мають різні значення. Випадкові похибки не можна звести до нуля, можна лише зменшити їхню величину шляхом збільшення кількості вимірювань в ідентичних умовах. Випадкові похибки досліджуються в теорії імовірностей. Похибки відліку при зніманні показів мір або вимірювальних приладів оком людини також можна обробляти статистичним методом.

 

Закон нормального розподілу випадкових похибок та статистична обробка при нормальному розподілі результатів спостережень

Нехай маємо n (100) вимірювань ФВ х( ). Обчислимо середнє арифметичне ФВ х - і знайдемо абсолютні похибки . Розглянемо величини цих випадкових похибок і розділимо їх на певні інтервали, враховуючи їхній знак. Побудуємо гістограму. Для цього по осі ОХ відкладатимемо величини похибок, а по осі ОY кількість похибок які потрапляють в цей інтервал.

 

 

Якщо кількість вимірювань збільшувати (), а величину інтервалу зменшувати, то гістограма наближатимеся до плавної кривої, яка має форму кривої Гаусса (нормальний розподіл Гаусса або розподіл густини імовірностей). Аналітичний вигляд кривої Гаусса є

 

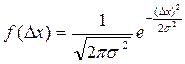(5)

 

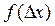– густина імовірності. Вона дозволяє визначити імовірність dP появи випадкової похибки в інтервалі похибок d(Δx) за формулою

 

,

 

а імовірність появи випадкової похибки в кінцевому інтервалі значень [Δ x ₁, Δ x ₂] буде дорівнювати

 

(6)

 

 

Δ x - абсолютна випадкова похибка результату спостереження, коли систематична похибка повністю виключена, параметр σ називається дисперсією і характеризує розкид значень випадкової похибки відносно нульового значення. Квадратний корінь з дисперсії називається середньо квадратичним відхиленням (середньо квадратичною похибкою). Параметр σ зручно використовувати для оцінки якості проведених спостережень. Так, якщо його значення взяти в якості границь випадкової похибки результату спостереження, то за формулою (6) імовірність Р₁ того, що похибка результату спостереження перебуває в межах [- σ, + σ ], дорівнює

 

(7)

 

Аналогічно можна отримати імовірність появи похибки реультату спостереження в межах інтервалу [-2 σ, +2 σ ] – вона дорівнює 0,95, а в межах інтервалу [-3 σ, +3 σ ] – 0,99. Це означає, що з серії спостережень, кількість яких прийнято за 100%, для 68% з них випадкова похибка не вийде за межі , у 95% - за межі 95 % 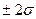, а для 99% - за межі . Тобто, параметр σ дозволяє визначити границі інтервалу випадкової похибки з деякою імовірністю. Середньо квадратичну похибку називають ще стандартною похибкою. Середньо квадратична стандартна похибка визначається за формулою

 

(8)

 

Формула (8) дає дещо занижене значення дисперсії, бо відрізняється від істинного значення вимірюваної величини, тому оцінка середньо квадратичної (стандартної) похибки проводиться на основі дослідних даних за формулою

 

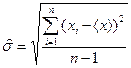(9)

 

Верхня та нижня границі інтервалу, що покриває з заданою імовірністю похибку вимірювання, називаються довірчими границями похибки, інтервал – довірчим, а імовірність, що його характеризує – довірчою імовірністю. Границі довірчого інтервалу визначаються за формулою

 

(10)

 

Для довірчого інтервалу 68% 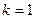(для значень є таблиці).

Таким чином, результатом вимірювання ФВ є середнє арифметичне результатів спостережень та довірчий інтервал випадкової похибки.

При кінцевій кількості спостережень (вимірювань) розподіл Гаусса застосовується з певним ступенем наближення. В цьому випадку для визначення границь довірчого інтервалу замість формули (10) в якій коефіцієнт залежить тільки від імовірності Р, використовується інша формула

 

(11)

 

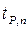- коефіцієнт Стьюдента, який залежить не тільки від імовірності Р, але й від кількості спостережень n в серії, його беруть з таблиці.

 

p n	0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,999
	1,00	1,38	2,0	3,1	6,3	12,7	31,8	636,6
	0,82	1,06	1,3	1,9	2,9	4,3	7,0	31,6
	0,77	0,98	1,3	1,6	2,4	3,2	4,5	12,9
	0,74	0,94	1,2	1,5	2,1	2,8	3,7	8,6
	0,73	0,92	1,2	1,5	2,0	2,6	3,4	6,9
	0,72	0,90	1,1	1,4	1,9	2,4	3,1	6,0
	0,71	0,90	1,1	1,4	1,9	2,4	3,0	5,4
	0,71	0,90	1,1	1,4	1,9	2,3	2,9	5,0
	0,70	0,88	1,1	1,4	1,8	2,3	2,8	4,8
∞	0,67	0,84	1,0	1,3	1,6	2,0	2,3	3,3

 

Середньо квадратична похибка результату при кінцевій кількості спостережень (вимірювань) оцінюється за формулою

 

(12)

 

Обробка результатів непрямих вимірювань

При непрямих вимірюваннях фізичної величини а її значення визначається за функціональною залежністю між нею та величинами аргументів, значення яких знайдене в результаті прямих вимірювань, тобто . Метод оцінки величини a та похибки її вимірювання наступні. Для простоти розглянемо простий випадок, коли величини a є функцією одного аргументу:

 

(13)

Розглянемо цю функцію поблизу в межах інтервалу , де - оцінка величини х, а - похибка її вимірювання. Розкладемо функцію в ряд Тейлора, тобто представимо її у вигляді багаточлена:

 

, (14)

 

де - похідна n – го порядку в точці 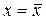. Враховуючи, що похибка вимірювання величини х є малою величиною, зберігають лише члени першого порядку. Тоді:

 

(15)

 

Доданок із (15) є оцінкою значення величини а, тобто

 

,

 

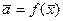де - визначається з формулою

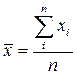(16)

Другий доданок в (15) визначає похибку вимірювання величини а

 

, (17)

 

де . Враховуючи, що похибка величини х може бути як із знаком “+”, так і з “-“, рівняння (17) записують у вигляді

 

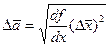(18)

 

У загальному випадку , де , де і =1, 2,…, к

Якщо похибки вимірювання величини 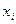мають лише випадковий характер, то абсолютна похибка вимірювання величини а визначається за формулою

 

,

де - частинні похідні при , а - похибки вимірювання величини .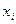

Результат непрямого вимірювання представляється у вигляді

 

 

Якщо вимірювана величина є функцією кількох змінних, похибки яких порівняно невеликі, то похибка непрямого вимірювання може бути визначена на основі формул таблиці. При цьому розраховують стандартну похибку з довірчим інтервалом та довірчою імовірністю 68%.

 

 

Лабораторна робота № 12

 

Вивчення термоелектрорушійної сили

 

Мета роботи.

Знайти залежність термоелектрорушійної сили (термо-е.р.с.) від різниці температур металевих контактів, визначити коефіцієнт термо-е.р.с. та співвідношення концентрацій електронів провідності в металах, що дотикаються.

 

2. Теоретичні відомості.

В металі вільні електрони переміщуються по кристалу, а найшвидші з них можуть відділятись від зовнішнього шару позитивних іонів гратки і вийти з кристала.

В тих місцях, які залишили електрони, виникає надлишковий позитивний заряд, який примушує ті електрони, у яких швидкість не дуже велика, повернутися назад. Окремі електрони будуть увесь час залишати метал, віддалятись від нього на декілька атомних відстаней і повертатися назад.

Внаслідок цього біля поверхні металу буде весь час існувати подвійний електричний шар, який складається з електронної хмари за межами металу та позитивно заряджених іонів гратки. Цей шар немов би виконує роль конденсатора, електричне поле якого перешкоджає вивільненню нових електронів з середини металу назовні.

Для того, щоб електрон міг залишити метал, він повинен мати енергію, достатню для виконання роботи з подолання потенціального бар’єру з боку подвійного електричного шару.

Найменша енергія, яку потрібно надати електрону для вивільнення його з речовини, називається роботою виходу електрона. Робота виходу А чисельно дорівнює мінімальній зміні енергії системи електрон-метал при видаленні з неї електрона:

 

, (1)

 

де е =1,6·10^-19 Кл – елементарний заряд, 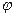- потенціал виходу.

Робота виходу та потенціал виходу для різних металів є різними, а для одного і того ж металу суттєво залежать від чистоти та стану його поверхні.

При дотику двох металів, що мають різні роботи виходу, електрони переходять із металу з меншою роботою виходу, у метал із більшою роботою виходу, тобто з більш високих енергетичних рівнів в першому металі на більш низькі рівні в другому.

Цей перехід триває доти, доки рівні Фермі в обох металах зрівняються і встановиться деяка динамічна рівновага.

Внаслідок цього потенціал виходу в першому металі зменшиться, а в другому збільшиться, і між поверхнями металів виникає стрибок потенціалу. Він називається зовнішньою контактною різницею потенціалів і обчислюється за формулою:

 

, (2)

 

Зовнішня контактна різниця потенціалів визначається потенціалами виходу або роботами виходу металів контакту.

Контактна різниця потенціалів виникає не тільки між двома металами, але й між двома напівпровідниками, що контактують.

Контакт, тобто щільне дотикання двох тіл, можна створити, якщо відшліфувати їхні поверхні, забезпечивши відсутність зовнішніх включень.

Італійський науковець Вольт в 1801-1802 роках встановив два закони:

1) при дотику двох металів між ними виникає контактна різниця потенціалів, величина якої залежить від роду металів та їхньої температури;

2) різниця потенціалів між кінцями послідовно сполучених контактів різнорідних металів при однаковій температурі не залежить від роду проміжних контактів і визначається тільки крайніми елементами цього з'єднання.

З цих законів випливає, що в замкнутому полі з двох різнорідних металів (термопара) при однаковій температурі контактів струм буде відсутній, оскільки не буде різниці потенціалів. Якщо ж температури контактів Т₁ і Т₂, будуть різними, то виникне різниця потенціалів ε₁, величина якої визначається за формулою:

 

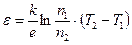(3)

 

і яка називається термоелектрорушійною силою або термо-е.р.с.

В колі термопари при цьому буде існувати електричний струм. Величина

 

(4)

називається коефіцієнтом термо-е.р.с. і залежить від концентрації електронів n₁ і n₂ в металах, що дотикаються. Для різних пар металів коефіцієнт термоерс має різні значення. З врахуванням виразу (4) формулу (3) можна записати так:

 

, (5)

 

де ∆Т=Т₂-Т₁ — різниця температур спаїв.

Отже, величина термо-е.р.с. ε прямопропорційно залежить від різниці температур спаїв ΔТ, а також від природи металів контакту.

На величину термоерс впливають також дифузійні переходи електронів з одного металу до іншого внаслідок градієнту температур вздовж провідника при нагріванні одного з контактів.

З формули (5) випливає, що

 

, (6)

 

тобто коефіцієнт термоерс чисельно дорівнює термоелектрорушійній силі, що виникає при різниці температур спаїв в 1К.

Вимірюється коефіцієнт термоерс в В/К; мВ/К і мкВ/К.

 

3. Контрольні запитання.

1. Що називається роботою виходу електрона?

2. Від чого залежить робота виходу?

3. Як обчислюється зовнішня контактна різниця потенціалів?

4. Чим визначається внутрішня контактна різниця потенціалів?

5. В чому полягає явище виникнення термо-е.р.с.?

6. Від чого залежить величина термо-е.р.с.?

7. Що показує і від чого залежить коефіцієнт термо-е.р.с.?

8. Як вимірюється величина термо-е.р.с. в даній лабораторній роботі?

9. Чому при даному методі вимірювання проводити вимірювання потрібно швидко, а нагрівати повільно?

10. Як в даній лабораторній роботі визначається коефіцієнт термо-е.р.с.?

11. Яка конструкція термопари?

 

4. Домашнє завдання.

Для виконання роботи необхідно засвоїти такі питання: контактна різниця потенціалів; потенціал виходу і робота виходу; закон Вольта; термоелектрика; термопари.

 

Лабораторне завдання.

Установка складається з термопари, один із спаїв якої знаходиться в нагрівнику (саме цей спай протягом виконання лабораторної роботи буде нагріватись), а інший – на відкритому повітрі (його температура буде залишатись постійною протягом усього експерименту і дорівнюватиме кімнатній). До першого спаю під’єднана інша термопара, яка з’єднана з цифровим термометром, роль якого відіграє мультиметр. При пропусканні струму через нагрівник один зі спаїв досліджуваної термопари нагрівається.

Величина струму в нагрівнику регулюється реостатом і контролюється амперметром. Струм в колі термопари, яка досліджується, вимірюється мікроамперметром. Якщо нагрівання відбувається повільно, то при одній і тій же різниці температур спаїв термострум можна виміряти двічі: один раз без опору R, другий раз з опором R (рис. 1).

У першому випадку струм визначається величиною термоерс та загальним опором кола R₀:

 

(7)

 

В другому випадку струм буде меншим, бо в коло вмикається додатковий опір R. Тоді для струму буде справедливий вираз:

 

(8)

 

Розв'язок системи рівнянь (7) і (8) для термоерс буде:

 

(9)

 

Вимірювання термо-е.р.с. за цим способом треба здійснювати настільки швидко, щоб різниця температур спаїв не встигала помітно змінитись за час вимірювання.

 

Порядок виконання роботи.

1. Зібрати вимірювальну схему за рис. 1.

 

 

Рис. 1.

2. Визначити кімнатну температуру (ця температура буде рівна температурі холодного контакту t₁).

3. Увімкнути нагрівач через автотрансформатор і за допомогою реостата встановити в ньому струм не більше 0,5 А.

4. Поступово нагрівати один зі спаїв, визначаючи температуру холодного t₁, і гарячого t₂ спаїв за термометрами.

5. Через кожні 10º С різниці температур спаїв виміряти в колі термопари струми І₁ і І₂ (з опором R і без нього).

6. Результати вимірювань записати до таблиці 1.

 

Таблиця 1. Результати вимірювань.

t1, o C
t2, o C
І1, мкА
І2, мкА

 

 

 

6. Для кожної різниці температур Δ t спаїв обчислити за формулою (9) величину термо-е.р.с. ε і результати обчислень занести до таблиці 2.

 

Таблиця 2. Результати розрахунків.

t,o C
ε, мкВ

 

7. Побудувати графік залежності термо-е.р.с. ε від різниці температур спаїв ∆t в координатах ε та t.

8. Визначити величину коефіцієнта термо-е.р.с. як тангенс кута нахилу залежності E= f (t) згідно з формулою (6).

9. Знайти співвідношення концентрацій носіїв n₁ і n₂ в металах, що дотикаються, використавши для цього формулу (3), відповідним чином її перетворивши.

 

6. Прилади та обладнання.

Термопари, мікроамперметр, мультиметри, нагрівач, амперметр, автотрансформатор, реостат.

 

7. Література.

1. Савельев И. В. Курс общей физики, т.ІІ. М., “Наука”, 1982, 77,78.

2. Зисман Г. А., Тодес О. М. Курс общей физики, т.ІІ. М., “Наука”, 1969, 22.

Лабораторна робота №13

 

Вивчення температурної залежності електричного опору металів

 

1. Мета роботи.

Знайти залежність електричного опору металу від температури, визначити величину опору металевого провідника при температурі 0°С і величину температурного коефіцієнта опору.

 

2. Теоретичні відомості.

Електричні властивості кристалічних твердих тіл визначаються будовою їх кристалічної ґратки і характером сил, які діють між частинками твердого тіла, тобто типом хімічного зв'язку.

В залежності від того, які частинки перебувають у вузлах кристалічної ґратки та яка природа сил взаємодії між ними, розрізняють такі основні типи кристалів: іонні, атомні, металічні та молекулярні.

У вузлах ґратки іонних кристалів розміщуються іони різних знаків, сили взаємодії між якими переважно є електростатичними. Прикладом є гратка кам'яної солі NaCl, при створенні якої натрій віддає свій єдиний валентний електрон хлорові, якому не вистачає одного електрона для заповнення валентної оболонки (рис. 1).

 

 

 

Рис 1. Рис. 2.

 

Внаслідок цього обидва атоми стають іонами протилежних знаків та набувають стійких зовнішніх оболонок. Відсутність вільних носіїв заряду пояснює низьку електропровідність іонних кристалів.

У більшості випадків такі кристали є ізоляторами.

У вузлах ґратки атомних кристалів розташовані нейтральні атоми, зв'язок між якими здійснюється шляхом створення спільної пари валентних електронів (по одному електрону від кожного атома) і називається ковалентним. Такий зв'язок має місце, наприклад, між атомами в молекулі водню. При зближенні двох атомів водню траєкторії їхніх електронів перекриваються (рис. 2).

В області перекриття електрони перебувають під дією сильного притягання з боку обох ядер і починають рухатись по складним орбітам навколо обох ядер, тобто атоми виявляються зв'язаними спільною парою електронів.

При цьому виникає так звана обмінна взаємодія, вона лежить в основі ковалентного зв'язку і має квантову природу. Не зважаючи на те, що енергія зв'язку в атомних кристалах є значною, в багатьох з них можливе вивільнення електронів з ковалентних зв'язків. Під дією електричного поля вивільнені електрони стають носіями струму. Чим вища температура кристалу, тим більше виникає електронів провідності. Багато з таких кристалів (елементи з середньої групи таблиці Менделєєва, наприклад, германій та кремній і різні сполуки) є напівпровідниками.

У вузлах гратки металічних кристалів розташовані позитивні іони, між якими рухаються електрони. Вони створюють так званий електронний газ, який рівномірно заповнює простір між іонами. Цей тип гратки характерний для елементів (металів), у яких валентні електрони слабко зв'язані з ядром. При виникненні кристалічної гратки ці електрони легко відокремлюються від атомів і стають спільними для всього кристала.

Електронний газ зв'язує в міцну систему позитивно заряджені іони кристалу. Під впливом сил притягання з боку електронного газу і сил відштовхування між іонами останні розташовуються на деякій рівноважній відстані один від одного. Ця відстань відповідає мінімуму енергії в кристалі. Тіла з такою кристалічною граткою відзначаються високою електропровідністю, оскільки навіть слабке електричне поле викликає переміщення вільних електронів. При підвищені температури кристалу збільшується інтенсивність теплового коливального руху іонів, що затруднює напрямлений рух електронів в електричному полі.

У вузлах ґратки молекулярних кристалів знаходяться нейтральні молекули. Вони утримуються вандерваальсівськими силами, природа яких визначається взаємодією молекулярних диполів. За звичайних умов такі кристали електропровідністю не володіють і при підвищенні температури легко руйнуються. Молекулярну кристалічну гратку мають більшість органічних сполук.

Згідно з квантовою теорією енергія електронів в атомах квантується, тобто може приймати лише дискретні значення. Ці значення енергії відповідають енергетичним рівням. Якщо однакові атоми ізольовані один від одного, то вони мають однакові енергетичні рівні. При виникненні кристала відбувається зміна енергетичних рівнів у зв'язку із взаємодією атомів між собою. Якщо кристал складається з N атомів, то замість одного однакового для всіх атомів рівня виникає N дуже близьких за значеннями енергії рівнів, які не співпадають між собою. Так відбувається розщеплення енергетичного рівня на низку енергетичних рівнів.

Сукупність цих рівнів називається зоною енергетичних рівнів. Розщеплення енергетичних рівнів і виникнення зони енергетичних рівнів, яке має місце при зближенні атомів і виникненні кристала, здійснюється згідно з принципом Паулі, за яким на одному енергетичному рівні може перебувати не більше двох електронів з різною орієнтацією спінів.

Сукупність значень енергій, які можуть мати електрони в даному атомі (зони дозволених енергій) чергуються зі значеннями енергій, які електрони в даному атомі мати не можуть (зони заборонених енергій).

Ступінь розщеплення для різних рівнів неоднаковий. Рівні, заповнені близькими до ядра внутрішніми електронами, розщеплюються незначно, оскільки ці електрони слабко взаємодіють з електронами і ядрами інших атомів кристала. Така взаємодія є значною для валентних електронів, внаслідок чого їхні рівні розщеплюються сильніше, утворюючи так звану валентну зону. Ще помітнішим є розщеплення більш високих, ніж валентні, енергетичних рівнів, не зайнятих електронами в основному стані атома.

У кристалів різних типів ступінь заповнення валентної зони електронами різний, тому енергетичні зони розташовані по-різному, чим пояснюється різна за величиною їхня електропровідність.

При абсолютному нулі температури енергія кристала мінімальна, що відповідає заповненню електронами валентної зони, починаючи з найбільш низьких її рівнів. При підвищенні температури енергія теплового руху електронів зростає і вони стають здатними займати більш високі енергетичні рівні.

Якщо створити вкристалі електричне поле, то воно може спричинити скероване переміщення цих електронів (електрострум провідності). Однак це можливо лише в таких кристалах, де є більш високі енергетичні рівні, які можуть бути заповненими електронами. Сукупність таких рівнів називається зоною провідності.

В металічних кристалах кількість валентних електронів менша від кількості енергетичних рівнів, на які ці електрони можуть переходити. Наприклад, у одновалентних металів валентна зона заповнена наполовину, а незаповнена її частина є зоною провідності (рис. 3).

 

Рис. 3.

У двовалентних металів валентна зона заповнена повністю, проте верхня її зона виявляється розташованою вище від нижньої границі наступної зони дозволених енергій (рис. 4), тобто ці зони частково перекриваються і область перекриття стає зоною провідності. Такі кристали є провідниками електричного струму.

 

 

Рис. 4.

 

Температурна залежність електропровідності будь-якого матеріалу визначається залежністю від температури концентрації носіїв струму та їхньою рухливістю. В металах концентрація електронів провідності незмінна, а рухливість електронів з підвищенням температури зменшується, отже зменшується провідність і збільшується опір кристалів.

Класична теорія провідності металів грунтується на тому, що вільні електрони (електронний газ) поводять себе так, як молекули ідеального газу. Вони рухаються зі швидкістю , співударяються переважно зіонами гратки, пробігаючи між зіткненнями відстань , яка називається середньою довжиною вільного пробігу і дорівнює значенню міжатомної відстані в кристалі. На основі цих уявлень, можна отримати наступний вираз для питомої електропровідності металів:

 

(1)

 

де n - концентрація електронів, е - заряд електрона, m - маса електрона.

В цьому виразі величини n, m, е, λ- сталі, а прямопропорційна до , де Т - температура. Таким чином, за класичною теорією питома електропровідність залежить від природи металу і обернено пропорційна .

Однак, досліди показують, що в широкому інтервалі температур опір металів прямопропорційний до Т (рис. 5).

 

 

 

Рис. 5.

 

В інтервалі середніх і високих температур опір металів збільшується при зростанні температури за лінійним законом

 

, (2)

 

де R і R₀ - опір при температурах t°С і 0° С відповідно, α - температурний коефіцієнт опору (ТКО), який визначається експериментально.

За величиною ТКО:

 

, (3)

 

тобто фізичний зміст ТКО полягає у відносній зміну кожної початкової одиниці опору при зміні температури на один градус. Вимірюється ТКО в град^-1.

За низьких температур для багатьох металів залежність R = f(T) має інший характер (рис. 6). Тобто при певній для даного металу низькій температурі Т_к, яка називається критичною, опір падає практично до нуля. Це явище називається надпровідністю, в межах класичної теорії воно не пояснюється.

Причиною розходжень результатів класичної теорії з експериментальними фактами є те, що в цій теорії не враховуються квантові властивості електронів. З врахуванням цих властивостей виходить, що у виразі (1) величина є аналогічна середній довжині вільного пробігу електронів у металі і залежить обернено пропорційно від Т.

Величина являє собою швидкість електронів у валентній зоні і практично не залежить від Т. Таким чином, провідність металів обернено пропорційна, а опір прямопропорційний температурі Т.

Явище надпровідності пояснюється обмінною взаємодією між електронами і має квантову природу.

 

Рис. 6.

 

3. Метод вимірювань.

Метод вимірювань полягає у визначенні опору метала при різних температурах. Якщо побудувати графік залежності R = f(t°), то шляхом екстраполяції можна знайти опір метала R₀ при 0° С. Тангенс кута нахилу прямої R = f(t,°С) визначається виразом

 

(4)

 

і співпадає з величиною 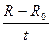в формулі (2). Отже, ТКО визначається виразом:

 

(5)

 

4. Послідовність виконання роботи.

1. Скласти електричне коло за схемою (рис. 7).

 

 

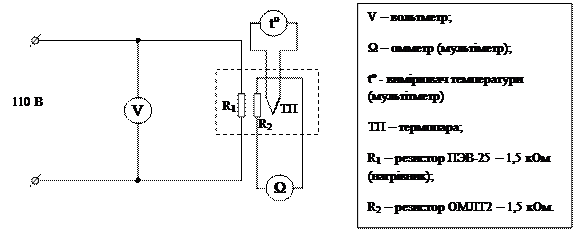Рис. 7.

2. Виміряти омметром опір метала при кімнатній температурі.

3. Увімкнути нагрівач, через кожні 10° С вимірювати мультиметром або термометром температуру металу та омметром опір металевого провідника.

 

4. Результати вимірювань занести до таблиці 1.

 

Таблиця 1.

t, °С
R, Ом

 

5. Побудувати графік залежності R=f(t,°С).

6. За графіком визначити R₀ і tgφ.

7. За формулою (5) обчислити ТКО α.

8. У висновках до роботи зазначити, який характер залежності R=f(t°С) для досліджуваного металу, і порівняти одержаний дослідним шляхом ТКО з його табличним значенням.

5. Контрольні запитання.

1. Яка будова кристалічної ґратки металів і який характер сил взаємодії в них?

2. Чому металічні кристали мають добру електропровідність?

З. Як пояснюється залежність опору металів від температури в класичній теорії електропровідності?

4. Чому при виникненні кристалів відбувається розщеплення енергетичних рівнів атомів?

5. Що називається зоною дозволених і зоною заборонених енергій?

6. Як пояснюється провідність металів на основі зонної теорії?

7. Як заповнена у металів валентна зона і де у них знаходиться зона провідності?

8. Який вигляд має експериментальна залежність опору металів від температури?

9. Що характеризує і в яких одиницях вимірюється температурний коефіцієнт опору?

10. Як пояснюється температурна залежність опору металів в квантовій теорії провідності?

11. Який метод вивчення температурної залежності металів використовується в даній роботі?

 

6. Домашнє завдання.

Для виконання роботи необхідно вивчити наступні питання курсу фізики: типи міжатомних зв'язків у твердих тілах; виникнення кристалічної ґратки; розподіл енергетичних рівнів електронів і виникнення енергетичних зон; валентна зона і зона провідності у металів; класична теорія електропровідності металів, залежність електроопору металів від температури.

7.Прилади та обладнання.

1 Досліджуваний металевий провідник.

2 Термометр.

3 Нагрівач.

4 Автотрансформатор.

5 Омметр.

 

8. Література

1. Савельев Й. В. Курс общей физики, Т. І, 1970, «Наука», §13.

2. Савельев И.В. Курс общей физики, Т. II, 1969, «Наука», §69-71.

3. Зисман Г. А., Тодес О. М. Курс общей физики, Т.І, 1970, «Наука», §19.

4. Зисман Г. А., Тодес О. М. Курс общей физики, Т.ІІ, 1969, «Наука», § 19-20.

 

Лабораторна робота №14

 

Температурна залежність електричного опору напівпровідників

 

Мета роботи.

Знайти залежність електричного опору напівпровідників від температури, визначити енергію активації і температурний коефіцієнт опору.

 

2. Теоретичні відомості.

Електричні властивості кристалічних твердих тіл визначаються будовою їхньої кристалічної ґратки і характером сил, що діють між частинками твердого тіла, тобто типом хімічного зв'язку. За квантовою теорією енергія електронів в атомах квантується, тобто може мати лише дискретні значення. Ці значення енергії відповідають енергетичним рівням. Якщо однакові атоми ізольовані один від одного, то вони мають однакові енергетичні рівні. При утворенні кристала відбувається зміна енергетичних рівнів у зв'язку з взаємодією атомів. Якщо кристал складається з N атомів, то замість одного, однакового для всіх атомів рівня, виникає N дуже близьких енергетичних рівнів, які не співпадають один з одним і сукупність яких називається зоною енергетичних рівнів. Розщеплення енергетичних рівнів відбувається згідно з принципом Паулі, за яким на одному енергетичному рівні може перебувати не більше двох електронів, які відрізняються орієнтацією спінів. Сукупність значень енергії, якими можуть мати електрони в даному атомі (зони дозволених енергій) чергуються зі значеннями енергій, які електрони в даному атомі мати не можуть (зони заборонених енергій). Ступінь розщеплення для різних рівнів неоднакова. Рівні, заповнені ближчими до ядра (внутрішніми) електронами, розщеплюються незначно, бо ці електрони слабо взаємодіють з електронами і ядрами інших атомів, які утворюють кристал. Така взаємодія є значною для валентних електронів, внаслідок чого їхні рівні розщеплюються сильніше, створюючи валентну зону. Ще помітнішим є розщеплення більш високих, ніж валентні, енергетичних рівнів, не зайнятих електронами в основному стані атома. У кристалів різних типів ступінь заповнення валентної зони різна і енергетичні зони розміщені по-різному, чим пояснюється їхня різна електропровідність. Кристали, у яких валентна зона заповнена повністю, а наступна за нею зона дозволених енергій відокремлена зоною заборонених енергій, при абсолютному нулі температури і відсутності зовнішнього збудження (підігрів, опромінення) провідності не мають. В таких кристалах електричне поле не може викликати напрямленого переміщення електронів, оскільки при напруженостях поля, які не викликають пробою кристалів, воно не може надати електронам необхідної для цього енергії. Цю додаткову енергію електрони можуть одержати при нагріванні, опроміненні та інших збудженнях кристала. Якщо внаслідок цього енергія електрона виявиться достатньою для переходу його до вільної зони дозволених енергій, яка називається зоною провідності, то в кристалі є можливим виникнення електричного струму, а такі речовини називаються напівпровідниками. Якщо заборонена зона настільки широка, що перехід електронів є неможливим, то речовина є ізолятором (діелектриком). Умовно вважають, що напівпровідниками є речовини з шириною забороненої зони менше 3 еВ, а діелектриками – кристали з шириною забороненої зони більше 3 еВ (рис. 1). Енергія ΔW, необхідна для переведення електрона в зону провідності, називається енергією ширини забороненої зони або енергією активації електронів. Чисельно енергія активації співпадає з шириною забороненої зони.

 

Зонна діаграма діелектрика та напівпровідника

 

Рис. 1.

 

При переході електронів з валентної зони в зону провідності виникають дірки – некомпенсовані позитивні заряди. На залишені електронами місця переходять електрони з більш низьких рівнів, де замість електронів виникають дірки. Таким чином, по кристалу в електричному полі переміщуються і електрони, і дірки, але в протилежних напрямках. Одночасно з виникненням вільних електронів і дірок в напівпровіднику йде зворотній процес – рекомбінація, яка призводить до попарного зникнення електронів і дірок Кожному значенню температури кристала відповідає певна рівноважна концентрація електронів і дірок, величина якої змінюється з температурою Т за законом:

 

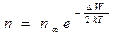, (2.1)

 

де n і n_∞ - концентрація вільних носіїв при температурах Т і Т=∞; ΔW - енергія активації електронів; k - стала Больцмана.

Температурна залежність електропровідності будь-якого матеріалу визначається залежністю концентрації носіїв струму та їхньої рухливості від температури. В напівпровідниках рухливості у електронів і дірок слабо залежать від температури, тому електропровідність залежить від температури за тим же законом що і концентрація:

 

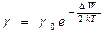, (2)

 

де γ і γ₀ - питомі електропровідності при температурах Т і Т=0. Графік залежності має вигляд (рис. 2).

 

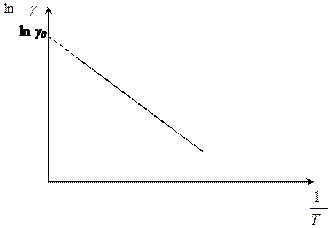Рис. 2.

 

Оскільки опір є оберненим до електропровідності, то

 

, (3)

 

де R і R_∞ опори напівпровідника при температурах Т і Т=∞. Отже, опір напівпровідників зменшується при підвищенні температури за експоненціальним законом (рис. 3).

 

Рис. 3.

Зміна опору при зміні температури характеризується температурним коефіцієнтом опору α (ТКО), який в загальному вигляді задається виразом:

 

(2.4)

 

Фізичний зміст ТКО полягає у відносній зміні кожної початкової одиниці опору при зміні температури на один градус. Вимірюється ТКО в град^-1.

Співвідношення (3) і (4) показують, що для напівпровідників

 

 

тобто α < 0, що відповідає зменшенню R при збільшенні Т і має різне значення при різних температурах. Провідність, зумовлена електронами, називається електронною (n - тип), а дірками - діркового (р - тип). В напівпровідниках, у яких відсутні домішки і дефекти кристалічної ґратки, провідність є електронно-дірковою. Вона називається власною і досягає значних величин при достатньо високих температурах. При введенні до кристала домішок або порушенні періодичності його кристалічної гратки енергетична зонна діаграма змінюється. Якщо валентність атомів домішки на одиницю більша від валентності основних атомів кристалу, то один валентний електрон домішкового атома не буде брати участі у створенні ковалентних зв'язків і, відокремившись від атома за рахунок теплового руху, стає електроном провідності. Дірка, яка виникає на місці вивільненого електрона, є зв'язаною з домішковим атомом і не зможе вільно переміщуватись в кристалі. Домішки, які дають напівпровіднику вільні електрони провідності, називаються донорами. Енергетичні рівні таких електронів називаються локальними, бо вони виникають не по всьому кристалу, а тільки там, де є домішкові атоми. Локальні рівні в напівпровідниках з донорними домішками розташовані в зоні заборонених енергій поблизу нижнього рівня зони провідності (рис. 4). З цих рівнів електрони легко переходять в зону провідності, оскільки енергія активації донорної домішки ΔW_D значно менша енергії активації ΔW власної провідності. Завдяки цьому концентрація домішкових носіїв струму при незначних температурах значно перевищує концентрацію власних носіїв, внаслідок чого в напівпровідниках з донорними домішками переважає електронна провідність.

Якщо валентність атомів домішки на одиницю менша від валентності основних атомів кристалу, то валентних електронів атома домішки буде недостатньо для створення ковалентних зв'язків. Один із зв'язків залишиться недокомплектованим і може захопити електрон.

 

Зонна діаграма напівпровідника з донорними домішками

 

 

 

Рис. 4.

 

При переході електрона на це місце в однієї з сусідніх пар виникає дірка, яка буде вільно перемішуватись по кристалу, а негативний надлишковий заряд, що з'явився поблизу домішкового атома, буде з ним зв'язаний. Домішки, за рахунок яких в напівпровіднику виникають вільні дірки, називаються акцепторними. Перехід електрона із заповненого зв'язку в валентний зв'язок відповідає переходу валентного електрона на локальний енергетичний рівень, який в такому випадку розташований в зоні заборонених енергій поблизу верхнього рівня валентної зони (рис. 5).

 

Зонна схема напівпровідника з акцепторними домішками

 

Рис. 5.

 

Оскільки енергія активації діркової (акцепторної) провідності ΔW_A мала в порівнянні з енергією активації власної провідності ΔW, то при невисоких температурах концентрація домішкових носіїв струму значно перевищує концентрацію власних носіїв, внаслідок чого в напівпровідниках з акцепторними домішками переважає діркова провідність. Наприклад, якщо в деяких вузлах ґратки германію (Gе) його 4-валентні атоми будуть заміщені 5-валентними атомами стибію (Sb), то домішка буде донорною (рис. 6). А якщо у вузлах ґратки кремнію (Si) його 4-валентні атоми будуть заміщені 3-валентними атомами бору (В), то домішка буде акцепторною (рис. 7).

При підвищенні температури концентрація домішкових носіїв швидко зростає і досягає насичення. Це відповідає повному звільненню від електронів донорних локальних рівнів або повному заповненню електронами акцепторних локальних рівнів. Проте при підвищенні температури зростає і власна провідність, зумовлена переходом електронів безпосередньо з валентної зони в зону провідності.

 

Електронний перехід у випадку донорної домішки

 

 

Рис. 6.

 

Електронний перехід у випадку акцепторної домішки

 

 

Рис. 7.

 

Таким чином, при високих температурах з’являється власна провідність.

 

3. Контрольні запитання.

1. Чому при виникненні кристалів відбувається розщеплення енергетичних рівнів атомів?

2. Що називається зоною дозволених і зоною заборонених енергій?

3. Як заповнена валентна зона у напівпровідників і де у них знаходиться зона провідності?

4. Чим відрізняється зонна структура діелектриків і напівпровідників?

5. Які носії заряду є в напівпровідниках?

6. Що називається енергією активації електронів у напівпровіднику?

7. За яким законом змінюється питома електропровідність напівпровідників при зміні температури?

8. За яким законом змінюється опір напівпровідників при зміні температури?

9. Що характеризує і в яких одиницях вимірюється температурний коефіцієнт опору?

10. Який фізичний зміст має від'ємний знак температурного коефіцієнта опору напівпровідників?

11. Що називається власною провідністю напівпровідників і при яких температурах вона є значною?

12. Що називається домішковою провідністю напівпровідників і як вона залежить від температури?

13. В чому полягає метод вимірювання температурної залежності напівпровідників в даній лабораторній роботі?

14. Який графік використовується для визначення енергії активації температурного коефіцієнта опору напівпровідника?

 

4. Домашнє завдання.

Для виконання роботи необхідно вивчити наступні питання курсу фізики: виникнення кристалічної ґратки; розщеплення енергетичних рівнів електронів і виникнення енергетичних зон; валентна зона і зона провідності в ізоляторах і напівпровідниках; власна і домішкова провідності напівпровідників; температурна залежність опору напівпровідників.

 

Лабораторне завдання.

Метод вимірювань грунтується на визначенні опору напівпровідника при різних температурах.

Якщо прологарифмувати вираз (3) і розв'язати систему рівнянь

 

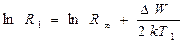
(5)

 

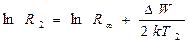
то вийде, що енергія активації провідності

 

(6)

 

Величина 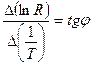є тангенсом кута нахилу залежності R=f(T) побудованої в координатах (рис. 8). Таким чином, для енергії активації одержимо вираз

 

(7)

 

для термічного коефіцієнта опору одержимо вираз

 

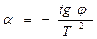, (8)

 

де

 

Залежність опору напівпровідника від температури

 

Рис. 8.

6. Послідовність виконання роботи

1. Скласти електричне коло за схемою (рис. 9).

 

Схема вимірювальної установки

		V – вольтметр; Ω – омметр (мультиметр); tº - вимірювач температури (мультиметр) ТП – термопара; R1 – резистор ПЭВ-25 – 1,5 кОм (нагрівник); R2 – напівпровідник.

 

Рис. 9.

 

2. Виміряти омметром або мультиметром опір напівпровідника при кімнатній температурі.

3. Увімкнути нагрівач. Через кожні 5 - 10° вимірювати термометром або мультиметром температуру напівпровідника і омметром або мультиметром його опір.

4. Результати вимірювань і обчислень занести до Таблиці 1.