Визначення значень та методом сум

Середини часткових інтервалів Тсі,	Частоти mi	Допоміжні коефіцієнти
К1= 25	К2= 7
			-
		-	-
			-
	N = 40	Л1= 5	Л2 = 1

 

В дві перші графи табл. 3.4 переписують значення з 1-го та 2-го рядків табл. 3.1. В третій графі табл. 3.4 роблять прочерк проти найбільшого значення частоти m_i (в нашому прикладі це 17), а в четвертій графі – три прочерку: проти прочерку в тертій графі та зверху і знизу від нього. Далі в третій графі виконують послідовно додавання наростаючим підсумком значень m_i по часткових інтервалах, починаючи від першого значення до прочерку та від останнього значення до прочерку.

Одержані суми складають і підраховують значення двох допоміжних коефіцієнтів К₁ та Л₁. Аналогічно одержують значення допоміжних коефіцієнтів К₂ та Л₂ по четвертій графі. Потім підраховуються допоміжні коефіцієнти М₁ = К₁- Л₁ і М₂ = К₁+ Л₁ + 2К₂+ 2Л₂ потім визначають середнє арифметичне значення напрацювання клинових пасів до першого відказу та вибіркове середнє квадратичне відхилення по рівняннях:

; (3.2)

(3.3)

де Т_{с max} – значення середини часткового інтервалу з максимальною частотою відказів, напроти якого зроблений прочерк в третій графі;

значення напрацювання в границях часткового інтервалу (в нашому прикладі 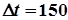г).

Результати розрахунків:

г,

Ступінь розсіювання випадкової величини визначається безрозмірною числовою характеристикою – коефіцієнтом варіації:

 

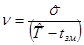, (3.4)

 

де t_зм - величина зміщення зони розсіювання Т₁ відносно нульового значення

Зміщення необхідно приймати чисельно рівним нижній границі першого часткового інтервалу. З таблиць рядів розподілу випадкових величин в наших прикладах у випадку клинових пасів t_зм=0, а у випадку колінчастих валів t_зм=0,5 тис. мото-г. так у випадку клинових пасів коефіцієнт варіації підраховується по рівнянню:

 

Даний безрозмірний коефіцієнт не тільки використовується як відносна характеристика ступеню розсіювання випадкової величини відносно середнього значення, але і для орієнтованого вибору теоретичного закону розподілу (ТЗР) випадкової величини. Стосовно до завдання, що розглядається, при

n £ 0,33 – закон розподілу вибирається нормальний, а при n > 0,33 – закон розподілу Вейбулла.

Оскільки в першому прикладі значення n < 0,33, приймаємо для подальших розрахунків нормальний закон розподілу напрацювання клинових пасів до першого відказу. Цей орієнтований висновок необхідно в подальшому перевірити за допомогою критерію О.М.Колмогорова [1, 2, 3, 4].

 

3.4. Статистична оцінка ймовірності безвідказного напрацювання та інтенсивності відказів 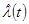клинових пасів для і-х часткових інтервалів підраховують в наступних рівняннях:

, (3.5)

де N – число виробів с початку випробувань (в розглянутому завданні

N = 40);

- значення напрацювання в частковому інтервалі (у кожному прикладі 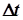= 150 г.)

N(t_і) – кількість робото здатних виробів до початку і-го часткового інтервалу

Вихідні дані для підрахунків та їх результати зводять в табл. 3.5

Таблиця 3.5.

Визначення статистичних оцінок 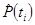та

Показники	Значення показників по часткових інтервалах
0...150	150...300	300...450	450...600	600...750	750...900
1.Кількість відказів за інтервал, mi
2.Кількість виробів, що відмовили до кінця інтервалу, Smi
3. Кількість роботоздатних виробів до початку інтервалу, N(ti)
4.Статистична оцінка,	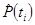0,975	0,875	0,525	0,100	0,025
5. Статистична оцінка,	0,0002	0,0007	0,0027	0,0054	0,0050	0,0067

 

3.5. Графік зміни дослідної ймовірності безвідказної роботи будують з використанням відповідних їх значень для часткових інтервалів з табл. 3.5.

Приклад побудови графіка показаний на рис. 3.4.

Між показниками ймовірності безвідказної роботи виробу та інтегральною функцією розподілу напрацювання до першого відказу існує взаємозв’язок, обумовлений рівнянням

 

_і (3.6)

 

 

Рис. 3.4. Емпірична та теоретична інтегральна функції розподілу напрацювання клинових пасів до першого відказу та ймовірність безвідказної роботи пасів по даних випробувань на надійність.

 

Лабораторна робота №2