Виконання прикладу завдання по першій лабораторній роботі

3.1. По умові завдання необхідно визначити числові значення показників надійності приводних клинових пасів (колінчастих валів) по результатах випробувань 40^а однотипних зразків.

Так клинові паси являються виробами, що не ремонтуються, тому основними показниками їх надійності є диференційна f(t) та інтегральна F(t) функції розподілу напрацювання цих виробів до першого відказу, ймовірність безвідказної роботи Р(t), середнє напрацювання до першого відказу , інтенсивність відказів l(t).

Ці ж показники безвідказності визначаються і для виробу, що ремонтується (колінчастого валу) по результатах спостережень напрацювань до першого відказу (додатки 2 та 3).

Числові значення показників надійності визначають по результатах спостережень за випробуваннями однотипних виробів в заданих умовах, фіксуючи напрацювання окремих виробів до першого відказу в годинах (мото-год, для колінчастих валів) роботи під навантаженням. Результати спостережень подають у вигляді інтервального статистичного ряду розподілу напрацювання виробів до першого відказу, які і розміщені в додатках 1 та 2

Для вказаного вище зразкового завдання часткові інтервали значень напрацювання Т_і приймаються по варіанту 11 (додаток 1), а значення частот m_i відказів пасів по і-х частових інтервалах (додаток 3). У випадку колінчастих валів для інтервального ряду (додаток 2 – варіант 1), а для значень частот (додаток 3 – варіант 6).

Інтервальний статистичний ряд емпіричного розподілу напрацювання Т₁ для заданих умов наведений в табл. 3.1. В цій же таблиці вказані значення частостей (емпіричних імовірностей) 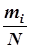та накопичених частостей 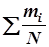по окремих інтервалах. Сума частот Sm_i по всіх інтервалах повинна бути рівна N, тобто 40, а сума накопичених частостей 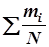= 1.

Таблиця 3.1.

Інтервальний статистичний ряд емпіричного розподілу клинових пасів до першого відказу

Параметри	Значення часткових інтервалів, г
0...150	150...300	300...450	450...600	600...750	750..900
1.Середини інтервалів Тсі, г.
2.Частоти mi
3. Частості mi/N	0,025	0,100	0,350	0,425	0,075	0,025
4. Накопиченні частості Smi/N[Fe(t)]	0,025	0,125	0,475	0,900	0,975	1,00

 

3.2. Дані табл. 3.1. використовуються для побудови графіків, які наочно характеризують емпіричні розподіли випадкових величин – гістограми, полігона та інтегральної функції емпіричного розподілу напрацювання.

Для побудови гістограми по горизонтальній осі графіка відкладають значення, які відповідають границям часткових інтервалів, а на вертикальній – частоти та частості по окремих інтервалах. Далі будуються прямокутники, основи яких лежать на горизонтальній осі координат і дорівнюють значенням часткових інтервалів, а висоти дорівнюють частотам або частостям відповідних інтервалів (табл. 3.1.). В результаті одержуємо ступінчастий багатокутник або гістограму.

Якщо з’єднати прямими лініями середини верхніх горизонтальних сторін прямокутників гістограми, то одержимо полігон розподілу у вигляді ламаної лінії.

Приклад побудови гістограми та полігона розподілу напрацювання клинових пасів до першого відказу наведений на рис. 3.1. На рис. 3.2 показані диференційні функції (гістограма та полігон частостей розподілу напрацювання колінчастих валів двигуна “Д-65Н” до першого відказу (додаток – 2 – варіант 1; додаток 3 – варіант 6) у випадку зміщення інтервального ряду.

 

 

Найбільш загальною характеристикою розподілу як дискретних так і неперервних випадкових величин є інтегральна функція розподілу F(T), яка визначає ймовірність тої події, що випадкова величина Т буде менша або рівна наперед заданому значенню t, тобто F(T) = Р(Т£ t). Емпірична інтегральна функція розподілу визначає частість (дослідну ймовірність) події Т£ t, а теоретична інтегральна функція розподілу – ймовірність даної події.

Функція розподілу F(T) може бути задана аналітично або представлена у вигляді графіка (рис. 3.3).

На рис. 3.3 наведений приклад побудови емпіричних інтегральних функцій напрацювання клинових пасів до відказу та напрацювання колінчастих валів до першого відказу (див. рис. 3.2, для колінчастих валів – вихідні дані: додаток 2 – варіант 1, додаток 3 – варіант 6).

У випадку дослідження напрацювання колінчастих валів до першого відказу (рис. 3.3, крива 2).

для Т_і£ 0,5 тис. мото-г.

Таким чином, початкова точка ломаної лінії лежить на осі абсцис і відповідає значенню Т₁ = 0,5 тис. мото-г.

Частість для значень Т₁£ 1,5 тис. мото-г.; в результаті визначається друга точка ломаної лінії. яку відрізками прямої з’єднують з початковою та третьою точкою, яка відповідає верхній границі інтервалу (S + для Т₁£ 2,5 тис. мото-г.). Так, переходячи послідовно від одного інтервалу до другого, поступово будують графік емпіричної функції розподілу Т₁, остання точка якої відповідає

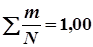для Т_і£ 6, 5 тис. мото-г.

 

 

Рис. 3.3 Експериментальні функції розподілу напрацювання клинових пасів та колінчастих валів до першого відказу.

 

3.3. Числові значення статистичних характеристик розподілу випадкової величини, таких, як середнє арифметичне значення , вибіркове середнє квадратичне відхилення підраховують по слідуючи формулах:

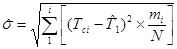, ,,(3.1)

де Т_сі – значення середини і-го інтервалу;

і – кількість інтервалів інтервального ряду;

- значення частостей (досліджених ймовірностей) по кожному і-му інтервалу.

Програми розрахунку та на мові Бейсик наведені в табл. 3.2 та 3.3.

Таблиця 3.2

Програма розрахунку середнього значення

10 REM

15 DIN T(50), M(50)

20 S = 0

30 PRINT ROL INTERVALOW – N1”

40 INPUT NL

50 PRINT “OBEM VIBORKI NO”

60 INPUT NO

70 FOR J=1 TO N1

80 PRINT “SREDN I KOL “J” – GO INTERVALA”

90 INPUT T(J), N(J)

100 S=S+T(J) M(J)

110 NEXT J

120 TO=S/NO

130 PRINT TO

 

 

Таблиця 3.3

Програма розрахунку вибіркового значення середнього

квадратичного відхилення

10 REM-OHREDEL SKW

20 DIN T(50), M(50)

25 S = 0

30 PRINT ROL INTERVALOW – N1”

40 INPUT NL

50 PRINT “OBEM VIBORKI NO”

60 INPUT NO

70 PRINT-“SREDNEE –TO”

80 INPUT TO

90 FOR J=1 TO N1

100 PRINT “SREDN I KOL “J” – GO INTERVALA

110 INPUT T(J), N(J)

120 S=S+(T(J)-TO) 2 M(J)

130 NEXT J

140 A=SQR (S/NO)

150 PRINT A

160 END

 

Для розрахунку значень 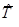та можна також використати простий метод сум. Для прикладу, що розглядається у випадку клинових пасів наведена розрахункова таблиця для використання метода сум (табл. 3.4).

Таблиця 3.4