Условное математическое ожидание двумерного дискретного случайного вектора и функция регрессии

E[h(Y)|X=x_i]=СУМ(j=1..m)(h(y_j)P(Y=y_j | X=x_i)

Если для любого X=x_i выполняется: g(x_j)=E[Y | X=x_i], то g(x)=E[Y|X] – ф-ия регрессии Y по X/

Полиномиальное распределение и его характеристики.

n независимых повторных испытаний. Исходы: A₁, …, A_k – полная группа, если x_j – число появлений A_j в n испытаниях, то (x₁…x_k)^T имеет полином. расп:

P(X₁=m₁…X_k=m_k)=n!/(m₁!...m_k!)Произв(j=1..k)(p_j^mj)

M[ 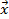]=n()

При j₁<>j₂:

M[x_j1x_j2]=n(n-1)p_j1p_j2-np_j1np_j2 = -np_j1p_j2

 

Многомерное гипергеометрическое распределение и его характеристики.

Совокупность из N элементов, среди которых D₁ – 1-го типа,…, D_k – k-го типа. Из нее извлекаются n элементов. Если x_j – число появлений элементов j-го типа, то (x₁…x_k)^T имеет многомерное гипергеометрическое распределение:

p(x₁= m₁…x_k= m_k)=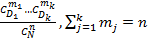

Понятие непрерывного случайного вектора.

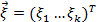имеет абсолютно непрерывное распределение если оно может быть задано с помощью ф-ии плотности распределения.

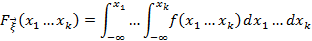
Плотность распределения.

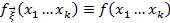– плотность 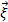, если для любых справедливо

 

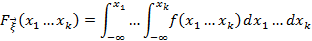
Свойства плотности абсолютно непрерывного случайного вектора.

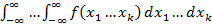1) =1

2)

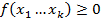
3)

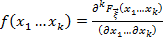
4) При m<k: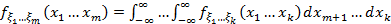

 

Условная функция распределения вектора.

F(x, y) – совместная фр (X, Y), тогда для любого B из R с вероятностной мерой >0:

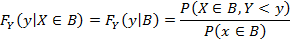
При B={x:x<=X<x+Δx} при Δx>0:

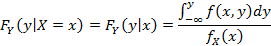
Условная плотность распределения случайного вектора.

=

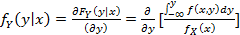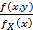
Условные характеристики компонент случайного вектора.

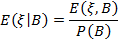
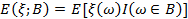
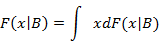
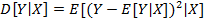
Свойства математического ожидания случайной величины.

1) M[C]=C

2) M[kX]=kM[X]

3) M[X1+X2+…Xn]= M[X1]+M[X2]+…+M[Xn]

4) M[XY]=M[X]M[Y] X, Y - независимы

Свойства дисперсии случайной величины.

1) D[C]=0

2) D[X+C]=D[X]

3) D[cX]=c²D[X]

4) D[aX+b]=a²D[X]

5) Для нз X, Y: D[X+Y]=D[X]+D[Y]

Свойства ковариационного момента случайных величин.

1) Если X, Y – нз, то K(X, Y)=0

2) |K(X,Y)|<=sqrt(D[X]D[Y])

Свойства коэффициента корреляции.

1) Если X и Y – нз, то r(X, Y)=0

2) |r(X,Y)|=1 (?)

Применения свойств числовых характеристик к анализу портфеля инвестиций, среднего, стандартизованной с.в., нахождению числовых характеристик гипергеометрического распределения.

(?)

Основные способы нахождения распределения функции от случайного вектора.

1) Универсальный подход

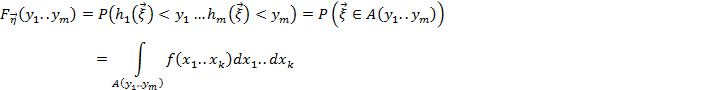
2) Замена переменной

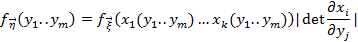
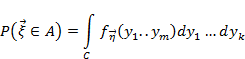
3) По св-вам УМО

Если , то

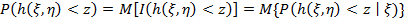
Нахождение распределения суммы, разности, частного и произведения двух случайных величин.

Z=XY,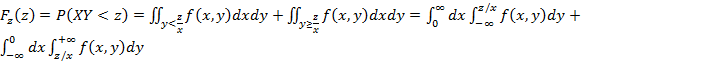

Понятия случайной функции и процесса, временного ряда.

Случайный процесс – мат. модель для описания случайных явлений, развивающихся во времени.

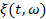- состояние процесса в текущий момент – векторная или скалярная величина.

Случайная функция – семейство с.в. , определенных на (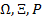) где TϵR

Если t-время, то сф = случайный процесс

Временной ряд - Последовательность наблюдений моделируемого показателя, упорядоченная в порядке возрастания времени.