Любое звено динамической системы может быть описано с помощью одного дифференциального уравнения. Однако одной и той же передаточной функции может соответствовать множество структур моделей. Отсюда вытекает необходимость выбора наиболее рациональной модели при математическом описании динамических систем. На практике отдают предпочтение так называемым каноническим формам. С инженерной точки зрения канонические формы – это модели исходной системы, отличающиеся простотой математического описания и регулярной структурой. Это обеспечивается переходом от исходного описания с помощью замены переменных к такой системе координат, что большинство элементов матриц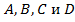 
в новой системе координат становятся равными нулю или единице.
Наиболее распространенными в практике каноническими формами являются:
Ø каноническая форма Фробениуса;
Ø каноническая форма Жордана.
Наибольший интерес представляют канонические формы, при которых структура матриц 
имеет наиболее простой вид. Причем, при приведении уравнений к канонической форме простую структуру принимают две матрицы из трех:
a) матрицы 
управляемые канонические формы;
b) матрицы 
наблюдаемые канонические формы.
Основу реализации фробениусовой канонической формы составляет цепочка последовательно включенных интеграторов, охваченных обратными связями, причем, коэффициенты обратных связей совпадают с коэффициентами характеристического полинома динамической системы.
Для формирования уравнения состояния во фробениусовой канонической форме, необходима передаточная функция исследуемой системы:
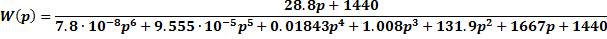
Здесь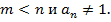 
Запишем дифференциальное уравнение исследуемой системы:
Произведем следующие замены:
Пусть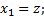 
;
.
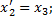
Тогда из уравнения (16) следует, что
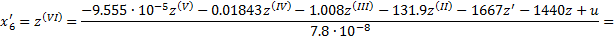
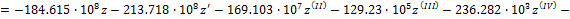
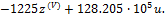
Таким образом,
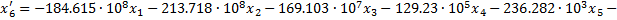
Из уравнения (17) следует, что
Объединим получившиеся дифференциальные уравнения и уравнение выхода (16) в систему
Матричная запись этих уравнений имеет следующий вид:
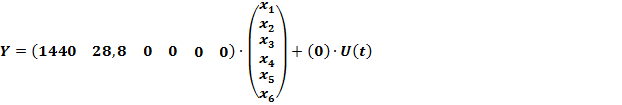(21)
Полученная форма уравнений состояния носит название фробениусовой канонической формы.
Построим граф, соответствующий данной канонической форме. Графы используются для наглядного изображения зависимостей в САУ. Граф – это условное графическое изображение системы уравнений. Граф представляет собой совокупность вершин (узлов) и соединяющих их ветвей (дуг) с обозначением направления передачи сигналов и их пропускной способности. В данном случае вершинами графа являются переменные 
входной сигнал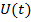 
, выходной сигнал 
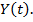Связи между переменными изображаются в виде дуг с проставленными коэффициентами при переменных и направлениями передачи сигнала.
Рис. 4. Граф системы для фробениусовой канонической формы.
