Коэффициент теплоотдачи представляет собой количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и жидкостью, равной одному градусу:
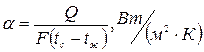
Процесс теплоотдачи является сложным процессом, а коэффициент теплоотдачи является сложной функцией различных величин, характеризующих этот процесс. В общем случае коэффициент теплоотдачи является функцией формы  , размеров
, размеров  ,
,  ,…, температуры поверхности нагрева
,…, температуры поверхности нагрева  , скорости жидкости
, скорости жидкости 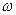 , ее температуры
, ее температуры  , физических свойств жидкости – коэффициента теплопроводности
, физических свойств жидкости – коэффициента теплопроводности  , удельной теплоемкости
, удельной теплоемкости 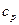 , плотности
, плотности  , коэффициента вязкости
, коэффициента вязкости 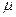 и других факторов:
и других факторов:
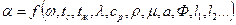
Задача 1
Показать сравнительным расчетом целесообразность применения пара высоких параметров на примере паротурбинной установки, работающей по циклу Ренкина, определив для двух значений начального давления  и начальной температуры
и начальной температуры  (при одинаковом конечном давлении
(при одинаковом конечном давлении  ), термический КПД цикла и теоретический удельный расход пара. Схему решения представить в
), термический КПД цикла и теоретический удельный расход пара. Схему решения представить в  - диаграмме. Изобразите схему ПТУ, дайте ее краткое описание. Для второго варианта определить также внутреннюю энергию пара перед конденсатором.
- диаграмме. Изобразите схему ПТУ, дайте ее краткое описание. Для второго варианта определить также внутреннюю энергию пара перед конденсатором.
Значения параметров принять по таблице 2.
На основе расчета проанализировать характер зависимости термического КПД паротурбинной установки от изменения начальных параметров пара.
Объяснить, чем ограничены выбор параметров перегретого пара и давления в конденсаторе.
Задачу решить с помощью  - диаграммы.
- диаграммы.
Таблица 2 - Исходные данные
| Последняя цифра шифра | 1 вариант | Предпоследняя цифра шифра | 2 вариант | ||
| Параметры пара | Параметры пара | ||||

| 
| 
| 
| ||
| 5,0 | 13,0 |
Решение

Рисунок 1.1 - Схема паросиловой установки (цикл Ренкина): 1 - котел; 2 - пароперегреватель; 3 - паровая турбина; 4 - электрогенератор; 5 - конденсатор; 6 - насос.

Рисунок 1.2 - цикл Ренкина в  и
и 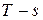 координатах.
координатах.
В паровом котле 1 вода при постоянном давлении нагревается до температуры насыщения (давления) 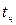 (линия 4-5 на рис.3.2), затем в результате подвода теплоты
(линия 4-5 на рис.3.2), затем в результате подвода теплоты 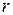 происходит изобарно - изотермический процесс парообразования (линия 5-6). В пароперегревателе 2 происходит перегрев пара (изобарный процесс 6-1) - повышение температуры пара выше
происходит изобарно - изотермический процесс парообразования (линия 5-6). В пароперегревателе 2 происходит перегрев пара (изобарный процесс 6-1) - повышение температуры пара выше 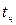 от состояния сухого насыщенного пара (точка 6) до заданной температуры перегрева (точка 1). В паровой турбине 3 пар расширяется адиабатно (линия 1-2) от давления
от состояния сухого насыщенного пара (точка 6) до заданной температуры перегрева (точка 1). В паровой турбине 3 пар расширяется адиабатно (линия 1-2) от давления  до давления
до давления  в конденсаторе.
в конденсаторе.
В конденсаторе 4 при постоянных давлении и температуре этот пар полностью конденсируется 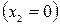 , отдавая теплоту охлаждающей воде. Конденсат насосом 5 изохорно (ввиду несжимаемости жидкости) перекачивается в паровой котел (линия 3-4). Так как в насосе практически температура конденсата не повышается (точка 4), о в
, отдавая теплоту охлаждающей воде. Конденсат насосом 5 изохорно (ввиду несжимаемости жидкости) перекачивается в паровой котел (линия 3-4). Так как в насосе практически температура конденсата не повышается (точка 4), о в 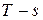 -диаграмме точки 3 и 4 оказываются совмещенными. Процесс 4-5 нагрева конденсата до температуры
-диаграмме точки 3 и 4 оказываются совмещенными. Процесс 4-5 нагрева конденсата до температуры 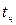 совпадает в
совпадает в 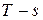 -диаграмме с нижней пограничной кривой
-диаграмме с нижней пограничной кривой 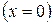 . Далее цикл Ренкина повторяется.
. Далее цикл Ренкина повторяется.
Первый вариант: 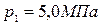 ,
,  ,
,  .
.
Значения энтальпий  и температуру воды
и температуру воды  (конденсата) находим по диаграмме
(конденсата) находим по диаграмме 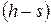 :
:  ,
,  ,
,  ,
, 
Работа получаемая в турбине:
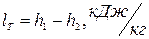 (1.1)
(1.1)

Термический  цикла:
цикла:
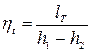 (1.2)
(1.2)
где 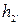 - энтальпия питательной воды,
- энтальпия питательной воды, 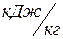 ;
;
 (1.3)
(1.3)
тут  - удельная теплота воды при постоянном давлении,
- удельная теплота воды при постоянном давлении,  ;
;

Поставляя полученное значение в формулу (1.3), находим

Теоретический удельный расход пара:
 (1.4)
(1.4)

Второй вариант:  ,
,  ,
,  .
.
Значения энтальпий  и температуру воды
и температуру воды  (конденсата) находим по диаграмме
(конденсата) находим по диаграмме 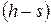 :
:  ,
,  ,
,  ,
, 
Работа получаемая в турбине:
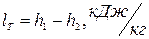 (1.5)
(1.5)

Термический  цикла:
цикла:
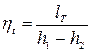 (1.6)
(1.6)

Теоретический удельный расход пара:
 (1.7)
(1.7)

Внутренняя энергия пара перед конденсатором:
 (1.8)
(1.8)
где 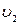 - удельный объем влажного насыщенного пара в точке 2, который находим по
- удельный объем влажного насыщенного пара в точке 2, который находим по  - диаграмме
- диаграмме 

Сравнение результатов расчета свидетельствует о том, что при переходе к парам более высоких параметров термический КПД цикла увеличивается и происходит увеличение экономичности цикла паротурбинной установки.
Исследование термического к.п.д. цикла Ренкина при различных начальных и конечных состояниях пара позволяет сделать вывод, что с увеличением начального давления и начальной температуры пара и понижением конечного давления в конденсаторе к.п.д. паротурбинной установки растет. Повышение температуры перегрева пара ограничивается способностью металла, из которого сделаны трубы, выдерживать большие давления при высоких температурах, то есть конечные параметры пара определяются наличием относительно дешевых жаропрочных металлов.
Понижение давления в конденсаторе является особенно эффективным средством для повышения термического к.п.д. паротурбинной установки, но выбор конечного давления в конденсаторе определяется температурой охлаждающей воды, так как для интенсивного теплообмена разность температур между паром и охлаждающей водой должна быть 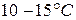 .
.

Рисунок 3 - Определение энтальпии пара в процессе цикла Ренкина по диаграмме 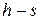
Задача 2
Сжатие воздуха в компрессоре происходит: а) по изотерме, б) по адиабате. Расход воздуха  , начальное давление
, начальное давление  , начальная температура
, начальная температура  , степень сжатия
, степень сжатия  .
.
Определить для обоих вариантов величину теоретической работы сжатия, мощности компрессора, а также изменения внутренней энергии и энтропии при сжатии.
Теплоемкость воздуха  считать
считать  . Данные для решения задачи принять по таблице 3.
. Данные для решения задачи принять по таблице 3.
Таблица 3 – Исходные данные
| Последняя цифра шифра | 
| 
| Предпоследняя цифра шифра | 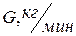
|
| 6,5 |
Решение
Параметры в начале процесса сжатия:  ;
; 
Расход всасываемого воздуха находим по уравнению состояния идеального газа:
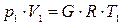 (2.1)
(2.1)
где  - газовая постоянная воздуха,
- газовая постоянная воздуха,  ;
;
Выражаем уравнение (2.1) относительно объема:
 (2.2)
(2.2)

Изотермическое сжатие
Степень сжатия:
 (2.3)
(2.3)
Теоретическая работа сжатия (абсолютное значение):
 (2.4)
(2.4)

Мощность компрессора:
 (2.5)
(2.5)

Изменение внутренней энергии при сжатии:

Изменение энтропии при сжатии:
 (2.6)
(2.6)

Адиабатное сжатие
Температуру сжатого воздуха на выходе из компрессора находим из соотношения параметров в адиабатном процессе:
 (2.7)
(2.7)
где 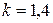 - показатель адиабаты воздуха;
- показатель адиабаты воздуха;
из формулы (2.7) находим
 (2.8)
(2.8)

Теоретическая работа компрессора (абсолютное значение):
 (2.9)
(2.9)

Мощность компрессора:
 (2.10)
(2.10)

Изменение внутренней энергии при сжатии:
 (2.11)
(2.11)
где  -массовая теплоемкость при постоянном объеме,
-массовая теплоемкость при постоянном объеме,  ;
;
 (2.12)
(2.12)
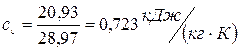
Подставляя полученное значение в формулу (2.11), находим
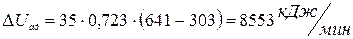
Изменение энтропии при сжатии:
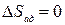
Задача 3
Водяной пар, имеющий начальное давление  и температуру
и температуру  или степень сухости
или степень сухости  (табл.4) дросселируется в трубопроводе до давления
(табл.4) дросселируется в трубопроводе до давления  (табл.5). Построить в диаграмме
(табл.5). Построить в диаграмме  условный процесс дросселирования водяного пара. Схему построения процесса дросселирования привести в тетради. Определить температуру, энтальпию, энтропию и внутреннюю энергию пара в конце процесса дросселирования.
условный процесс дросселирования водяного пара. Схему построения процесса дросселирования привести в тетради. Определить температуру, энтальпию, энтропию и внутреннюю энергию пара в конце процесса дросселирования.
Таблица 4
| Последняя цифра шифра | Начальные параметры пара | ||

| 
| 
| |
| 1,5 | - |
Таблица 5
| Последняя цифра шифра | Конечное давление 
|
| 0,16 |
Решение
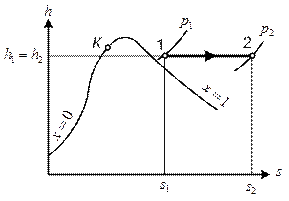
Рисунок 3.1 – Процесс дросселирования водяного пара в  координатах
координатах
На  - диаграмме водяного пара на пересечении изобары
- диаграмме водяного пара на пересечении изобары 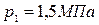 и изотермы
и изотермы  находим точку 1, характеризующую состояние пара в начале процесса дросселирования. Точка 1 находится в области перегретого пар. Энтальпия пара в точке 1 составляет
находим точку 1, характеризующую состояние пара в начале процесса дросселирования. Точка 1 находится в области перегретого пар. Энтальпия пара в точке 1 составляет  .
.
Процесс дросселирования протекает при постоянной энтальпии, поэтому точку 2, характеризующую состояние пара в конце процесса дросселирования, находим на пересечении изоэнтальпы 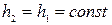 и изобары
и изобары  . Точка 2 находится в области перегретого пара. Параметры пара в точки 2:
. Точка 2 находится в области перегретого пара. Параметры пара в точки 2: 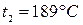 ,
,  ,
,  .
.
Внутренняя энергия пара в конце процесса дросселирования:
 (3.1)
(3.1)
где 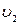 - удельный объем влажного насыщенного пара в точке 2, который находим по
- удельный объем влажного насыщенного пара в точке 2, который находим по  - диаграмме
- диаграмме 

Задача 4
Вычислить допустимую силу тока для провода диаметром  , покрытого изоляцией толщиной
, покрытого изоляцией толщиной 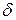 , при условии, что максимальная температура изоляции не должна быть выше
, при условии, что максимальная температура изоляции не должна быть выше 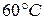 , а на внешней поверхности изоляции
, а на внешней поверхности изоляции  . Коэффициент теплопроводности материала изоляции
. Коэффициент теплопроводности материала изоляции  . Электрическое сопротивление провода
. Электрическое сопротивление провода  .
.
Данные принять по таблице 6.
Таблица 6
| Последняя цифра шифра | 
| 
| Предпоследняя цифра шифра | 
| 
|
| 2,8 | 1,3 | 0,25 | 0,0025 |
Решение
Линейная плотность теплового потока для цилиндрической стенки:
 (4.1)
(4.1)
где  - температуры внутренней и наружной поверхности изоляции,
- температуры внутренней и наружной поверхности изоляции,  ;
;
 - внутренний и наружный диаметр изоляции,
- внутренний и наружный диаметр изоляции,  ;
;
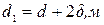 (4.2)
(4.2)

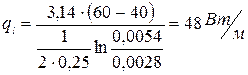
Допустимую силу тока определяем из уравнения баланса энергии:
 (4.3)
(4.3)
откуда
 (4.4)
(4.4)

Задача 5
Вычислить температуры на поверхностях стенки и тепловой поток через 1  чистой поверхности парогенератора, если заданы следующие величины: температура газов
чистой поверхности парогенератора, если заданы следующие величины: температура газов  , температура кипящей воды
, температура кипящей воды 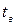 , коэффициенты теплоотдачи от газов к стенке
, коэффициенты теплоотдачи от газов к стенке  , от стенки к кипящей воде
, от стенки к кипящей воде 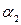 , коэффициент теплопроводности материала стенки
, коэффициент теплопроводности материала стенки  и толщина стенки
и толщина стенки 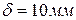 .
.
Решить задачу при условии, что в процессе эксплуатации поверхность нагрева парового котла со стороны дымовых газов покрылась слоем сажи толщиной  и со стороны воды слоем накипи толщиной
и со стороны воды слоем накипи толщиной  (соответственно, коэффициенты теплопроводности сажи
(соответственно, коэффициенты теплопроводности сажи  и накипи
и накипи  . Сравнить результаты расчетов для обоих случаев и определить уменьшение тепловой нагрузки в процентах. Построить график распределения температур.
. Сравнить результаты расчетов для обоих случаев и определить уменьшение тепловой нагрузки в процентах. Построить график распределения температур.
Данные для решения принять по табл.7.
Таблица 7
| Последняя цифра шифра | 
| 
| 
| 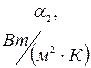
| Предпоследняя цифра шифра | 
| 
|
| 2,4 | 1,5 |
Решение
Тепловой поток через 1  чистой поверхности парогенератора:
чистой поверхности парогенератора:
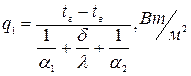 (5.1)
(5.1)

Тепловой поток через 1  загрязненной поверхности парогенератора:
загрязненной поверхности парогенератора:
 (5.2)
(5.2)

Значения температур на поверхности стенки:
 (5.3)
(5.3)

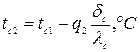 (5.4)
(5.4)

 (5.5)
(5.5)

 (5.6)
(5.6)
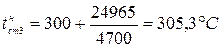
При покрытии поверхности нагрева парового котла со стороны дымовых газов покрылась слоем сажи, а со стороны воды слоем накипи тепловая нагрузка уменьшается на  .
.

Рисунок 5.1 – График распределения температур
Список использованной литературы
1 Белинский С.Я., Липов Ю.М. Энергетические установки электростанций. М., Энергия. 1984.
2 Немцов З.Ф., Арсентьев Г.В. Теплоэнергетические установки и теплоснабжение. М., Энергоиздат, 1986.
3 Нащокин В.В. Техническая термодинамика и теплопередача. М., Высшая школа, 1982.
4 Щукин А.М., Сушкин И.Н., Бахмачевский Б.И., Лызо Г.П. Теплотехника. М.,1983.
5 Михеева И.М. Основы теплопередачи. М., Энергия.1982.
6 Кириллин В.А., Сычев В.В., Шейндлин Е.А. Техническая термодинамика. М.,1985.
7 Исаченко В.Н., Осипова В.М., Сукомел А.С. Теплопередача. М.,1981.






