Теорема о сумме конечного числа бесконечно малых функций различных порядков малости

Теорема (об ограниченности сходящейся последовательности).

Всякая сходящаяся последовательность ограничена.

Доказательство:

Пусть сходится, и пусть . Тогда для положительного числа существует номер такой, что при выполняется неравенство 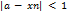. Отсюда 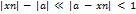, т.е. .

Следовательно, , и последовательность ограничена.

Теорема доказана.

2.

Если функция 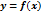представима при в виде суммы постоянного числа и бесконечно малой величины то .

Обратно, если , то , где – бесконечно малая при .

Доказательство:

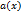Докажем первую часть утверждения. Из равенства следует . Но так как – бесконечно малая, то при произвольном найдется – окрестность точки a, при всех x из которой, значения 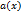удовлетворяют соотношению Тогда . А это и значит, что .

Если , то при любом для всех из некоторой – окрестность точки 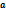будет . Но если обозначим , то 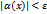, а это значит, что – бесконечно малая.

3.

Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Доказательство:

Приведем доказательство для двух слагаемых. Пусть где . Нам нужно доказать, что при произвольном сколь угодно малом найдется , такое, что для x, удовлетворяющих неравенству , выполняется .

Итак, зафиксируем произвольное число ε > 0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ₁ > 0, что при |x – a|< δ₁ имеем |α(x)|< ε / 2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ₂ > 0, что при |x – a|< δ₂ имеем | β(x)|< ε / 2.

Возьмем δ=min{ δ₁, δ₂ }. Тогда в окрестности точки a радиуса δ будет выполняться каждое из неравенств |α(x)|< ε / 2 и | β(x)|< ε / 2. Следовательно, в этой окрестности будет

|f(x)|=| α(x)+β(x) | ≤ |α(x)| + | β(x)| < ε /2 + ε /2= ε,

т.е. |f(x)|< ε, что и требовалось доказать.

 

4.

Произведение бесконечно малой функции на ограниченную функцию при (или при ) есть бесконечно малая функция.

Доказательство:

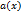Так как функция ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a . Кроме того, так как – бесконечно малая функция при x , то для произвольного ε > 0 найдется окрестность точки a, в которой будет выполняться неравенство . Тогда в меньшей из этих окрестностей имеем .

А это и значит, что – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.

5.

Теорема о связи между бесконечно большой и бесконечно малой функциями:

Если функция - функция бесконечно малая, то функция есть бесконечно большая функция и наоборот.

Доказательство:

 

Пусть - бесконечно малая функция при , т.е. . Тогда для любого числа существует такое число , что для всех x, удовлетворяющих неравенству

, выполняется неравенство , т.е. , т.е. ,

где . А из этого следует, что функция - бесконечно большая.

 

6.

 

7.

Теорема о сумме конечного числа бесконечно малых функций различных порядков малости.

Теорема: сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.

 

Доказательство:

Пусть при , причем - бесконечно малая более высокого порядка малости, чем , т.е. .

Тогда: .

 

Следовательно: при .