А.1 Формулы для оценивания погрешности эталонов
А.1.1 Воспроизводимая единица величины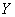 
в большинстве случаев зависит от других измеряемых входных величин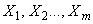 
, (A.1)
где 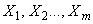- непосредственно измеряемые входные величины, влияющие на размер единицы эталона;
- число этих величин;
- вид функциональной зависимости.
П р и м е ч а н и е - Входные величины также могут зависеть от других величин, включая поправки и поправочные коэффициенты на систематические погрешности, поэтому функциональная зависимость может быть сложной и определяемой экспериментально.
А.1.2 Многократные измерения входных величин 
, 
,..., 
;...; 
, 
,..., 
;...; 
, 
,..., 
(
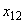1, 2,..., ) позволяют вычислить оценки входных величин, равные
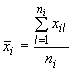, (А.2)
где 
- оценка 
-й входной величины;
- I-й результат измерений -й входной величины;
- число измерений -й входной величины.
А.1.3 Воспроизводимую единицу величины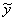 
вычисляют как функцию оценок входных величин 
, 
,..., 
после внесения в показания средств измерений поправок на все известные источники погрешностей, имеющих систематический характер
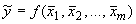. (А.3)
ГОСТ8.381-2009
А.1.4 Оценивание случайной составляющей погрешности
А.1.4.1 Средние квадратические отклонения вычисляют по формулам:
- для ряда результатов измерений входных величин
, (А.4)
- для оценок измеряемых входных величин
. (А.5)
А.1.4.2 В случае некоррелированных оценок , ,..., среднее квадратическое отклонение воспроизводимой единицы величины вычисляют по формуле
. (A.6)
А.1.4.3 В случае коррелированных оценок , ,..., среднее квадратическое отклонение оценки воспроизводимой единицы величины вычисляют по формуле
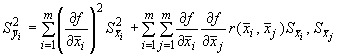, (A.7)
где 
- коэффициент корреляции.
А.1.4.4 Коэффициент корреляции для согласованных пар измерений входных величин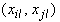 
(I=1, 2,..., 
) вычисляют по формуле
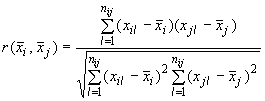, (A.8)
где - число согласованных пар результатов измерений.
ГОСТ8.381-2009
А.1.5 Оценивание неисключенной систематической погрешности
Границу (доверительную границу) НСП оценки воспроизводимой единицы величины 
вычисляют в зависимости от числа оценок входных величин , ,..., , содержащих НСП, и в зависимости от того, представлены ли НСП границами или доверительными границами.
А.1.5.1 Если только одна оценка входной величины из всех оценок входных величин , ,..., содержит НСП, представленную границами 
, границу НСП воспроизводимой единицы величины оценивают по формуле
. (А.9)
А.1.5.2 Если оценки входных величин , ,..., содержат НСП, каждая из которых представлена границами , границу (доверительную границу) , (, 
) НСП воспроизводимой единицы величины оценивают, соответственно, по формулам
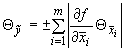, если 
3; (A.10)
, если 
4, (А.11)
где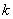 
- коэффициент, определяемый выбранной доверительной вероятностью 
, числом составляющих НСП и их соотношением.
А.1.5.3 Значение коэффициента 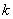для доверительной вероятности , равной 0,99, при числе НСП больше четырех (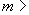
4) принимают равным 1,4 (
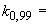1,4), при меньшем числе НСП ( 4) значение коэффициента определяют по графику, приведенному в ГОСТ 8.207.
Для доверительной вероятности , равной 0,95, значение коэффициента 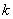равно 1,1 (
1,1).
А.1.5.4 Если оценки I входных величин содержат НСП, представленные границами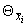 
, а оценки m-I входных величин содержат НСП, представленные доверительными границами, то доверительные границы НСП воспроизводимой
ГОСТ8.381-2009
единицы величины 
оценивают по формуле
, (А.12)
где I - число входных величин, НСП которых представлена границами;
- доверительная граница НСП оценки -й входной величины, вычисленная для доверительной вероятности 
;
, 
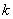- коэффициенты, соответствующие доверительным вероятностям и .
А.1.6 Оценивание доверительных границ суммарной погрешности эталона
А.1.6.1 Доверительные границы суммарной погрешности воспроизводимой единицы величины 
вычисляют по формуле
, (A.13)
где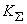 
- коэффициент, определяемый доверительной вероятностью и отношением случайных погрешностей и НСП;
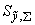- суммарное СКО воспроизводимой единицы величины, обусловленное воздействием случайных погрешностей и НСП.
А.1.6.2 Значение коэффициента 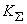вычисляют по формуле
, (A.14)
где - коэффициент Стьюдента, соответствующий доверительной вероятности и эффективному числу степеней свободы 
, вычисляемому по формуле
;
вычисляют по формуле (А.9) или (А.10), или (А.11), или (А.12) в зависимости
ГОСТ8.381-2009
от числа составляющих и формы представления НСП оценок входных величин;
- среднее квадратическое отклонение НСП воспроизводимой единицы величины.
А.1.6.3 Среднее квадратическое отклонение НСП вычисляют, соответственно, по формулам
, (А.15)
если составляющие НСП представлены границами по формуле (А.9) или (А.10);
, (А.16)
если составляющие НСП представлены доверительными границами по формуле (А.11);
. (А.17)
если часть составляющих НСП представлена границами, а часть составляющих НСП - доверительными границами по формуле (А.12),
где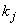 
- коэффициент, соответствующий доверительной вероятности 
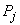при вычислении доверительных границ НСП.
А.1.6.4 Суммарное СКО воспроизводимой единицы величины 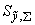, обусловленное воздействием случайных погрешностей и НСП, вычисляют по формуле
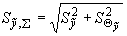. (А.18)
ГОСТ8.381-2009
А.1.7 Значения величин, приписываемых групповому эталону
А.1.7.1 Если различия СКО результатов сличений мер, а также их НСП незначительны, среднее арифметическое значение результатов сличений мер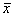 
, входящих в состав группового эталона, вычисляют по формуле
, (А.19)
где - результат сличений -й меры группового эталона;
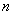- число мер, входящих в состав группового эталона.
А.1.7.2 При значительном различии СКО результатов сличений мер и пренебрежимо малом различии их НСП среднее взвешенное значение результатов сличений мер 
, входящих в состав группового эталона, вычисляют по формуле
, (А.20)
где 
- СКО результата сличений -й меры группового эталона.
А.1.7.3 Если различия СКО, а также НСП результатов сличений мер, входящих в состав группового эталона, существенны, то среднее взвешенное значение результатов сличений мер вычисляют по формуле
, (А.21)
где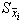 
- СКО результата сличений -й меры группового эталона;
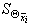- СКО НСП результата сличений -й меры группового эталона.
ГОСТ8.381-2009
А.1.8 Оценивание погрешностей группового эталона
А.1.8.1 Если за значение величины, приписываемое групповому эталону, принимают среднее арифметическое значение мер, входящих в состав группового эталона, то СКО группового эталона вычисляют по формуле
, (А.22)
где - результат сличений -й меры группового эталона.
А.1.8.2 Если за значение величины, приписываемое групповому эталону, принимают среднее взвешенное значение мер, входящих в его состав, то СКО группового эталона 
вычисляют по следующим формулам.
Если различия СКО результатов сличений мер существенны, а различия НСП мер пренебрежимо малы, то формула для расчета имеет вид
. (А.23)
Если различия СКО результатов сличений мер, а также их НСП существенны, то СКО группового эталона вычисляют по формуле
, (А.24)
где 
- СКО НСП результата сличений -й меры группового эталона.
А.2 Оценивание погрешностей воспроизведения производной единицы величины эталоном
А.2.1 Воспроизводимая производная единица величины 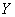зависит от единиц 
, 
,..., 
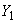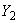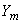, воспроизводимых эталонами, входящими в состав эталона производной единицы величины
. (A.25)
ГОСТ8.381-2009
А.2.2 Воспроизводимая единица величины каждого из эталонов, входящих в состав эталона производной единицы, может зависеть от величин, оказывающих влияние на воспроизводимую единицу и тем самым на производную единицу.
А.2.3 Погрешность воспроизведения производной единицы величины оценивают в соответствии с А.1.4-А.1.6, где вместо погрешностей оценок входных величин , ,..., будут погрешности воспроизводимой производной единицы величины , ,..., .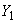
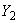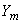А.3 Формулы для оценивания неопределенности измерений при воспроизведении единицы величины эталоном
А.3.1 Воспроизводимая единица величины 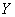в большинстве случаев зависит от других измеряемых входных величин 
, 
,..., 
в соответствии с А.1.1. Воспроизводимую эталоном единицу величины вычисляют в соответствии с А.1.3.
А.3.2 Стандартная неопределенность измерений при воспроизведении единицы величины эталоном, оцениваемая по типу А
Стандартную неопределенность измерений при воспроизведении единицы величины эталоном, оцениваемую по типу А, вычисляют по формуле
, (А.26)
где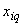 
- 
-й результат измерений -й входной величины;
- число результатов измерений;
- среднее арифметическое значение результатов измерений -й входной величины.
Примечание - При многократных измерениях должна быть обеспечена взаимная независимость отдельных измерений.
А.3.3 Стандартная неопределенность измерений при воспроизведении единицы величины эталоном, оцениваемая по типу В, 
А.3.3.1 Исходные данные для вычисления:
- данные об измерении величин, влияющих на результат измерений входных величин, и данные о зависимости результатов измерений входных величин;
ГОСТ8.381-2009
- данные, полученные в результате опыта о поведении и свойствах приборов и материалов;
- данные о калибровке, поверке, сведения изготовителя о приборе и другие сведения о приборе;
- неопределенности справочных данных, используемых констант.
А.3.3.2 Неопределенности для указанных в А.3.3.1 исходных данных возможно представить только границами (нижней 
и верхней 
), в которых находятся значения измеряемой величины. В случае отсутствия любой информации о значении величины предполагают равномерное распределение возможных ее значений внутри указанного интервала. Например, для -й измеряемой величины нижняя и верхняя границы соответственно равны 
и 
.
Стандартную неопределенность измерений при воспроизведении единицы величины эталоном, оцениваемую по типу В, в подобной ситуации вычисляют по формуле
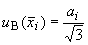, где 
. (А.27)
А.3.3.3 Если интервал от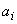 
до 
, несимметричен, то стандартную неопределенность измерений, оцениваемую по типу В, вычисляют по формуле
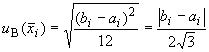. (A.28)
А.3.3.4 Суммарную стандартную неопределенность измерений 
при воспроизведении единицы величины в случае некоррелированных оценок , ,..., вычисляют по формуле
, (A.29)
где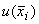 
- стандартная неопределенность измерений -й входной величины, вычисленная по типу А или по типу В.
А.3.3.5 Суммарную стандартную неопределенность измерений в случае коррелированных оценок , ,..., вычисляют по формуле
ГОСТ8.381-2009
, (А.30)
где 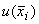- стандартная неопределенность измерений -й входной величины, вычисленная по типу А или по типу В.
Коэффициент корреляции вычисляют в соответствии с А.1.4.4 по формуле (А.8).
А.3.3.6 Расширенную неопределенность измерений 
c выбранным уровнем доверия вычисляют по формуле
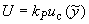, (A.31)
где 
- коэффициент охвата, соответствующий выбранному уровню значимости ;
- суммарная стандартная неопределенность измерений при воспроизведении единицы величины, вычисленная в соответствии с А.3.3.4 или А.3.3.5.
А.3.3.7 Выбор коэффициента охвата требует полного знания распределения вероятностей, которое характеризуется результатом измерений 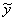и его суммарной стандартной неопределенностью измерений .
А.3.3.8 В общем случае коэффициент охвата выбирают в соответствии с формулой
, (A.32)
где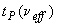 
- квантиль распределения Стьюдента с эффективным числом степеней свободы и уровнем доверия .
Число степеней свободы определяют по формуле
, (А.33)
где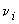 
- число степеней свободы:
ГОСТ8.381-2009
для вычисления неопределенностей измерений по типу А;
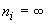для вычисления неопределенностей измерений по типу В.
А.3.3.9 В случае когда распределение результатов измерений не противоречит нормальному, для расчета коэффициента охвата используют квантили нормального распределения:
Расширенную неопределенность измерений при воспроизведении единицы величины эталона 
для уровня доверия 0,99 вычисляют по формуле
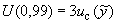. (А.34)
Расширенную неопределенность измерений при воспроизведении единицы величины эталона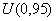 
для уровня доверия 0,95 вычисляют по формуле
. (А.35)
А.4 Значение величины, приписываемое групповому эталону
А.4.1 Если различия стандартных неопределенностей типа А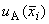 
результатов сличений мер, а также их стандартных неопределенностей типа В 
несущественны, за значение величины, приписываемое групповому эталону, принимают среднее арифметическое значение результатов сличений мер 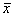, которое вычисляют по формуле
, (А.36)
где - результат сличений -й меры группового эталона;
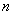- число мер, входящих в состав группового эталона.
А.4.2 При значительном различии стандартных неопределенностей типа А 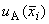результатов сличений мер и пренебрежимо малом различии их стандартных неопределенностей типа В среднее взвешенное значение результатов сличений мер , входящих в состав группового эталона, вычисляют по формуле
ГОСТ8.381-2009
, (А.37)
где 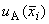- стандартная неопределенность типа А результата сличений -й меры группового эталона.
А.4.3 Если различия стандартных неопределенностей типа А 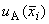результатов сличений мер, а также их стандартных неопределенностей типа В существенны, за значение величины, приписанное групповому эталону, принимают среднее взвешенное значение результатов сличений мер 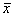, которое вычисляют по формуле
, (А.38)
где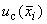 
- суммарное стандартное отклонение -й меры группового эталона.
А.4.4 Если за значение величины, приписываемое групповому эталону, принимают среднее арифметическое значение мер, входящих в состав группового эталона, то стандартную неопределенность типа А 
результатов сличений мер группового эталона вычисляют по формуле
, (А.39)
где - результат сличений -й меры группового эталона.
А.4.5 Если за значение величины, приписываемое групповому эталону, принимают среднее взвешенное значение мер, входящих в его состав, то стандартную неопределенность группового эталона типа А 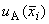вычисляют по следующим формулам.
Если различия стандартных неопределенностей типа А 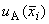результатов сличений мер существенны, а различия стандартных неопределенностей типа В результатов сличений мер пренебрежимо малы, то формула для
ГОСТ8.381-2009
расчета 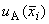имеет вид
. (A.40)
Если различия стандартных неопределенностей типа А 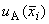результатов сличений мер, а также их стандартных неопределенностей типа В существенны, то 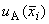группового эталона вычисляют по формуле
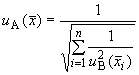, (А.41)
где - стандартная неопределенность типа В результата сличений -й меры группового эталона.
ГОСТ8.381-2009
