
 ,
,
где П — потенциальная энергия точечного заряда q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
Сила, действующая на точечный заряд q, находящийся в электрическом поле, и потенциальная энергия этого заряда

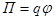 .
.
Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей),
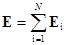

где E i, ji— напряженность и потенциал в данной точке поля, создаваемого i-м зарядом.
Напряженность и потенциал поля, создаваемого точечным зарядом q на расстоянии r

 .
.
Напряженность и потенциал поля, создаваемого проводящей заряженной сферой (с зарядом q) радиусом R на расстоянии r от центра сферы:
a) E=0 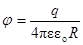 (при r<R),
(при r<R),
б) 
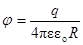 (при r=R),
(при r=R),
в) 
 (при r>R).
(при r>R).
Линейная плотность заряда
 .
.
Поверхностная плотность заряда
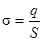 .
.
Напряженность и потенциал поля, создаваемого системой распределенных зарядов, находят, разбивая систему на точечные заряды и используя принцип суперпозиции электрических полей (т.е. проводя интегрирование).
Для расчета электростатических полей сложных заряженных объектов используется также теорема Гаусса:
 (в вакууме),
(в вакууме),
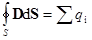 (при наличии диэлектрика),
(при наличии диэлектрика),
где D =eeo E – электрическое смещение, S – замкнутая поверхность, окружающая заряды q i,  и
и 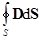 – потоки векторов E и D через поверхность S.
– потоки векторов E и D через поверхность S.
Напряженность поля, создаваемого бесконечной равномерно заряженной прямой линией или бесконечно длинным цилиндром
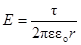 ,
,
где r — расстояние от нити или оси цилиндра до точки, в которой определяется напряженность поля.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью
 .
.
Связь потенциала с напряженностью:
а)  или
или  в общем случае (i,j,k – единичные вектора, направленные вдоль осей X,Y,Z, соответственно);
в общем случае (i,j,k – единичные вектора, направленные вдоль осей X,Y,Z, соответственно);
б) E = (φ 1 – φ 2 )/d в случае однородного поля;
в)  в случае поля, обладающего центральной или осевой симметрией.
в случае поля, обладающего центральной или осевой симметрией.
Электрический момент диполя
 ,
,
где q — заряд, 1 — плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
Момент силы, действующей на диполь во внешнем электрическом поле
 или
или  .
.
Потенциальная энергия диполя во внешнем электрическом поле
 или
или  ,
,
где a– угол между р и Е.
Работа сил поля по перемещению заряда q из точки поля с потенциалом φ 1 в точку с потенциалом φ 2
A 12 = q (φ1 – φ2).
Электроемкость
C = q/ jили C = q/U,
где j — потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U — разность потенциалов пластин конденсатора.
Электроемкость плоского конденсатора
 ,
,
где S — площадь пластины (одной) конденсатора; d — расстояние между пластинами.
Электроемкость батареи N конденсаторов:
а)  — при последовательном соединении;
— при последовательном соединении;
б)  — при параллельном соединении.
— при параллельном соединении.
Энергия заряженного конденсатора:
 ,
,  ,
,  .
.
Сила постоянного тока
 ,
,
где q — заряд, прошедший через поперечное сечение проводника за время t.
Плотность тока
 ,
,
где S — площадь поперечного сечения проводника.
Связь плотности тока со средней скоростью < v >направленного движения заряженных частиц
 ,
,
где q — заряд частицы; п — концентрация заряженных частиц.
Закон Ома:
а)  для однородного участка цепи (не содержащегоЭДС),
для однородного участка цепи (не содержащегоЭДС),
где —j 1 -j 2 =U разность потенциалов (напряжение) на концах участка цепи; R — сопротивление участка;
б)  для неоднородного участка цепи (участка, содержащего ЭДС),
для неоднородного участка цепи (участка, содержащего ЭДС),
где E — ЭДС источника тока; R — полное сопротивление участка (сумма внешних и внутренних сопротивлений);
в)  для замкнутой (полной) цепи,
для замкнутой (полной) цепи,
где R — внешнее сопротивление цепи; r — внутреннее сопротивление цепи.
Правила Кирхгофа:
а)  — первое правило;
— первое правило;
б)  — второе правило,
— второе правило,
где  — алгебраическая сумма сил токов, сходящихся в узле;
— алгебраическая сумма сил токов, сходящихся в узле;  — алгебраическая сумма произведений сил токов на сопротивления участков в замкнутом контуре;
— алгебраическая сумма произведений сил токов на сопротивления участков в замкнутом контуре;  — алгебраическая сумма ЭДС в замкнутом контуре.
— алгебраическая сумма ЭДС в замкнутом контуре.
Сопротивление R и проводимость G проводника
 ,
,  ,
,
где r — удельное электрическое сопротивление; g — удельная электрическая проводимость; l — длина проводника; S — площадь поперечного сечения проводника.
Сопротивление системы проводников:
а) 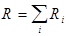 при последовательном соединении;
при последовательном соединении;
б)  при параллельном соединении,
при параллельном соединении,
где R i — сопротивление i-го проводника.
Работа тока:
 .
.
Мощность тока:
 .
.
Закон Джоуля—Ленца
 .
.
Закон Ома в дифференциальной форме
 ,
,
где g — удельная электрическая проводимость; Е — напряженность электрического поля; j — плотность тока.




