Для розв'язання задачі ми будемо використовувати символ 
. Для спрощення розгляду припустимо, що всі цілі числа менше , так що 
для кожного додатнього цілого числа 
та 
. Приймемо також, що 
. Це - для зручності позначень.
Для поліпшення системи позначень використовується наступне визначення.
Визначення. Нехай 
й 
— матриці-рядка, де кожне з 
й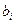 
— ненегативні цілі числа або . Тоді 
.
Визначення. Нехай 
— число, а матриця-
рядок. Тоді 
.
Задача 2. Задано граф. Необхідно визначити найкоротшу відстань між будь-якими двома вершинами графа.
Рішення. Застосуємо алгоритм Флойда-Уоршолла. Нехай 
— матриця, де 
— вага ребра 
якщо ребро існує й у противному випадку. У нашому випадку
.
Знайдемо вагу всіх шляхів довжини 2, або 2-шляхів, у яких середньою вершиною є вершина 
. Починаємо з першого стовпця. Знаходимо перший рядок у першому стовпці, у якій є позитивне ціле число. У цьому випадку це число 2 у другому рядку. Таким чином, існує ребро з вершини 
до вершини . вагою 2. Якщо в першому рядку на позиції 
є ціле число 
, то існує ребро з вершини до вершини 
вагою . Тоді 
— вага 2-шляху з вершини у вершину . Таким чином, якщо додати 2 до кожного елемента в першому рядку, то одержимо рядок, яку варто розглядати як матрицю-рядок, позначаючи її 
, так що 
— вага шляху довжини 2 з вершини до вершини . Якщо розглядати 
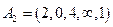, другий рядок матриці як матрицю-рядок, тоді. — вага шляху довжини 1 з вершини до вершини . Оскільки нас цікавить найкоротший шлях для кожного 
, заміняємо другий рядок матриці на 
. Аналогічним образом, у четвертому рядку першого стовпця перебуває число 3, тобто існує ребро з вершини 
- до вершини вагою 3. Якщо в першому рядку на позиції є ціле число , то існує ребро з вершини , до вершини вагою . Тоді 
— вага 2-шляху з вершини до вершини . Отже, якщо додати 3 до кожного елемента в першому рядку, то одержимо рядок, яку варто розглядати як матрицю-рядок, позначаючи її 
, так що 
— вага 2-шляху з к. Якщо розглядати 
четвертий рядок матриці як матрицю-рядок, тоді 
— вага шляхи довжини 1 з к. Оскільки нас цікавить найкоротший шлях для кожного , заміняємо четвертий рядок матриці на 
. І тому що в інших строкаx першого стовпця більше немає позитивних цілих чисел, перший етап завершений, у результаті якого маємо
.
Тепер розглянемо другий стовпець матриці 
. Якщо в 
-тім рядку другого стовпця є число 
, то існує ребро з вершини 
до вершини вагою . Якщо в рядку на позиції 
є ціле число , то існує ребро з вершини до вершини вагою . Тоді 
— вага шляху з к. Отже, якщо додати число до кожного елемента в другому рядку, то одержимо рядок, яку варто розглядати як матрицю-рядок, позначаючи її 
, так що 
— довжина 2-шляху з вершини к. Якщо розглядати 
, -тую рядок матриці як матрицю-рядок, тоді 
— довжина шляхи з вершини к. Оскільки нас цікавить найкоротший шлях для всіх , заміняємо -тую рядок матриці на 
. У другому стовпці є число 2 у першому рядку, число 4 із третьому рядку, число 5 - у четвертому рядку й число 1- у п'ятому рядку. Використовуючи цей процес для кожного з наступних рядків, отримаємо
Розглянемо тепер третій стовпець матриці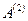 
. Для кожної позиції 
матриці 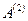на якій є позитивне ціле число, додаємо це число до третього рядка матриці 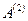, одержуючи матрицю-рядок 
, після чого покладемо 
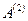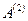рівної -ой рядку матриці . Далі заміняємо -у рядок матриці на 
й одержуємо
.
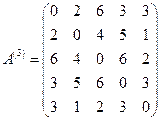Тепер розглянемо четвертий стовпець матриці 
. Для кожного позитивного елемента на позиції 
матриці додаємо це значення до четвертого рядка матриці , щоб одержати 
й покласти рівної -ой рядку матриці . Далі заміняємо -у рядок матриці на 
й одержуємо
.
Нарешті, розглянемо п'ятий стовпець матриці 
. Для кожного позитивного елемента на позиції 
матриці додаємо це значення до п'ятого рядка матриці одержуючи 
й думаємо 
рівної -ой рядку матриці . Далі заміняємо -у рядок матриці на 
одержуємо
.
