ЗМІСТ
Вступ........................................................................................................... 4
1.......................................................................................................................... 5
2.......................................................................................................................... 6
3.......................................................................................................................... 7
4.......................................................................................................................... 8
5........................................................................................................................ 10
Контрольні завдання................................................................................ 20
Список літератури........................................................................................
ВСТУП
Курс дискренної математики є базовим у математичній освіті студентів. Він широко застосовується в різних розділах математики, техніки та природознавства. За допомогою графів зображують системи звязку, розподілу інформації, економічні звязки з підприємствами, послідовність виконання операцій і т.і. Тому круг питань, де використовують графи, надзвичайно широкий.
Дані методичні вказівки призначено для студентів спеціальності “Іінформатика” для вивчення у ІІІ семестрі ІІ модуля “Теорія графів” дисципліни “Дискретна математика”.
Методичні вказівки складено з метою ознайомити студентів з основними поняттями теорії графів, навчити їх самостійно опрацьовувати теоретичний і практичний матеріали, а також допомогти студентам під час виконання контрольних робіт.
Матеріал викладається по темам, які передбачні програмою з дисципліни “Дискретна математика”; наводяться необхідні відомості — основні поняття і твердження, які використовуються при розв’язанні прикладів типових задач.
Методичні вказівки містять також контрольні завдання до теми “Теорія графів”. Студент повинен самостійно розв’язати завдання свого варіантуа, який визначається за номером N в алфавітному списку групи, якщо N >30, то виконується варіант із номером N -30.
Розв’язання завдань із поясненнями подати на скріплених аркушах форматом А4, титульна сторінка роботи оформлюється за зразком, наведеним у додатку А. Кожне завдання необхідно позначити номером за методичними вказівками. Умову завдання треба повністю переписати.
Після перевірки викладачем у разі зауважень студент повинен розв’язати заново неправильно виконані завдання на окремих аркушах, що підшиваються до роботи, і повторно подати його на перевірку. Після позитивної оцінки викладача робота підлягає захисту.
Знаходження найкоротшого шляху між двома вершинами графа
Серед індексних методів розглянемо метод Форда та його інтерпретацію для машинної реалізації - алгоритм Дейкстри.
 |
Задача 1.1. Граф G заданий графічно. Необхідно, використовуючи метод Форда, знайти найкоротшу відстань від вершини х 0 до вершини х 7 і довжину цього ланцюга.
Розв’язання.
1. 
.
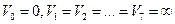2.Розглядаємо всі вершини суміжні з фіксованою і обираємо для розгляду ту, довжина ребра в якій має найшу вагу. Це вершина x 1:
.
3.Далі розглянеио вершину х 2:
Для вершини х 3:
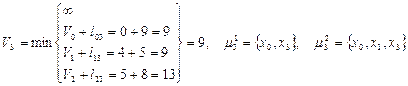Для х5:
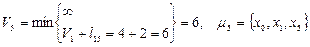
Отже, з вершини х 0 у вершину х 7 існують три найкоротші шляхи, довжина яких дорівнює 18.
Задача 1.2. Знайдемо розвязання попереднього прикладу алгоритмом Дейкстри.
Розв’язання.Запишемо вихідні дані у матричному вигляді. Побудуємо матрицю суміжності ваг 
.
Кожний крок відповідає побудові трьох векторів розмірності n, де n - кількість вершин графа:
А- логічний вектор, елемент а і=1, якщо вершина х і розглянута (на початку це вершина відправлення х 0) і а і=0, якщо не розглянута;
В - поточне значення індексів вершин графа, тобто довжина найкоротших шляхів між вершинами х0 та х і (на початку елементи вектора В відповідають нульовому рядку матриці Д, оскільки вершина х 0 є початковою, за винятком елемента в 0, який дорівнює 0);
С - містить номери попередніх вершин,тобто с і – номер вершини, яка стоїть перед і -у у найкоротшому шляху в і -ту вершину (на початку всі елементи с і=0, оскільки початкова вершина х 0).
Серед елементів ві вибираємо найменший для нерозглянутих вершин (яким відповідає а і=0). Це елемент в 1=4.
| і | ||||||||
| Аі | ||||||||
| Ві | ¥ | ¥ | ¥ | ¥ | ||||
| Сі |
Таким чином вершина 1 стає поточною і головною для виконання всіх перетворень даного кроку.
Виконуємо такі перетворення:
а1=1;
для кожного елемента ві, який відповідає аі=0, перевіряємо наявність більш короткого шляху в і-ту вершину з 0-ї через першу, тобто перевіряємо умову ві<в1+д1і. У разі її невиконання замінюємо існуюче значення ві на в1+д1і, а існуюче сі - на 1.
Для елементів в2 та в3 співпадають значення, що порівнюються, тому елементам с2 та с3 припишемо два значення 0,1.
| і | Знову серед елементів ві вибираємо найменший для нерозглянутих вершин (яким відповідає аі=0). Це елемент в2=5. Вершина 2 – поточна. | |||||||||||
| Аі | ||||||||||||
| Ві | 5 | ¥ | ¥ | ¥ | ||||||||
| Сі | 0,1 | 0,1 | ||||||||||
| 2-й єтап | Поточна вершина 5. | |||||||||||
| Аі | ||||||||||||
| Ві | ¥ | 6 | ¥ | |||||||||
| Сі | 0,1 | 0,1 | ||||||||||
| 3-й єтап | Поточна вершина 5. | |||||||||||
| Аі | ||||||||||||
| Ві | 9 | |||||||||||
| Сі | 0,1 | 0,1 | 2,5 | |||||||||
| 4-й єтап | Поточна вершина 4. | |||||||||||
| Аі | ||||||||||||
| Ві | 14 | |||||||||||
| Сі | 0,1 | 0,1 | 2,5 | |||||||||
| 5-й єтап | Поточна вершина 6. | |||||||||||
| Аі | ||||||||||||
| Ві | 16 | |||||||||||
| Сі | 0,1 | 0,1 | 2,5 | |||||||||
| 6-й єтап | Для розгляду залишилась одна вершина х7. Її вибір не змінить отриманих результатів, тобто алгоритм перерахунку завершено. | |||||||||||
| Аі | ||||||||||||
| Ві | ||||||||||||
| Сі | 0,1 | 0,1 | 2,5 | |||||||||
Остання таблиця містить інформацію про довжину найкоротшого шляху від початкової вершини х 0 до будь-якої х і. Сам шлях можна відтворити за елементами вектора С. Випишемо результат для вершини х 7.
