С 2.1. (Бур 388) Две перпендикулярные прямые, проходящие через точку M, пересекают окружность в точках A,B и C,D.
Доказать, что 
.
С 2.2. (Бек 1.13) В параллелограмме ABCD точка K – середина отрезка BC, а точка O – точка пересечения диагоналей. Принимая за базисные векторы 
и 
, найти в этом базисе координаты векторов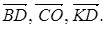 
С 2.3. (Бек 1.18) Дан правильный шестиугольник ABCDEF. Принимая за базисные векторы 
и 
найти в этом базисе координаты векторов 
С 2.4. (Бек 1.26) Дан правильный шестиугольник ABCDEF. Принимая за начало координат вершину A, а за базисные векторы и 
найти координаты вершин шестиугольника и его центра.
С 2.5. (Бек 1.27) В трапеции ABCD отношение длин оснований AD и BC равно 4. Принимая за начало координат вершину A, а за базисные векторы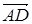 
и 
найти координаты вершин трапеции, точки M пересечения ее диагоналей и точки S пересечения продолжений боковых сторон.
С 2.6. (Бек 1.28) Дан параллелепипед ABCDA 1 B 1 C 1 D 1. Принимая за начало координат вершину A, а за базисные векторы 
найти координаты
1) вершин C, B 1 и C 1;
2) точек K и L – середин ребер A 1 B 1 и CC 1 соответственно;
3) точек M и N пересечения диагоналей граней A 1 B 1 C 1 D 1 и ABB 1 A 1 соответственно;
4) точки O пересечения диагоналей параллелепипеда.
С 2.7. (Мод 1) Векторы 
= a и 
= b служат диагоналями параллелограмма ABCD. Выразить векторы 
через векторы a и b.
С 2.8. (Мод 4-5) В треугольнике ABC проведены медианы AD, BE, CF. Представить векторы 
в виде линейных комбинаций векторов 
. Найти сумму векторов 
С 2.9. (Мод 8) Точки K и L служат серединами сторон 
и 
параллелограмма ABCD. Выразить векторы 
через векторы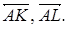 
С 2.10. (Мод 9) В плоскости треугольника ABC найти такую точку M, что сумма векторов 
равна нулю. Указание. Выразить радиус-вектор 
через радиус-векторы 
С 2.11. (Доп) Докажите, что точка M из задачи 2.10 является точкой пересечения медиан треугольника ABC.
С 2.12. (Бур 380) Существует ли в плоскости треугольника ABC такая точка M, что сумма векторов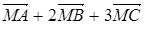 
= 0.
С 2.13. (Доп) В тетраэдре ABCD найти такую точку M, что сумма векторов 
равна нулю. Указание. Выразить радиус-вектор через радиус-векторы 
С 2.14. (Доп) Медианой тетраэдра ABCD называется отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани. Доказать, что все четыре медианы тетраэдра пересекаются в одной точке и делятся в этой точке в отношении 3: 1, считая от вершины. Указание. Эта точка совпадает с точкой M из задачи2.14.
С 2.15. (Мод 90) Один из концов отрезка AB находится в точке A (2,3), его серединой служит точка M (1,–2). Найти другой конец отрезка.
С 2.16. (Мод 91) Даны середины сторон треугольника (2,4), (–3,0), (2,1). Найти его вершины.
С 2.17. (Кле 109) Точка M пересечения медиан треугольника лежит на оси абсцисс, две вершины треугольника – точки A (2,–3) и B (–5,1), третья вершина C лежит на оси ординат. Найти точки M и C.
С 2.18. (Мод 92) Даны две смежные вершины параллелограмма ABCD:
A (–4,–7), B (2,6) и точка пересечения диагоналей M (3,1). Найти две другие вершины параллелограмма.
С 2.20. (Мод 110) Найти отношение, в котором плоскость Oyz делит отрезок AB, если A (2,–1,7), B (4,5,–2).
С 2.21. (Кле 742) Определить координаты концов отрезка, который точками C (2,0,2) и
D (5,–2,0) разделен на три равные части.
С 2.22. (Доп) Найти координаты центра тяжести однородной пластинки, имеющей форму прямоугольной трапеции (рис. 2.7).
