УЧЕБНЫЕ МАТЕРИАЛЫ
Для студентов заочной формы обучения
по дисциплине Теория вероятностей и математическая статистика
для направления подготовки 38.03.01 Экономика
Общая трудоемкость дисциплины
| Виды занятий | Распределение по семестрам в часах | Всего часов |
| семестр | ||
| Общая трудоемкость | ||
| Аудиторные занятия, в т.ч.: | ||
| лекционные (ЛК) | ||
| практические (семинарские) (ПЗ) | ||
| лабораторные (ЛР) | - | - |
| Самостоятельная работа студентов (СРС) | ||
| Форма промежуточного контроля в семестре | экзамен |
Краткое содержание курса
Семестр
1. Предмет теории вероятностей. Понятие случайного события. Классическое и геометрическое определение вероятности. Комбинаторика. Элементарная теория вероятностей. Методы вычисления вероятностей. Теоремы сложения и умножения вероятностей.
2. Условные вероятности. Независимые события и правило умножения вероятностей. Полная группа событий. Формула полной вероятности. Формула Байеса.
3. Схема повторных независимых испытаний (схема Бернулли). Формула Бернулли. Наиболее вероятное число успехов в схеме Бернулли. Приближенные формулы Лапласа и Пуассона.
4. Случайная величина как функция на пространстве элементарных событий. Функция распределения случайной величины. Свойства функции распределения. Независимость случайных величин. Функции от одной или нескольких случайных величин. Дискретная случайная величина (ДСВ) и ее закон распределения.
5. Основные числовые характеристики ДСВ: математическое ожидание, дисперсия, стандартное отклонение, ковариация и коэффициент корреляции. Математическое ожидание функции от ДСВ.
6. Биномиальный закон распределения. Закон распределения Пуассона. Геометрическое распределение. Равномерный закон распределения. Показательный закон распределения. Нормальный закон распределения.
7. Предмет математической статистики. Вариационные ряды и их графическое изображение. Эмпирическая функция распределения. Средние величины Упрощенный способ расчета средней арифметической и дисперсии. Оценка неизвестных параметров. Методы нахождения точечных оценок. Понятие интервального оценивания параметров. Доверительные интервалы для параметров нормального распределения. Проверка статистических гипотез.
Форма текущего контроля
Основной формой обучения студента заочной формы обучения является самостоятельная работа над учебным материалом, включающая чтение учебников, решение задач, выполнение контрольных заданий.
После изучения перечисленных разделов студент должен выполнить контрольную работу по варианту, выбранному по первой букве фамилии из таблицы.
Правила выполнения контрольной работы:
1. Контрольная работа должна быть выполнена в отдельной тетради в клетку (18листов) пастой любого цвета, кроме красного и зеленого в рукописном виде. Набранная на компьютере контрольная работа не рассматривается. Необходимо оставлять поля шириной 4-5 см для замечаний преподавателя.
2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины, здесь же следует указать название учебного заведения, дату отсылки работы. В конце работы следует поставить дату выполнения и подпись студента.
3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту контрольной работы. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются.
4. Решение задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи надо полностью выписать ее условие.
6. Контрольная работа должна выполняться самостоятельно. Несамостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по изучаемой теме. Если преподаватель установит несамостоятельное выполнение работы, а именно, студент не сможет ответить на вопросы преподавателя по решению задач контрольной работы, то она не будет зачтена, даже если в этой работе все задачи решены, верно.
7. Получив от преподавателя прорецензированную работу (как зачтенную, так и не зачтенную), студент должен исправить все отмеченные рецензентом ошибки и недочеты. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
8. Контрольная работа сдается на кафедру ПИМ за месяц до начала сессии.
Задания к контрольной работе
| Вариант | Контрольная работа |
| А, Л, Х | №1 № 11 № 21 № 31 №41 |
| Б, М, Ц | №2 № 12 № 22 №32 №42 |
| В, Н, Ч | №3 №13 № 23 № 33 №43 |
| Г, О, Ш | №4 №14 №24 № 34 №44 |
| Д, П, Щ | №5 №15 № 25 № 35 №45 |
| Е, Е, Р, Ы | №6 № 16 № 26 №36 №46 |
| Ж, С, Э | №7 №17 №27 №37 №47 |
| З, Т, Ю | №8 №18 №28 №38 №48 |
| И, Й, У | №9 №19 №29 №39 №49 |
| К, Ф, Я | №10 №20 №30 №40 №50 |
1–10.
1.В контейнере находятся 40 телевизоров, среди которых 5 имеют скрытые дефекты. Найти вероятность того, что 3 наудачу выбранных телевизора не будут иметь дефектов.
2. Автомат изготавливает однотипные детали, причем технология изготовления такова, что 5% произведенной продукции оказывается бракованной. Найти вероятность того, что из четырех наугад взятых деталей будут бракованными не более двух деталей.
3. На склад поступают однотипные детали с двух заводов – №1 и №2. Завод №1 поставляет 30% деталей, из которых 10% имеют низкое качество. Завод №2 производит детали, из которых 80% имеют высокое качество. Найти вероятность того, что наугад взятая со склада деталь будет высокого качества.
4. Два оператора набили по одинаковому комплекту перфокарт. Вероятность того, что первый оператор допустит ошибку, равна 0,1; для второго оператора эта вероятность равна 0,2. При сверке перфокарт была обнаружена ошибка. Какова вероятность того, что ошибся первый оператор?
5. Предприятие состоит из трех независимо работающих подразделений. Предполагается, что вероятность их рентабельной работы в течение времени  соответственно равна 0,6; 0,7 и 0,8. Найти вероятность того, что в течение времени
соответственно равна 0,6; 0,7 и 0,8. Найти вероятность того, что в течение времени  рентабельными будут: а) все подразделения, б) два подразделения.
рентабельными будут: а) все подразделения, б) два подразделения.
6. Студенту для сдачи зачета по теории вероятностей предлагается 3 вопроса, для каждого вопроса предлагается 5 различных ответов, из которых только один верный. Какова вероятность успешной сдачи зачета при выборе ответов наугад?
7. Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для третьего – 0,9. Найти вероятность того, что: 1) все три стрелка попадут в цель; 2) все трое промахнутся; 4) хотя бы один стрелок попадет в цель.
8. Из 20 экзаменационных билетов 3 содержат простые вопросы. Пять студентов по очереди берут билеты. Найти вероятность того, что хотя бы одному из них достанется билет с простыми вопросами.
9. В каждом из двух ящиков содержатся 6 черных и 4 белых шара. Из первого ящика наудачу переложили во второй ящик 1 шар. Найти вероятность того, что два наугад взятые шара из второго ящика будут белыми.
10. Вероятность поражения стрелком мишени при одном выстреле равна 0,8. Найти вероятность того, что при пяти последовательных выстрелах будет не менее четырех попаданий.
11–20.
Задана плотность распределения вероятностей  непрерывной случайной величины Х. Требуется:
непрерывной случайной величины Х. Требуется:
1) определить коэффициент А;
2) найти функцию распределения  ;
;
3) схематично построить графики  и
и  ;
;
4) найти математическое ожидание и дисперсию Х;
5) найти вероятность того, что Х примет значение из интервала  .
.
11.  12.
12. 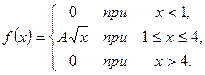


13.  14.
14. 


15.  16.
16. 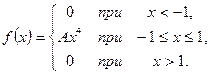


17.  18.
18. 


19.  20.
20. 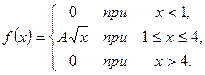


21–30.
Заданы математическое ожидание  и среднее квадратическое отклонение
и среднее квадратическое отклонение  нормально распределенной случайной величины Х. Требуется:1) написать плотность распределения вероятностей
нормально распределенной случайной величины Х. Требуется:1) написать плотность распределения вероятностей  и схематично построить ее график;2) найти вероятность того, что Х примет значение из интервала
и схематично построить ее график;2) найти вероятность того, что Х примет значение из интервала  .
.
| 21. |  1, 1,
|  5, 5,
|  0.5, 0.5,
|  3. 3.
| 22. |  9, 9,
|  5, 5,
|  2, 2,
|  8. 8.
|
| 23. |  2, 2,
|  4, 4,
|  1, 1,
|  5. 5.
| 24. |  8, 8,
|  3, 3,
|  1, 1,
|  6. 6.
|
| 25. |  3, 3,
|  2, 2,
|  2, 2,
|  8. 8.
| 26. |  6, 6,
|  4, 4,
|  0, 0,
|  5. 5.
|
| 27. |  4, 4,
|  4, 4,
|  3, 3,
|  6. 6.
| 28. |  4, 4,
|  6, 6,
|  5, 5,
|  9. 9.
|
| 29. |  5, 5,
|  6, 6,
|  4, 4,
|  9. 9.
| 30. |  2, 2,
|  3, 3,
|  4, 4,
|  8. 8.
|
31–40.
Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью 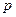 . Опыт повторяют в неизменных условиях
. Опыт повторяют в неизменных условиях  раз.
раз.
31.  . Определить вероятность того, что в 900 опытах событие А произойдет от 250 до 320 раз.
. Определить вероятность того, что в 900 опытах событие А произойдет от 250 до 320 раз.
32.  . Определить вероятность того, что относительная частота появления события А отклонится от
. Определить вероятность того, что относительная частота появления события А отклонится от  не более чем на 0,05.
не более чем на 0,05.
33.  . Определить вероятность того, что в 1000 опытах событие А произойдёт не менее чем 580 раз.
. Определить вероятность того, что в 1000 опытах событие А произойдёт не менее чем 580 раз.
34.  . Определить вероятность того, что в 700 опытах событие А произойдёт в меньшинстве опытов.
. Определить вероятность того, что в 700 опытах событие А произойдёт в меньшинстве опытов.
35.  . Определить вероятность того, что в 900 опытах событие А произойдёт в большинстве опытов.
. Определить вероятность того, что в 900 опытах событие А произойдёт в большинстве опытов.
36.  . Определить вероятность того, что в 800 опытах относительная частота появления события А отклонится от вероятности
. Определить вероятность того, что в 800 опытах относительная частота появления события А отклонится от вероятности 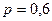 не более чем на 0,05.
не более чем на 0,05.
37.  . Найти, какое отклонение относительной частоты появления события А от
. Найти, какое отклонение относительной частоты появления события А от  можно ожидать с вероятностью 0,9.
можно ожидать с вероятностью 0,9.
38. 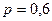 . Определить сколько раз
. Определить сколько раз  надо провести опыт, чтобы с вероятностью большей, чем 0,9 можно было ожидать отклонения относительной частоты появления события А от
надо провести опыт, чтобы с вероятностью большей, чем 0,9 можно было ожидать отклонения относительной частоты появления события А от 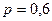 не более чем 0,05.
не более чем 0,05.
39.  . Найти вероятность того, что относительная частота появления события А отклонится от
. Найти вероятность того, что относительная частота появления события А отклонится от  не более чем на 0,1.
не более чем на 0,1.
40.  . Определить вероятность того, что в 800 опытах событие А произойдет от 300 до 400 раз.
. Определить вероятность того, что в 800 опытах событие А произойдет от 300 до 400 раз.
41-50.
В результате эксперимента получены данные, записанные в виде статистического ряда. В задачах требуется: А) записать значения результатов экспериментов в виде вариационного ряда; Б) найти размах варьирования и разбить его на 9 интервалов; В) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения; Г) найти числовые характеристики выборки  ;Д) приняв в качестве нулевой гипотезу Н0: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить ее, пользуясь критерием Пирсона при уровне значимости
;Д) приняв в качестве нулевой гипотезу Н0: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить ее, пользуясь критерием Пирсона при уровне значимости  ;Е) найти доверительный интервал для математического ожидания при надежности
;Е) найти доверительный интервал для математического ожидания при надежности 
41.
| 17,1 | 21,4 | 15,9 | 19,1 | 22,4 | 20,7 | 17,9 | 18,6 | 21,8 | 16,1 |
| 19,1 | 20,5 | 14,2 | 16,9 | 17,8 | 18,1 | 19,1 | 15,8 | 18,8 | 17,2 |
| 16,2 | 17,3 | 22,5 | 19,9 | 21,1 | 15,1 | 17,7 | 19,8 | 14,9 | 20,5 |
| 17,5 | 19,2 | 18,5 | 15,7 | 14,0 | 18,6 | 21,2 | 16,8 | 19,3 | 17,8 |
| 18,8 | 14,3 | 17,1 | 19,5 | 16,3 | 20,3 | 17,9 | 23,0 | 17,2 | 15,2 |
| 15,6 | 17,4 | 21,3 | 22,1 | 20,1 | 14,5 | 19,3 | 18,4 | 16,7 | 18,2 |
| 18,4 | 18,7 | 14,3 | 18,2 | 19,1 | 15,3 | 21,5 | 17,2 | 22,6 | 20,4 |
| 22,8 | 17,5 | 20,2 | 15,5 | 21,6 | 18,1 | 20,5 | 14,0 | 18,9 | 16,5 |
| 20,8 | 16,5 | 18,3 | 21,7 | 17,4 | 23,0 | 21,1 | 19,8 | 15,4 | 18,1 |
| 18,9 | 14,7 | 19,5 | 20,9 | 15,8 | 20,2 | 21,8 | 18,2 | 21,2 | 20,1 |
42.
| 16,8 | 17,9 | 21,4 | 14,1 | 19,1 | 18,1 | 15,1 | 18,2 | 20,3 | 16,7 |
| 19,5 | 18,5 | 22,5 | 18,4 | 16,2 | 18,1 | 19,1 | 21,4 | 14,5 | 16,1 |
| 21,5 | 14,9 | 18,6 | 20,4 | 15,2 | 18,5 | 17,1 | 22,4 | 20,8 | 19,8 |
| 17,2 | 19,7 | 16,3 | 18,7 | 14,4 | 18,8 | 19,5 | 21,6 | 15,3 | 17,3 |
| 22,8 | 17,4 | 22,7 | 16,5 | 21,7 | 15,4 | 21,3 | 14,3 | 20,5 | 16,4 |
| 20,6 | 15,5 | 19,4 | 17,5 | 20,9 | 23,0 | 18,9 | 15,9 | 18,2 | 20,7 |
| 17,9 | 21,8 | 14,2 | 21,2 | 16,1 | 18,4 | 17,5 | 19,3 | 22,7 | 19,6 |
| 22,1 | 17,6 | 16,7 | 20,4 | 15,7 | 18,1 | 16,6 | 18,3 | 15,5 | 17,7 |
| 19,2 | 14,8 | 19,7 | 17,7 | 16,5 | 17,8 | 18,5 | 14,0 | 21,9 | 16,9 |
| 15,8 | 20,8 | 17,1 | 20,1 | 22,6 | 18,9 | 15,6 | 21,1 | 20,2 | 15,1 |
4 3.
4 4.
| 9,4 | 7,9 | 6,3 | 6,8 | 4,2 | 11,9 | 7,8 | 1,7 | 6,1 | 8,8 |
| 8,7 | 11,1 | 7,7 | 1,8 | 5,5 | 10,5 | 4,3 | 3,8 | 1,4 | 11,2 |
| 1,1 | 7,3 | 3,7 | 4,4 | 11,8 | 8,6 | 1,9 | 5,6 | 10,1 | 8,4 |
| 10,0 | 11,6 | 5,2 | 2,1 | 5,7 | 4,8 | 7,4 | 0,8 | 4,7 | 3,6 |
| 8,3 | 7,6 | 0,7 | 7,3 | 3,4 | 11,4 | 5,7 | 9,9 | 2,2 | 4,6 |
| 2,3 | 4,7 | 9,7 | 11,3 | 5,8 | 4,9 | 3,3 | 0,5 | 7,5 | 4,6 |
| 5,0 | 0,4 | 8,9 | 7,1 | 9,6 | 11,5 | 5,9 | 9,0 | 5,3 | 2,4 |
| 9,5 | 5,9 | 1,0 | 9,1 | 2,5 | 6,0 | 8,2 | 3,2 | 10,9 | 6,1 |
| 10,2 | 2,6 | 4,5 | 3,1 | 6,2 | 11,7 | 6,3 | 0,2 | 7,0 | 9,2 |
| 1,2 | 6,4 | 11,9 | 6,9 | 8,1 | 6,5 | 2,9 | 6,2 | 4,4 | 10,3 |
4 5.
| 1,6 | 4,4 | 10,9 | 6,4 | 4,0 | 2,8 | 5,2 | 1,2 | 7,6 | 3,4 |
| 2,9 | 5,3 | 1,7 | 7,7 | 6,9 | 10,1 | 5,4 | 4,1 | 8,8 | 6,5 |
| 6,6 | 4,2 | 5,5 | 0,5 | 8,9 | 4,5 | 1,8 | 5,6 | 7,8 | 3,0 |
| 1,9 | 10,2 | 7,9 | 2,5 | 5,7 | 3,1 | 6,7 | 4,3 | 0,6 | 9,0 |
| 6,8 | 3,2 | 4,4 | 9,1 | 10,3 | 6,0 | 7,9 | 6,9 | 8,0 | 2,0 |
| 7,0 | 10,7 | 8,1 | 2,1 | 5,8 | 6,4 | 0,3 | 4,5 | 9,2 | 3,3 |
| 7,6 | 9,3 | 3,4 | 4,6 | 5,0 | 3,8 | 5,9 | 8,2 | 2,2 | 7,1 |
| 2,3 | 0,8 | 7,2 | 8,3 | 11,1 | 6,5 | 3,5 | 9,4 | 10,8 | 4,7 |
| 4,8 | 6,1 | 3,6 | 9,5 | 8,4 | 2,4 | 6,3 | 7,3 | 5,7 | 0,9 |
| 7,4 | 8,5 | 5,8 | 1,1 | 5,9 | 4,9 | 3,7 | 9,6 | 2,6 | 6,1 |
4 6.
47.
48.
4 9.
50.
| 57,3 | 75,1 | 78,1 | 69,3 | 60,1 | 77,3 | 66,1 | 69,5 | 72,1 | 68,7 |
| 81,1 | 69,4 | 63,1 | 67,4 | 77,1 | 82,6 | 64,8 | 72,5 | 62,5 | 80,7 |
| 77,6 | 65,8 | 78,3 | 57,7 | 80,7 | 64,4 | 72,8 | 67,3 | 83,1 | 70,6 |
| 75,3 | 58,0 | 60,7 | 81,3 | 67,1 | 69,6 | 82,4 | 62,3 | 66,9 | 80,6 |
| 62,7 | 73,8 | 68,9 | 83,8 | 57,0 | 72,6 | 65,6 | 78,7 | 59,5 | 70,0 |
| 73,5 | 58,1 | 64,0 | 83,9 | 84,0 | 63,5 | 74,1 | 77,7 | 68,5 | 80,5 |
| 66,3 | 73,0 | 79,1 | 71,1 | 80,4 | 62,1 | 66,7 | 83,7 | 76,8 | 59,3 |
| 71,3 | 63,7 | 71,2 | 78,9 | 65,2 | 77,9 | 74,9 | 69,1 | 70,8 | 74,8 |
| 71,6 | 72,9 | 61,9 | 71,5 | 75,4 | 71,7 | 59,9 | 74,3 | 76,1 | 70,9 |
| 61,3 | 71,4 | 71,8 | 65,0 | 67,8 | 75,5 | 71,9 | 64,9 | 74,7 | 62,9 |






