1)  на отрезке на отрезке 
| 2)  на отрезке на отрезке 
|
Задача №3
Найти экстремумы и интервалы монотонности функций.
1) 
|
2) 
|
3) 
|
4) 
|
5) 
|
Задача №4
Найти асимптоты следующих кривых.
1) 
|
2) 
|
3) 
|
4) 
|
Задача №5
Найти точки перегиба и интервалы выпуклости функций.
1) 
|
2) 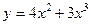
|
3) 
|
4) 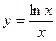
|
Задача №6
Построить графики функций.
1) 
| 2) 
|
Задача №7
Найти частные производные  и
и  следующих функций.
следующих функций.
1) 
|
2) 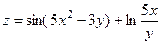
|
3) 
|
Задача №8
Найти в точке A градиент функции  и производную по направлению вектора
и производную по направлению вектора  .
.
1)  
| 2)  
|
Задача №9
Найти экстремумы функции двух переменных: 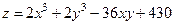
Решение задачи №1
Сначала находим производную  в произвольной точке
в произвольной точке 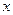 , а затем производим вычисления в конкретной точке
, а затем производим вычисления в конкретной точке 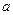 , соблюдая следующий порядок действий:
, соблюдая следующий порядок действий:
- находим значение
 ;
;
- находим производную
 ;
; - подставляя найденные значения в уравнения касательной и нормали (20) и (21), получаем нужные уравнения касательной и нормали.
1) Имеем:  .
.
Для точки с абсциссой в точке  находим:
находим:
-
 ;
; -
 ;
; -


 – уравнение касательной;
– уравнение касательной;


 – уравнение нормали.
– уравнение нормали.
Для точки с абсциссой в точке  находим:
находим:
-
 ;
; -
 ;
; -


 – уравнение касательной;
– уравнение касательной;


 – уравнение нормали.
– уравнение нормали.
Для точки с абсциссой в точке  находим:
находим:
-
 ;
; -
 ;
; -
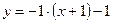

 – уравнение касательной;
– уравнение касательной;


 – уравнение нормали.
– уравнение нормали.
2) Имеем:  .
.
Для точки с абсциссой в точке  находим:
находим:
-
 ;
; -
 ;
; -


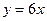 – уравнение касательной;
– уравнение касательной;


 – уравнение нормали.
– уравнение нормали.
Для точки с абсциссой в точке  находим:
находим:
-
 ;
; -
 ;
; -
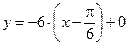

 – уравнение касательной;
– уравнение касательной;


 – уравнение нормали.
– уравнение нормали.
Для точки с абсциссой в точке  находим:
находим:
-
 ;
; -
 ;
; -


 – уравнение касательной;
– уравнение касательной;


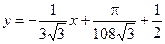 – уравнение нормали.
– уравнение нормали.
Решение задачи №2
Наибольшее и наименьшее значения непрерывной функции  на данном отрезке
на данном отрезке 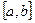 могут достигаться в критических точках функции (т.е. в точках, в которых
могут достигаться в критических точках функции (т.е. в точках, в которых  или
или  не существует) или на концах отрезка
не существует) или на концах отрезка 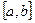 . Порядок действий таков:
. Порядок действий таков:
- проверяем, что заданная функция на данном отрезке является непрерывной;
- ищем производную заданной функции (там, где она существует);
- находим критические точки функции
 и выбираем из них те, которые принадлежат интервалу
и выбираем из них те, которые принадлежат интервалу  ;
; - вычисляем значения функции в критических точках внутри отрезка и значения функции на концах отрезка; сравнивая полученные значения, находим наибольшее и наименьшее значения функции на
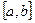 .
.
1) Рассмотрим функцию  на отрезке
на отрезке  .
.
· Заданная функция является многочленом, а многочлен имеет производную в каждой точке прямой. По лемме 3 из лекции 6 данная функция непрерывна на отрезке  .
.
· Вычисляем производную функции:  .
.
· Находим критические точки: 



 . Данному отрезку
. Данному отрезку  принадлежит только точка
принадлежит только точка  .
.
· Вычисляем значение функции в точке  и значения функции на концах заданного отрезка. Имеем:
и значения функции на концах заданного отрезка. Имеем:
 ,
,  ,
,  .
.
Сравнивая эти значения, заключаем, что наименьшее значение функции достигается в точке  и оно равно
и оно равно  , а наибольшее значение функции достигается в точке
, а наибольшее значение функции достигается в точке  и оно равно 27.
и оно равно 27.
2) Рассмотрим функцию  на отрезке
на отрезке  .
.
· Заданная функция является дробно-рациональной функцией, которая дифференцируема во всех точках, в которых знаменатель неравен нулю. Знаменатель обращается в нуль в точке 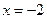 , которая не принадлежит отрезку
, которая не принадлежит отрезку  . По лемме 3 из лекции 6 данная функция непрерывна на отрезке
. По лемме 3 из лекции 6 данная функция непрерывна на отрезке  .
.
· Вычисляем производную функции:  .
.
· Так как  , то критических точек нет.
, то критических точек нет.
· наибольшее и наименьшее значения функции достигаются в граничных точках отрезка:  ;
;  .
.
Решение задачи №3
План исследования функции на экстремум с помощью первой производной таков:
- находим область определения функции
 ;
; - находим
 ;
; - находим критические точки функции
 (то есть те точки, в которых
(то есть те точки, в которых  или
или  не существует); пусть этими точками будут точки с абсциссами
не существует); пусть этими точками будут точки с абсциссами  , которые расположены в порядке их возрастания;
, которые расположены в порядке их возрастания; - разбиваем
 критическими точками на интервалы и внутри каждого интервала методом пробных точек находим знак
критическими точками на интервалы и внутри каждого интервала методом пробных точек находим знак  ; все действия оформляем в виде таблицы (см. примеры 21–25 из лекции 8);
; все действия оформляем в виде таблицы (см. примеры 21–25 из лекции 8); - используя теоремы 17 и 18 из лекции 8, определяем, на каких интервалах данная функция возрастает, на каких убывает, а также находим точки локального экстремума.
1) Рассмотрим функцию  .
.
· Очевидно, что 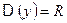 .
.
· Производная существует на всей числовой оси. Вычисляем:  .
.
· Решаем уравнение  :
: 



 ,
,  – критические точки.
– критические точки.
· Все дальнейшие действия оформляем в виде таблицы:
| 
| 
| 
| ||

| – | – | + | ||

| 
| 
| 
| 
| |
| нет extr | min

|
Первая строка – это область определения функции, раздробленная на интервалы критическими точками. Выберем внутри каждого из этих интервалов произвольную точку и определим в этой точке знак первой производной  . В интервале
. В интервале  возьмем, например, точку
возьмем, например, точку  и получаем
и получаем  ; в интервале
; в интервале  возьмем точку
возьмем точку  и получаем
и получаем  ; в интервале
; в интервале  возьмем точку
возьмем точку 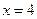 и получаем
и получаем  (вместо этих точек в каждом из интервалов можно взять любые другие точки – результат будет тот же самый). Полученную информацию заносим во вторую строку таблицы.
(вместо этих точек в каждом из интервалов можно взять любые другие точки – результат будет тот же самый). Полученную информацию заносим во вторую строку таблицы.
- Применяя теорему 17, заключаем, что на интервалах
 и
и  функция строго монотонно убывает, а на интервале
функция строго монотонно убывает, а на интервале  – строго монотонно возрастает. Используя теорему 18, приходим к заключению, что в критической точке
– строго монотонно возрастает. Используя теорему 18, приходим к заключению, что в критической точке  экстремума нет (как убывала функция до этой точки, так и убывает после нее); в критической точке
экстремума нет (как убывала функция до этой точки, так и убывает после нее); в критической точке  имеем локальный минимум. Полученные результаты заносим в третью и четвертую строки таблицы.
имеем локальный минимум. Полученные результаты заносим в третью и четвертую строки таблицы.
2) Рассмотрим функцию  .
.
-
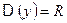 .
. -
 .
. -
 :
: 



 ,
,  .
. - Составляем таблицу:
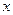
| 
| 
| 
| 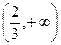
| |

| – | + | – | ||

| 
| 
| 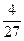
|  
| |
min

| max

|
Ясно, что  – точка минимума, а
– точка минимума, а  ;
;  – точка максимума, причем
– точка максимума, причем 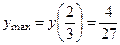 .
.
3) Рассмотрим функцию  .
.
-
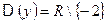 .
. -
 .
. -




 ,
,  – критические точки.
– критические точки. - Строим таблицу:
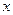
| 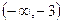
| –3 | 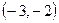
| 
| 
| 
|

| – | + | + | – | ||

| 
| 
| 
| 
| ||
min

| max

|
Заметим, что мы не внесли в первую строку таблицы значение аргумента 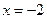 , так как оно не входит в
, так как оно не входит в  . Итак, получаем:
. Итак, получаем:  – точка минимума и
– точка минимума и  , а
, а  – точка максимума, причем
– точка максимума, причем 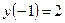 .
.
4) Рассмотрим функцию  .
.
-
 .
. -
 .
. -






 ,
,  – критические точки.
– критические точки. - Строим таблицу:
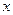
| 
| 
| 
| 
| 
| 
|

| + | – | – | + | ||

| 
| -4 | 
| 
| 
| |
max

| min

|
Итак,  – точка максимума и
– точка максимума и  ,
,  – точка минимума и
– точка минимума и  .
.
5) Рассмотрим функцию  .
.
-
 , так как логарифм существует только для положительных значений аргумента.
, так как логарифм существует только для положительных значений аргумента. -
 .
. -




 – критическая точка.
– критическая точка. - Строим таблицу:
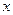
| 
| 
| |

| – | + | |

| 
| 
| 
|
min

|
Решение задачи №4
1) Функция  есть несократимая дробно-рациональная функция (т.е. ее числитель и знаменатель не имеют одинаковых корней). По теореме 21 из лекции 9 каждый корень
есть несократимая дробно-рациональная функция (т.е. ее числитель и знаменатель не имеют одинаковых корней). По теореме 21 из лекции 9 каждый корень  ее знаменателя порождает вертикальную асимптоту
ее знаменателя порождает вертикальную асимптоту  . Имеем:
. Имеем:  . Таким образом,
. Таким образом,  — вертикальная асимптота графика функции
— вертикальная асимптота графика функции  .
.
По той же теореме 21 правосторонние и левосторонние наклонные асимптоты дробно-рациональной функции совпадают и вычисляются по формуле  , где
, где  и
и  (формулы (29)-(30) в лекции 9). Имеем:
(формулы (29)-(30) в лекции 9). Имеем:
 ,
, 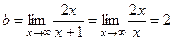 .
.
Таким образом,  — наклонная асимптота графика функции
— наклонная асимптота графика функции  (на самом деле эта асимптота является горизонтальной, так как прямая
(на самом деле эта асимптота является горизонтальной, так как прямая  параллельная оси
параллельная оси 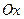 ).
).
2) Эта задача решается точно так же, как предыдущая. Приравниваем знаменатель рассматриваемой функции  к нулю:
к нулю:  Имеем две вертикальные асимптоты:
Имеем две вертикальные асимптоты:  и
и  .
.
Далее,  ,
,  . Таким образом, прямая
. Таким образом, прямая  (т.е. ось
(т.е. ось 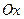 ) является наклонной (горизонтальной) асимптотой функции
) является наклонной (горизонтальной) асимптотой функции  .
.
3) Знаменатель функции  не имеет корней, поэтому эта функция не имеет вертикальных асимптот.
не имеет корней, поэтому эта функция не имеет вертикальных асимптот.
Найдем наклонную асимптоту. Имеем:
 ,
,  .
.
Получаем наклонную асимптоту  .
.
4) Функция  не является дробно-рациональной, поэтому нахождение ее вертикальных и наклонных асимптот следует производить непосредственно по формулам (28)–(30). Эта функция определена
не является дробно-рациональной, поэтому нахождение ее вертикальных и наклонных асимптот следует производить непосредственно по формулам (28)–(30). Эта функция определена  . Сначала будем искать вертикальные асимптоты. Имеем:
. Сначала будем искать вертикальные асимптоты. Имеем:
 , следовательно, по теореме 19 прямая
, следовательно, по теореме 19 прямая  является правосторонней вертикальной асимптотой;
является правосторонней вертикальной асимптотой;
 , следовательно, по теореме 19 прямая
, следовательно, по теореме 19 прямая  не является левосторонней вертикальной асимптотой.
не является левосторонней вертикальной асимптотой.
Теперь будем искать наклонные (правосторонние и левосторонние) асимптоты. Имеем:
 ,
,  , следовательно, по теореме 20 прямая
, следовательно, по теореме 20 прямая  является наклонной (горизонтальной) правосторонней асимптотой;
является наклонной (горизонтальной) правосторонней асимптотой;
 ,
, 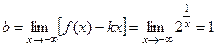 , следовательно, по теореме 20 прямая
, следовательно, по теореме 20 прямая  является наклонной (горизонтальной) левосторонней асимптотой.
является наклонной (горизонтальной) левосторонней асимптотой.
Решение задачи №5
Нахождение точек перегиба и интервалов выпуклости функции производится по той же схеме, что и нахождение точек локального экстремума и интервалов монотонности, только здесь вместо первой производной используется вторая производная (см. лекцию 10).
1) Рассмотрим функцию  .
.
·  .
.
·  .
.
·  .
.
· 



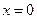 — точка, подозрительная на перегиб.
— точка, подозрительная на перегиб.
· Строим таблицу:
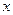
| 
| 
| |
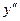
| – | + | |

| 
| 
| |
| перегиб |
Поясним построение таблицы. Ясно, что на интервале  выполняется неравенство
выполняется неравенство  , а на интервале
, а на интервале  — неравенство
— неравенство  . Поэтому по теореме 23 на первом интервале функция строго выпукла вверх, а на втором — строго выпукла вниз. Применяя теорему 26, получаем, что
. Поэтому по теореме 23 на первом интервале функция строго выпукла вверх, а на втором — строго выпукла вниз. Применяя теорему 26, получаем, что  — точка перегиба.
— точка перегиба.
2) Рассмотрим функцию 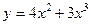 .
.
-
 .
. -
 .
. -
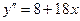 .
. -


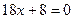

 — точка, подозрительная на перегиб.
— точка, подозрительная на перегиб. - Строим таблицу:
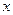
| 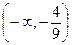
| 
| 
|
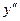
| – | + | |

| 
| 
| 
|
| перегиб |
3) Рассмотрим функцию  .
.
-
 .
. -
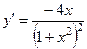 .
. -
 .
. -


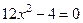



 ,
,  .
. - Строим таблицу:
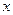
| 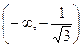
| 
| 
| 
| 
|
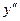
| + | – | + | ||

| 
| 
| 
| 
| 
|
| перегиб | перегиб |
Рассмотрим функцию.
-
 .
. -
 .
. -
 .
. -






 .
. - Составим таблицу:
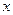
| 
| 
| 
|
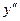
| – | + | |

| 
| 
| 
|
| перегиб |
Отметим, что для определения знака функции 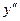 на интервале
на интервале  может быть взята точка
может быть взята точка  , а на интервале
, а на интервале  — точка
— точка  .
.
Решение задачи №6
Под полным исследованием функции и построением графика понимается следующая последовательность действий:
- нахождение
 — области определения функции;
— области определения функции; - определение интервалов возрастания и убывания и локальных экстремумов функции; построение соответствующих элементов графика;
- определение асимптот графика функции; построение ветвей графика, уходящих на бесконечность;
- исследование на выпуклость; уточнение поведения графика.
1) Рассмотрим функцию  .
.
-
 .
. - Определяем интервалы возрастания и убывания функции и экстремум функции:
 ;
; 



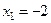 ,
, 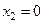 ,
, 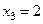 – критические точки.Составляем таблицу:
– критические точки.Составляем таблицу:
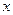
| 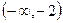
| –2 | 
| 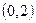
| 
| ||

| – | + | – | + | |||

| 
| 
| 
| 
| 
| 
| 
|
min

| max

| min

|
- Переходим к определению асимптот графика. Так как функция непрерывна на всей числовой оси, то вертикальных асимптот нет. По теореме 21 у многочлена степени выше первой наклонных асимптот также нет.
- Определим интервалы выпуклости и вогнутости графика функции и точки перегиба:
 ;
; 



 ,
,  –точки, подозрительные на перегиб.
–точки, подозрительные на перегиб.
Составляем таблицу:
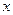
| 
| 
| 
| 
| 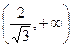
|
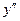
| + | – | + | ||

| 
| 
| 
| 
| 
|
| перегиб | перегиб |
- Построим теперь график функции:
2) Рассмотрим функцию  .
.
-
 .
. - Определяем интервалы возрастания и убывания функции и локальные экстремумы функции:
 ;
; 

 – критическая точка. Составим таблицу:
– критическая точка. Составим таблицу:
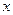
| 
| 
| 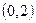
| 
| |

| + | + | – | – | |

|  
| –1 | 
|  
| |
max

|
- Переходим к определению асимптот графика. По теореме 21 вертикальные асимптоты порождаются корнями знаменателя дробно-рациональной функции. Таким образом,
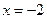 и
и  — вертикальные асимптоты графика функции
— вертикальные асимптоты графика функции  . Точно так же, как в пунктах 1) и 2) задачи №4, показывается, что наклонная асимптота имеет вид
. Точно так же, как в пунктах 1) и 2) задачи №4, показывается, что наклонная асимптота имеет вид  .
. - Определим интервалы выпуклости и точки перегиба:

 точек перегиба нет. Построим таблицу:
точек перегиба нет. Построим таблицу:
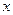
| 
| 
| 
|
| + | – | + |

| 
| 
| 
|
- Построим теперь график функции:
Решение задачи №7
Для того чтобы найти частную производную функции  по переменной
по переменной 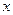 , фиксируем переменную
, фиксируем переменную  и дифференцируем
и дифференцируем  как функцию одной переменной
как функцию одной переменной 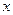 . Наоборот, для того чтобы найти частную производную функции
. Наоборот, для того чтобы найти частную производную функции  по переменной
по переменной  , фиксируем переменную
, фиксируем переменную 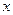 и дифференцируем
и дифференцируем  как функцию одной переменной
как функцию одной переменной  .
.
1)  .
.
Имеем:
 ; ;
|  . .
|
2) 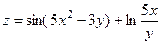 .
.
Имеем:
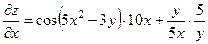 ; ;
|  . .
|
3) 
Имеем:
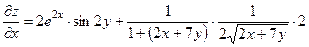 ; ;
|  . .
|
Решение задачи №8
Для того чтобы н






