ТЕОРИЯ ПРЕДЕЛОВ
И ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Раздел 2. Применение производных к исследованию функций
Курс лекций
и образец решения индивидуального задания
по высшей математике для бакалавров 1-го курса
очной формы обучения
Ростов-на-Дону
УДК 517(07)
Теория пределов и дифференциальное исчисление. Раздел 2. Применение производных к исследованию функций. Курс лекций и образец решения индивидуального задания для бакалавров 1-го курса очной формы обучения. – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 37 с.
Изложен курс лекций по применению производных к исследованию функций. Приведен образец решения индивидуального задания «Применение производных к исследованию функций».
Лекции 7 – 12 составлены И.В. Павловым. Образец решения индивидуального задания составлен О.В. Назарько и адаптирован к курсу лекций И.В.Павловым.
Предназначены для бакалавров 1-го курса очной формы, проходящих обучение на кафедре высшей математики РГСУ, а также на математических кафедрах других вузов.
Электронная версия находится в библиотеке, ауд. 224.
УДК 517(07)
| Составители: | д-р физ.-мат. наук, проф. И.В. Павлов, ассист. О.В. Назарько |
| Рецензенты: | канд. физ.-мат. наук, доц. А.М. Можаев, канд. физ.-мат. наук, доц. Г.А. Власков |
Редактор Т.М. Климчук
Доп. план 2011 г., поз. 180
Подписано в печать 12.07.11. Формат 60´84/16. Бумага писчая. Ризограф.
Уч.-изд.л. 3,2. Тираж 50 экз. Заказ 382
Редакционно-издательский центр
Ростовского государственного строительного университета
344022, Ростов-на-Дону, ул. Социалистическая, 162
© Ростовский государственный
строительный университет, 2011
ЧАСТЬ 2: ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
Лекция 7
Геометрический смысл производной. Уравнения
касательной и нормали к графику функции
Теорема 11. Пусть функция  непрерывна в точке
непрерывна в точке  . Тогда
. Тогда  дифференцируема в точке
дифференцируема в точке  в том и только в том случае, когда график данной функции имеет касательную в точке
в том и только в том случае, когда график данной функции имеет касательную в точке  , непараллельную оси Oy. При этом
, непараллельную оси Oy. При этом
 , ,
| (18) |
где  – угол наклона касательной по отношению к оси
– угол наклона касательной по отношению к оси  .
.
Доказательство. Построим чертеж:

|
Напомним, что касательной к кривой в точке A называется предельное положение секущей прямой AB, когда точка B, двигаясь по данной кривой, приближается к точке A (то есть расстояние  между точками A и B стремится к нулю).
между точками A и B стремится к нулю).
Предположим, что  строго, то есть x приближается к a по произвольной последовательности, строго стремящейся к a (см. определение 7). Имеем:
строго, то есть x приближается к a по произвольной последовательности, строго стремящейся к a (см. определение 7). Имеем:
 . .
| (19) |
Когда  ,
,  в силу непрерывности функции
в силу непрерывности функции  в точке
в точке  . Поэтому, если предельное положение
. Поэтому, если предельное положение  секущей AB существует, то отсюда следует, что
секущей AB существует, то отсюда следует, что 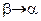 , причем
, причем  , так как по условию теоремы
, так как по условию теоремы  непараллельна Oy. Пользуясь непрерывностью функции тангенс, из (19) получаем (18).
непараллельна Oy. Пользуясь непрерывностью функции тангенс, из (19) получаем (18).
Обратно, если  существует, то из (19) следует существование конечного предела
существует, то из (19) следует существование конечного предела  . Из непрерывности функции арктангенс и из неравенства
. Из непрерывности функции арктангенс и из неравенства  вытекает, что предел
вытекает, что предел  существует и находится в интервале
существует и находится в интервале  . А это означает существование предельного положения
. А это означает существование предельного положения  секущей AB, причем
секущей AB, причем  непараллельна оси Oy.
непараллельна оси Oy.
| € |
Итак, равенство (18) показывает, что  , где k – угловой коэффициент касательной
, где k – угловой коэффициент касательной  . Применяя формулу (47) из лекций по линейной алгебре и аналитической геометрии (ЛЛААГ), получаем уравнение касательной
. Применяя формулу (47) из лекций по линейной алгебре и аналитической геометрии (ЛЛААГ), получаем уравнение касательной  :
:
 : :  . .
| (20) |
Используя соотношение между угловыми коэффициентами взаимно перпендикулярных прямых (см. формулу (52) из ЛЛААГ), получаем уравнение нормали n (то есть прямой, проходящей через точку касания A и перпендикулярной  ):
):
n:  . .
| (21) |
Понятие локального экстремума. Основные теоремы
дифференциального исчисления
Определение 14. Говорят, что в точке  функция
функция  имеет локальный максимум (соответственно, локальный минимум), если существует d-окрестность U точки a (см. определение 3), такая, что
имеет локальный максимум (соответственно, локальный минимум), если существует d-окрестность U точки a (см. определение 3), такая, что  (соответственно,
(соответственно,  ). Локальные максимумы и локальные минимумы называются локальными экстремумами.
). Локальные максимумы и локальные минимумы называются локальными экстремумами.
| € |

|
На представленном рисунке в точках  функция
функция  имеет локальный экстремум: в точках
имеет локальный экстремум: в точках  и
и  – локальный минимум, а в точках
– локальный минимум, а в точках  и
и  – локальный максимум. При этом во всех этих точках функция непрерывна, но только в одной точке
– локальный максимум. При этом во всех этих точках функция непрерывна, но только в одной точке  имеет конечную производную. Функция, представленная в примере 7, разрывна в точке
имеет конечную производную. Функция, представленная в примере 7, разрывна в точке  и имеет в этой точке локальный максимум.
и имеет в этой точке локальный максимум.
Следующая теорема, выражающая собой необходимый признак локального экстремума, позволит нам делать заключение о значении производной в точках локального экстремума.
Теорема 12 (теорема Ферма). Если в точке  функция
функция  дифференцируема и имеет локальный экстремум, то
дифференцируема и имеет локальный экстремум, то  .
.
Доказательство. Пусть, например, a – точка минимума. Если последовательность 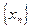 строго монотонно возрастает к a, то
строго монотонно возрастает к a, то  , а
, а  , значит
, значит  и по свойству 6 предела последовательности имеем:
и по свойству 6 предела последовательности имеем:
 . .
| (22) |
Аналогично, если 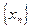 строго монотонно убывает к a, то
строго монотонно убывает к a, то  ,
,  и
и
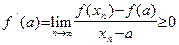 . .
| (23) |
Из неравенств (22) и (23) следует, что  .
.
| € |
Формула (20) дает следующую геометрическую интерпретацию теоремы Ферма: если в точке  функция
функция  дифференцируема, то она в этой точке имеет локальный экстремум тогда и только тогда, когда касательная, проведенная к графику функции
дифференцируема, то она в этой точке имеет локальный экстремум тогда и только тогда, когда касательная, проведенная к графику функции  в точке
в точке  , параллельна оси Ox. Читателю предлагается построить соответствующий рисунок.
, параллельна оси Ox. Читателю предлагается построить соответствующий рисунок.
Заметим, что условие  недостаточно для существования локального экстремума в точке
недостаточно для существования локального экстремума в точке  . Действительно, функция
. Действительно, функция 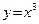 имеет в точке
имеет в точке 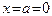 производную, равную нулю, однако при
производную, равную нулю, однако при  , а при
, а при 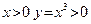 . Таким образом, определение 14 не выполняется. Читателю предлагается построить график функции
. Таким образом, определение 14 не выполняется. Читателю предлагается построить график функции 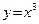 .
.
В дальнейшем нам понадобится следующая лемма, доказательство которой выходит за рамки нашей программы.
Лемма 5. Если функция  непрерывна на конечном замкнутом интервале
непрерывна на конечном замкнутом интервале  , то она ограничена на этом интервале, хотя бы в одной точке этого интервала принимает свое минимальное значение m и хотя бы в одной точке этого интервала принимает свое максимальное значение M.
, то она ограничена на этом интервале, хотя бы в одной точке этого интервала принимает свое минимальное значение m и хотя бы в одной точке этого интервала принимает свое максимальное значение M.
| € |
Теорема 13 (теорема Ролля). Пусть функция  непрерывна на конечном замкнутом интервале
непрерывна на конечном замкнутом интервале  , дифференцируема на интервале
, дифференцируема на интервале  и удовлетворяет условию
и удовлетворяет условию 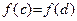 . Тогда существует хотя бы одна точка
. Тогда существует хотя бы одна точка  , такая, что
, такая, что  .
.

|
Доказательство. Если  на
на  , то в качестве a можно взять любую точку интервала
, то в качестве a можно взять любую точку интервала  . Пусть
. Пусть  . По лемме 5 в некоторой точке
. По лемме 5 в некоторой точке  функция
функция  принимает свое максимальное значение. Ясно, что в данном случае
принимает свое максимальное значение. Ясно, что в данном случае  и
и  . Поэтому
. Поэтому  . По теореме Ферма
. По теореме Ферма  .
.
Случай существования  рассматривается аналогично.
рассматривается аналогично.
| € |
Теорема 14 (теорема Коши). Пусть функции  и
и  непрерывны на конечном замкнутом интервале
непрерывны на конечном замкнутом интервале  и дифференцируемы на интервале
и дифференцируемы на интервале  . Тогда существует хотя бы одна точка
. Тогда существует хотя бы одна точка  , такая, что
, такая, что
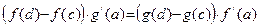 . .
| (24) |
Доказательство. Рассмотрим функцию  , заданную с помощью определителя:
, заданную с помощью определителя:
 . .
|
Очевидно,  непрерывна на
непрерывна на  , дифференцируема на
, дифференцируема на  и удовлетворяет условию
и удовлетворяет условию  (последнее вытекает из свойства 3 определителей; см. ЛЛААГ). По теореме Ролля существует хотя бы одна точка
(последнее вытекает из свойства 3 определителей; см. ЛЛААГ). По теореме Ролля существует хотя бы одна точка  , такая, что
, такая, что  . Раскладывая определитель по первой строке и производя дифференцирование, легко приводим последнее равенство к виду (24).
. Раскладывая определитель по первой строке и производя дифференцирование, легко приводим последнее равенство к виду (24).
| € |
Теорема 15 (теорема Лагранжа). Пусть функция  непрерывна на конечном замкнутом интервале
непрерывна на конечном замкнутом интервале  и дифференцируема на интервале
и дифференцируема на интервале  . Тогда существует хотя бы одна точка
. Тогда существует хотя бы одна точка  , такая, что
, такая, что
 . .
| (25) |
Доказательство. Доказательство немедленно следует из формулы (24), если положить  .
.
| € |

|
Интересен геометрический смысл теоремы Лагранжа. Для того, чтобы найти точку a, построим прямую CD (как показано на рисунке) и будем передвигать ее параллельно самой себе до тех пор, пока она не станет касательной к графику функции  в некоторой точке A. Абсцисса a точки A и будет точкой, удовлетворяющей равенству (25). Действительно,
в некоторой точке A. Абсцисса a точки A и будет точкой, удовлетворяющей равенству (25). Действительно,  .
.
Доказательство теоремы 9 (правила Лопиталя)
Доказательство проведем только для неопределенности типа  . Доопределяем, если это необходимо, функции
. Доопределяем, если это необходимо, функции  и
и  в точке
в точке  равенствами:
равенствами:  . Тогда из условий 1) данной теоремы следует, что эти функции непрерывны в точке
. Тогда из условий 1) данной теоремы следует, что эти функции непрерывны в точке  .
.
Предположим сначала, что  , строго монотонно убывая. Так как функция
, строго монотонно убывая. Так как функция  на интервале
на интервале  удовлетворяет условиям теоремы Лагранжа, то существует
удовлетворяет условиям теоремы Лагранжа, то существует  , такое, что
, такое, что 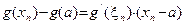 . Но из условий теоремы 9 следует, что
. Но из условий теоремы 9 следует, что  при достаточно больших n. Следовательно при тех же n
при достаточно больших n. Следовательно при тех же n  . Имеем:
. Имеем:
 . .
| (26) |
Так как функции  и
и  на интервале
на интервале  удовлетворяют условиям теоремы Коши, то существует
удовлетворяют условиям теоремы Коши, то существует  , такое, что
, такое, что  , а поскольку
, а поскольку  , то
, то  . Подставляя это в (26), получаем:
. Подставляя это в (26), получаем:
 . .
|
Но очевидно, что  строго. Поэтому, применяя условие 2) данной теоремы, получаем, что последний предел равняется b. То есть
строго. Поэтому, применяя условие 2) данной теоремы, получаем, что последний предел равняется b. То есть  , а это означает, что
, а это означает, что  .
.
Аналогично доказывается, что 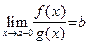 . По теореме 2
. По теореме 2  .
.
| € |
Заметим, что из существования предела  в общем случае не следует существование предела
в общем случае не следует существование предела  . Рассмотрим, например, функции
. Рассмотрим, например, функции  и
и  . Ясно, что эти функции дифференцируемы при
. Ясно, что эти функции дифференцируемы при  и
и  . Далее, так как
. Далее, так как  , а
, а  при
при  , то по свойству 8 предела функции
, то по свойству 8 предела функции  . Очевидно также, что
. Очевидно также, что  . Имеем
. Имеем 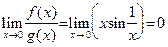 опять же по свойству 8 предела функции. Однако
опять же по свойству 8 предела функции. Однако  , а последний предел не существует, поскольку
, а последний предел не существует, поскольку  , а
, а  не существует (действительно, если взять последовательность
не существует (действительно, если взять последовательность  , то
, то  , то есть нечетные члены полученной последовательности равны –1, а четные равны +1; ср. с пунктом 2) примера 2).
, то есть нечетные члены полученной последовательности равны –1, а четные равны +1; ср. с пунктом 2) примера 2).
ЧАСТЬ 2: ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
Лекция 8
Исследование на монотонность и нахождение экстремумов функций
Определение 15. Пусть J – некоторый интервал на действительной прямой. Говорят, что функция  монотонно возрастает (соответственно, строго монотонно возрастает) на J, если
монотонно возрастает (соответственно, строго монотонно возрастает) на J, если  , таких, что
, таких, что  , выполняется неравенство:
, выполняется неравенство:
 (соотв., (соотв.,  ). ).
| (27) |
Если неравенства в (27) заменить на противоположные, то получаем определение монотонно убывающей (соотв., строго монотонно убывающей) функции.
| € |
Теорема 16 (критерий монотонности). Пусть функция  дифференцируема на открытом интервале
дифференцируема на открытом интервале  .
.
1)  монотонно возрастает на
монотонно возрастает на  тогда и только тогда, когда
тогда и только тогда, когда  .
.
2)  монотонно убывает на
монотонно убывает на  тогда и только тогда, когда
тогда и только тогда, когда  .
.
Доказательство. Докажем лишь пункт 1) (пункт 2) доказывается аналогично). Если  монотонно возрастает на
монотонно возрастает на  , то, заменив в доказательстве теоремы Ферма (теорема 12) a на x и проводя рассуждения по той же схеме, без труда получаем неравенство
, то, заменив в доказательстве теоремы Ферма (теорема 12) a на x и проводя рассуждения по той же схеме, без труда получаем неравенство 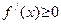 .
.

|
Обратно, пусть  и
и  такие, что
такие, что  . По теореме Лагранжа (теорема 15) существует точка
. По теореме Лагранжа (теорема 15) существует точка  , такая, что
, такая, что 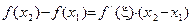 . Так как
. Так как  , то из полученного равенства следует
, то из полученного равенства следует 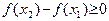 , или
, или 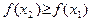 .
.
| € |
Пример 20. Рассмотрим функцию  . Так как
. Так как  , то из теоремы 16 следует, что эта функция монотонно возрастает на всей действительной прямой. Легко видеть, что на самом деле
, то из теоремы 16 следует, что эта функция монотонно возрастает на всей действительной прямой. Легко видеть, что на самом деле  строго монотонно возрастает на
строго монотонно возрастает на  (докажите это!). При этом, однако,
(докажите это!). При этом, однако,  .
.
| € |
Пример 20 показывает, что в полном объеме аналог теоремы 16 не может быть сформулирован для строго монотонных функций. Однако справедлива следующая теорема, доказательство которой дословно повторяет вторую часть доказательства теоремы 16.
Теорема 17. Пусть функция  дифференцируема на открытом интервале
дифференцируема на открытом интервале  .
.
1) Если 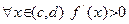 , то
, то  строго монотонно возрастает на
строго монотонно возрастает на  .
.
2) Если  , то
, то  строго монотонно убывает на
строго монотонно убывает на  .
.
| € |
Определение 16. Точка  называется критической точкой функции
называется критической точкой функции  , если удовлетворяется одно из следующих трех условий:
, если удовлетворяется одно из следующих трех условий:
1) точка  стационарна, то есть
стационарна, то есть  (см. теорему 12);
(см. теорему 12);
2) в точке  производная
производная  не существует, однако функция
не существует, однако функция  непрерывна в этой точке;
непрерывна в этой точке;
3) функция  имеет разрыв в точке
имеет разрыв в точке  .
.
| € |
Принимая во внимание теорему Ферма, легко видеть, что если функция имеет локальный экстремум в точке  , то эта точка является критической. Обратное неверно ни в одном из случаев, перечисленных в определении 16. Читателю предлагается построить соответствующие графики.
, то эта точка является критической. Обратное неверно ни в одном из случаев, перечисленных в определении 16. Читателю предлагается построить соответствующие графики.
Определение 17. Будем говорить, что функция  меняет знак (соответственно, не меняет знака) при переходе через точку
меняет знак (соответственно, не меняет знака) при переходе через точку  , если она определена в некоторой d-окрестности точки a (за исключением, быть может, самой точки a), сохраняет знак на интервале
, если она определена в некоторой d-окрестности точки a (за исключением, быть может, самой точки a), сохраняет знак на интервале  и на интервале
и на интервале  и знаки функции
и знаки функции  на этих интервалах различны (соотв., одинаковы). ›
на этих интервалах различны (соотв., одинаковы). ›
Теорема 18 (достаточное условие экстремума). Пусть функция  непрерывна в точке
непрерывна в точке  . Если при переходе через эту точку производная
. Если при переходе через эту точку производная 
1) меняет знак "+" на "–", то  – точка локального максимума;
– точка локального максимума;
2) меняет знак "–" на "+", то  – точка локального минимума;
– точка локального минимума;
3) не меняет знака, то  не является точкой локального экстремума.
не является точкой локального экстремума.
Доказательство. 1) Пусть  , последовательность
, последовательность 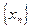 строго монотонно возрастает к a и
строго монотонно возрастает к a и  . Так как на
. Так как на  производная данной функции положительна, то по теореме 16
производная данной функции положительна, то по теореме 16  для
для  .Применяя свойство 6 предела последовательности и непрерывность функции в точке a, получаем:
.Применяя свойство 6 предела последовательности и непрерывность функции в точке a, получаем:  . Аналогично, для
. Аналогично, для  также получаем
также получаем  . Остается принять во внимание определение 14.
. Остается принять во внимание определение 14.
Пункт 2) доказывается точно так же, как пункт 1).
Докажем 3). Пусть производная до точки a и после точки a имеет знак "+". Рассуждая, как в пункте 1), получаем  при
при  и
и  при
при  . Если бы в точке
. Если бы в точке  был экстремум (например, максимум), то существовала бы такая точка
был экстремум (например, максимум), то существовала бы такая точка  , что
, что  при
при  . Следовательно,
. Следовательно, 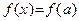 при
при  , Что противоречит (в силу теоремы 17) строго монотонному возрастанию функции на
, Что противоречит (в силу теоремы 17) строго монотонному возрастанию функции на  . Полученное противоречие доказывает, что экстремума в точке
. Полученное противоречие доказывает, что экстремума в точке  нет.
нет.
| € |
Пример 21. Найдем интервалы монотонности и точки локального экстремума функции  . Очевидно, D(y)
. Очевидно, D(y)  . Находим производную и затем приравниваем ее к нулю, чтобы найти критические точки:
. Находим производную и затем приравниваем ее к нулю, чтобы найти критические точки:  ;
;  . Теперь, применяя известный из школьного курса "метод интервалов", заполним таблицу:
. Теперь, применяя известный из школьного курса "метод интервалов", заполним таблицу:

| 
| –3 | (–3,2) | 
| |

| + | – | + | ||

| 
| 
| 
| 
| 
|
max

|  min
min
| ||||
Напомним, что в первой строке таблицы расписывается область определения функции, раздробленная на интервалы критическими точками. Во второй строке с помощью "пробных точек" вычисляются знаки производных на интервалах дробления. Действительно, если производная непрерывна вне критических точек, то она сохраняет знак на каждом интервале дробления. Поэтому для определения этого знака, достаточно вычислить знак в произвольно взятой "пробной точке" интервала. Например, чтобы вычислить знак производной на интервале  , достаточно взять, скажем, точку
, достаточно взять, скажем, точку  , подставить ее в выражение
, подставить ее в выражение  и определить знак числа
и определить знак числа 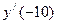 . Очевидно, это знак " + ". Точно так же вычисляются знаки производной на остальных интервалах. Ниже точек –3 и 2 ставим число 0, равное значению производной в этих точках.
. Очевидно, это знак " + ". Точно так же вычисляются знаки производной на остальных интервалах. Ниже точек –3 и 2 ставим число 0, равное значению производной в этих точках.
В третьей строке, опираясь на теорему 17, стрелками указываем характер монотонности функции на каждом интервале, а также записываем значения функций в критических точках. Ниже этих значений, применяя теорему 18, отмечаем наличие или отсутствие локального экстремума, а также в виде куска графика отображаем поведение функции в окрестности критической точки.
| € |
Пример 22. Найдем интервалы монотонности и точки локального экстремума функции  . Имеем: D(y)
. Имеем: D(y)  и
и  =
=
 . Далее,
. Далее,  (заметим, что
(заметим, что 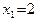 – кратный корень). Построим таблицу:
– кратный корень). Построим таблицу:

| 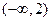
| (2,3) | (3,5) | 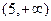
| ||

| + | + | – | + | ||

| 
| 
| 
| 
| 
| |
 нет extr
нет extr
|  min
min
|
Заметим, что мы не внесли в таблицу значение аргумента  , так как оно не входит в D(y) и, следовательно, бессмысленно говорить об экстремуме в этой точке.
, так как оно не входит в D(y) и, следовательно, бессмысленно говорить об экстремуме в этой точке.
| € |
Пример 23. Найдем интервалы монотонности и точки локального экстремума функции  . Имеем: D(y)
. Имеем: D(y)  и
и  . Далее,
. Далее, 
 (
( – двукратный корень). Составим таблицу:
– двукратный корень). Составим таблицу:

| 
| (0,3) | 
| |||

| + | + | – | |||

| 
| 
| 
| 
| ||
 нет extr
нет extr
| max

| |||||
| € | ||||||
Заметим, что в примерах 22 и 23 именно двукратные корни производной являлись критическими точками, но не экстремумами соответствующих функций. Легко доказать, что если производная непрерывна и ее корень имеет четную кратность, то он не является точкой экстремума исследуемой функции.
Пример 24. Найдем интервалы монотонности и точки локального экстремума функции  . Имеем D(y)
. Имеем D(y)  , однако можно доказать, что в точке
, однако можно доказать, что в точке  производная
производная  не существует (здесь сказывается неблагоприятное влияние члена
не существует (здесь сказывается неблагоприятное влияние члена  ). Нетрудно также видеть, что
). Нетрудно также видеть, что  не существует в точке
не существует в точке  (можно сказать, что в этой точке производная равна бесконечности). Если
(можно сказать, что в этой точке производная равна бесконечности). Если 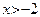 , то
, то  ,
,  и
и  . Если же
. Если же  , то
, то 
 и
и  . Однако этот корень не принадлежит рассматриваемому интервалу и поэтому должен быть отброшен. Итак, мы получили три критические точки (см. определение 15): точки
. Однако этот корень не принадлежит рассматриваемому интервалу и поэтому должен быть отброшен. Итак, мы получили три критические точки (см. определение 15): точки 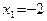 и
и  , в которых функция непрерывна, но производная не существует, и стационарную точку
, в которых функция непрерывна, но производная не существует, и стационарную точку  .
.

| 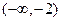
| –2 | (–2,–1) | –1 | (–1,0) | 
| |||

| – | не сущ. | + | – | не сущ. | + | |||

| 
| 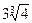
| 
| 
| 
| ||||
 min
min
| max

|  min
min
| |||||||
| € | |||||||||
Пример 25. Найдем интервалы монотонности и точки локального экстремума функции 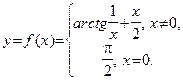 . Ясно, что D(y)
. Ясно, что D(y)  . Для того, чтобы выяснить, является ли данная функция непрерывной в точке
. Для того, чтобы выяснить, является ли данная функция непрерывной в точке  , вычислим ее левый и правый предел при
, вычислим ее левый и правый предел при 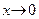 . Имеем:
. Имеем:  (см. пункт 6) теоремы 8). Однако, по той же теореме
(см. пункт 6) теоремы 8). Однако, по той же теореме  . Поэтому
. Поэтому  – точка разрыва данной функции и производной в этой точке у нее нет. При
– точка разрыва данной функции и производной в этой точке у нее нет. При  :
:
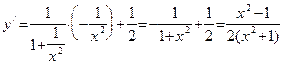 и
и  . Итак, мы получили три критические точки (см. определение 15): стационарные точки
. Итак, мы получили три критические точки (см. определение 15): стационарные точки  и
и 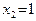 и точку разрыва функции
и точку разрыва функции  . Построим таблицу:
. Построим таблицу:

| 
| –1 | (–1,–0) | (0,1) | 
| ||

| + | – | не сущ. | – | + | ||

| 
| 
| 
| 
| 
| 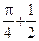
| 
|
max

|  max
max
|  min
min
|
Так как точка  не подпала под условия теоремы 18, то мы получили нужный нам вывод с учетом вычисленных левого и правого предела. ›
не подпала под условия теоремы 18, то мы получили нужный нам вывод с учетом вычисленных левого и правого предела. ›






